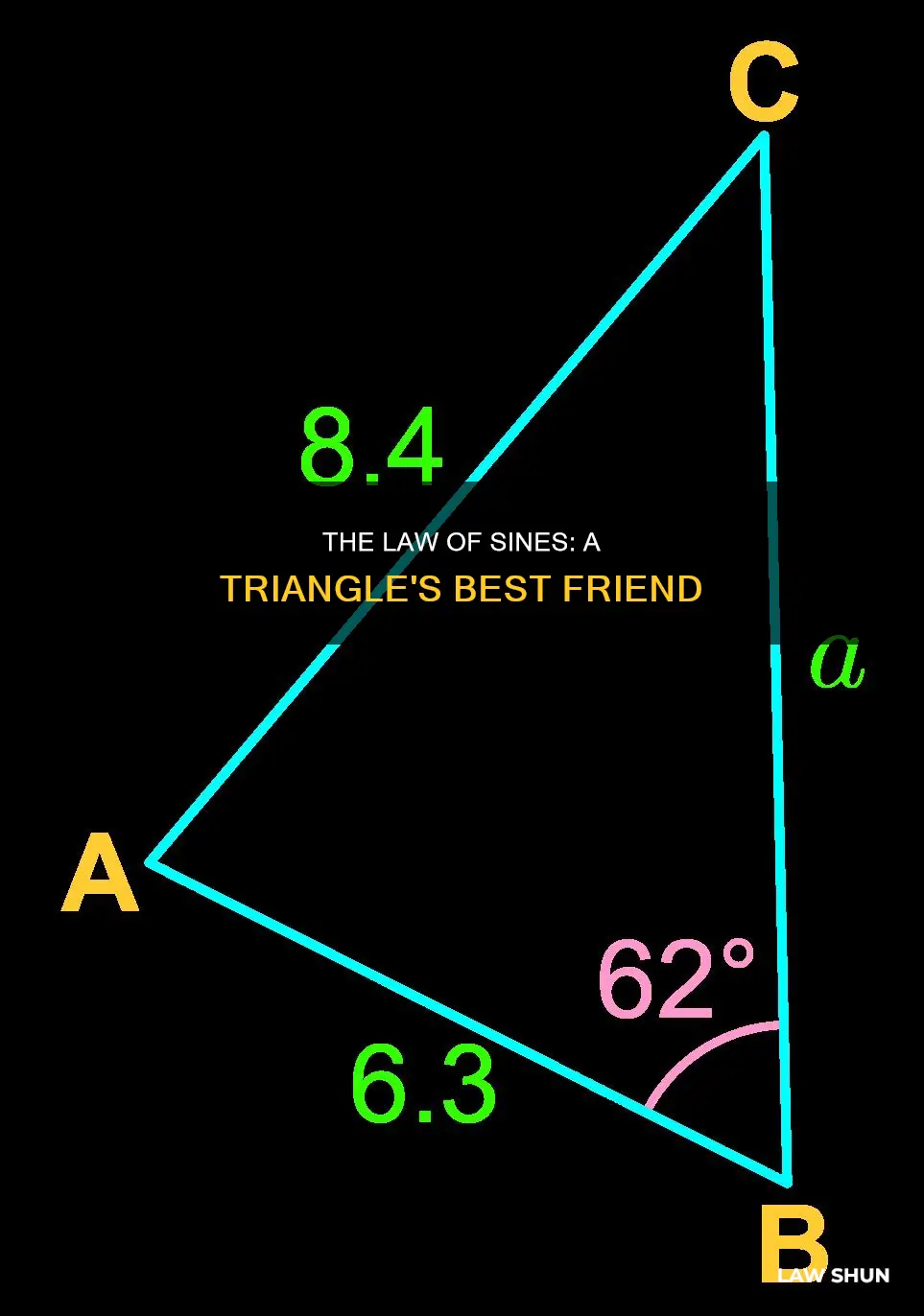
The law of sines, also known as the sine rule, is a trigonometric equation that can be used to find unknown sides and angles in triangles. The law of sines states that the ratio of the length of a side of a triangle to the sine of its opposite angle is the same for all three sides. This law can be used to solve for sides and angles in any triangle, not just right triangles, and is particularly useful when two angles and a side are known, or when two sides and a non-included angle are known. The law of sines can also be generalized to higher dimensions on surfaces with constant curvature. However, in some cases, the triangle may not be uniquely determined, resulting in two possible values for the enclosed angle.
| Characteristics | Values |
|---|---|
| Definition | The law of sines, also known as the sine rule, sine law, or sine formula, is an equation relating the lengths of the sides of any triangle to the sines of its angles. |
| Formula | \({\displaystyle {\frac {a}{\sin {\alpha }}}\,=\,{\frac {b}{\sin {\beta }}}\,=\,{\frac {c}{\sin {\gamma }}}\,=\,2R}\) or ${\displaystyle {\frac {\sin {\alpha }}},=,{\frac {\sin {\beta }}},=,{\frac {\sin {\gamma }}}} |
| Application | Used to find unknown sides or angles of a triangle, especially in engineering, astronomy, and navigation. |
| Requirements | At least two angles and their respective side measurements or two sides and the angle opposite them. |
| Ambiguity | In some cases, the data may lead to two possible values for the enclosed angle, resulting in two separate triangles. |
What You'll Learn
- The law of sines can be used to find unknown sides of a triangle
- It can also be used to find unknown angles
- The law of sines is used in engineering to measure the angle of tilt
- It is also used in astronomy to measure the distance between planets or stars
- The sine rule can be used in any triangle, not just right-angled triangles

The law of sines can be used to find unknown sides of a triangle
The law of sines, also known as the sine rule, is a trigonometric equation that can be used to find the unknown sides of a triangle. It is defined as the ratio of the side length of a triangle to the sine of its opposite angle, which is the same for all three sides. In other words, the law of sines states that the sides of a triangle are proportional to the sines of their opposite angles. This law can be applied to any triangle, not just right triangles, and is particularly useful when two angles and a side are known, or when two sides and a non-enclosed angle are known.
The law of sines is represented by the equation:
>
Where a, b, and c are the lengths of the sides of a triangle, and α, β, and γ are the opposite angles. R represents the radius of the triangle's circumcircle.
By using the law of sines, we can solve for unknown sides of a triangle. For example, if we know the length of side a and the measure of angle A, we can calculate the "law of sines" ratio, or simply the sine of angle A. This ratio can then be used to find the other sides of the triangle. It's important to note that the law of sines may result in ambiguous cases, where two separate triangles can be constructed from the given data, leading to two possible solutions.
The law of sines has various applications in engineering, astronomy, and navigation. It is a valuable tool in trigonometry, enabling us to solve triangles and find unknown side lengths or angles.
Crushing Cans: Gas Laws in Action
You may want to see also

It can also be used to find unknown angles
The law of sines, also known as the sine rule, is a trigonometric equation that can be used to find unknown angles or sides of a triangle. It is applicable to all triangles, not just right-angled triangles, and states that the ratio of the side length of a triangle to the sine of the opposite angle is the same for all three sides.
The law of sines can be used to find an unknown angle when the lengths of the sides of the triangle are known. This is done by using the formula:
> a/sin α = b/sin β = c/sin γ
Where a, b, and c are the lengths of the sides of the triangle, and α, β, and γ are the opposite angles.
For example, if we know the lengths of two sides of a triangle, and the angle opposite one of those sides, we can use the law of sines to find the measure of the unknown angle. Let's say we have a triangle with sides AB = c, BC = a, and AC = b, and we know that angle ABC = 45 degrees. We can use the law of sines to find the measure of the unknown angle, angle BAC. Substituting the given information into the formula, we get:
> sin(ABC)/c = sin(BAC)/b
Now, we can solve for the unknown angle, BAC, by inputting the values into a calculator.
The law of sines can also be used to find unknown angles when two angles and one side are known, or when two sides and one non-enclosed angle are known. In some cases, the triangle may not be uniquely determined by the given data, resulting in an ambiguous case with two possible solutions.
The States' Power: Creating Their Own Felony Laws
You may want to see also

The law of sines is used in engineering to measure the angle of tilt
The law of sines is a trigonometric equation that relates the lengths of a triangle's sides to the sines of its angles. It is also known as the sine rule, sine law, or sine formula. The law of sines is defined as the ratio of the length of a triangle's side to the sine of the angle created by the remaining two sides. This ratio is the same for all three sides of a triangle, regardless of their sides and angles.
To use the law of sines, at least two angles and their respective side measurements are required. It is often employed when two angles and one side, or two angles and one included side, are known. This is referred to as the ASA (angle-side-angle) or AAS (angle-angle-side) criteria. The formula for the law of sines is:
> a/sin A = b/sin B = c/sin C
Where a, b, and c are the lengths of the triangle's sides, and A, B, and C are the triangle's angles. By applying this formula, engineers can calculate the unknown angle of tilt, as long as they have the necessary measurements.
It is important to note that in some cases, the triangle may not be uniquely determined by the given data, resulting in an ambiguous case. In these situations, there could be two possible values for the enclosed angle, and additional information or considerations may be needed to determine the unique solution.
Sponsoring Parents-in-Law: A US Citizen's Guide
You may want to see also

It is also used in astronomy to measure the distance between planets or stars
The law of sines, also known as the sine rule, is a trigonometric equation relating the lengths of the sides of any triangle to the sines of its angles. The law of sines can be used to find the unknown angle or side of an oblique triangle (any triangle that is not a right triangle). It is defined as the ratio of side length to the sine of the opposite angle and holds for all three sides of a triangle, regardless of their sides and angles.
The law of sines is also used in astronomy to measure the distance between planets or stars. This application of the law of sines is rooted in the work of ancient astronomers. For example, the 2nd-century Hellenistic astronomer Ptolemy used an equivalent of the law of sines in his work, the 'Almagest'. Brahmagupta, a 7th-century Indian mathematician, expressed the circumradius of a triangle as the product of two sides divided by twice the altitude in his work, 'Brāhmasphuṭasiddhānta'. In another work, 'Khaṇḍakhādyaka', Brahmagupta presented a method for finding the distance between the Earth and a planet following an epicycle, demonstrating the versatility of the law of sines in astronomy.
The law of sines is particularly useful in astronomy when dealing with triangles on a sphere, where the sides are arcs of great circles. This is known as the spherical law of sines. By considering a unit sphere with three unit vectors drawn from the origin to the vertices of the triangle, the angles and sides of the triangle can be determined.
In ancient times, astronomers like the Babylonians kept detailed records of the motion of the planets, enabling them to predict solar and lunar eclipses. This work required a deep understanding of angular distances measured on the celestial sphere. As a result, they invented techniques that later became part of spherical trigonometry, including the law of sines.
Social Contracts: Legally Binding?
You may want to see also

The sine rule can be used in any triangle, not just right-angled triangles
The sine rule, also known as the law of sines, is a trigonometric equation relating the lengths of the sides of a triangle to the sines of its angles. It is used to find the unknown sides or angles of a triangle. The law of sines is not limited to right-angled triangles and can be applied to any triangle, including scalene and oblique triangles.
The sine rule is defined as the ratio of the side length of a triangle to the sine of its opposite angle, which is consistent across all three sides of the triangle. In other words, for sides a, b, and c, and their respective opposite angles A, B, and C, the equation can be written as:
> {"\displaystyle {"\frac {a}{\sin {\alpha }}}\,=\,{\frac {b}{\sin {\beta }}}\,=\,{\frac {c}{\sin {\gamma }}}}}
This equation can be manipulated by taking the reciprocal of each fraction, resulting in:
> {"\displaystyle {"\frac {\sin {\alpha }}{a}}\,=\,{\frac {\sin {\beta }}{b}}\,=\,{\frac {\sin {\gamma }}{c}}}}
The sine rule is particularly useful when specific sets of measurements of a triangle are known. For example, it can be used when two angles and one side are known, or when two sides and one non-enclosed angle are given. This technique is known as triangulation.
The law of sines is a valuable tool in various fields, including engineering, astronomy, and navigation. It is one of the primary tools for solving triangles, alongside the law of cosines, and can be generalized to higher dimensions on surfaces with constant curvature.
Family Law Attorneys: Credit Card Payment Options
You may want to see also
Frequently asked questions
The law of sines, also known as the sine rule, is an equation that relates the lengths of the sides of any triangle to the sines of its angles.
The law of sines can be used to find the sides of a triangle when two angles and one side are known. It can also be used when two sides and one non-enclosed angle are known.
The formula for the law of sines is:
> {\displaystyle {\frac {a}{\sin {\alpha }}}\,=\,{\frac {b}{\sin {\beta }}}\,=\,{\frac {c}{\sin {\gamma }}}\,=\,2R},
where a, b, and c are the lengths of the sides of a triangle, and α, β, and γ are the opposite angles, while R is the radius of the triangle's circumcircle.







