The law of sines, also known as the sine rule, is used to determine the unknown side of a triangle when two angles and sides are given. It is a trigonometric function that can be used to find the unknown sides and angles of a triangle. The law of sines can be applied to right triangles, but it is more commonly used for non-right triangles or oblique triangles. In a right triangle, the Pythagorean theorem or SOHCAHTOA is typically used instead of the law of sines, as these methods are more straightforward for right triangles.
| Characteristics | Values |
|---|---|
| Definition | The law of sines is used to find the unknown angle or the side of a triangle. |
| Application | The law of sines is used in engineering to measure the angle of tilt. |
| Formula | The ratio of side length to the sine of the opposite angle. |
| General Formula | (a/sin A) = (b/sin B) = (c/sin C) |
| Other Formulas | Sin B/ Sin C= b / c; Sin A = a number and a = length |
| Other Names | Sine Rule, Sine Law, Sine Formula |
| Applicability | The law of sines is used for non-right triangles or oblique triangles. |
What You'll Learn
- The Law of Sines is used to find unknown angles or sides of a triangle
- The Law of Sines is also known as the Sine Rule
- The Sine Rule states that the ratio of the side length of a triangle to the sine of the opposite angle is the same for all three sides
- The Law of Sines can be used to find the unknown side of a triangle when two angles and sides are given
- The Law of Sines is used in engineering to measure the angle of tilt

The Law of Sines is used to find unknown angles or sides of a triangle
The Law of Sines, also known as the Sine Rule or Sine Law, is a formula used to determine unknown angles or sides of a triangle. It is defined as the ratio of the side length of a triangle to the sine of the opposite angle, which is the same for all three sides.
The formula for the Law of Sines is:
A/sin A) = (b/sin B) = (c/sin C)
Where a, b, and c are the sides of a triangle, and A, B, and C are the angles between the sides. This formula can be used to find an unknown side of a triangle when two angles and one side are known, or when two sides and one non-included angle are given.
The Law of Sines is typically used for oblique triangles, which are triangles that are not right triangles. It should be noted that the Law of Sines requires at least two angles and their respective side measurements to work.
In certain cases, the Law of Sines can also be used to find an unknown angle in a right triangle. However, it is worth noting that other methods, such as Pythagoras' theorem or SOHCAHTOA, may be more efficient for solving right triangles.
LLC for Law Firms in Texas: What You Need to Know
You may want to see also

The Law of Sines is also known as the Sine Rule
The Law of Sines, also known as the Sine Rule, is a trigonometric equation used to find the unknown sides or angles of a triangle. It is applicable to all triangles, including right triangles, and states that the ratio of the side length of a triangle to the sine of its opposite angle is the same for all three sides.
The Law of Sines can be expressed as:
> a/sin A = b/sin B = c/sin C
Where a, b, and c are the sides of a triangle, and A, B, and C are the angles between the sides. This formula allows us to solve for unknown sides or angles when we have two angles and one side or two angles and one included side.
The Law of Sines is particularly useful in triangulation, where it can be used to compute the remaining sides of a triangle when two angles and one side are known. It can also be applied when two sides and one non-enclosed angle are given. This versatility makes it a valuable tool in various fields, including engineering, where it is used to measure the angle of tilt.
The Law of Sines, or Sine Rule, has a long history, with early equivalents appearing in the work of 2nd-century astronomer Ptolemy and 7th-century Indian mathematician Brahmagupta. However, it was the 13th-century Persian mathematician Naṣīr al-Dīn al-Ṭūsī who stated and proved the planar law of sines, solidifying its place in trigonometry.
A Daughter-in-Law's Request: Mother-in-Law's Role
You may want to see also

The Sine Rule states that the ratio of the side length of a triangle to the sine of the opposite angle is the same for all three sides
The Sine Rule, also known as the Law of Sines, is a formula used to find the unknown side or angle of a triangle. It is particularly useful for solving non-right triangles, or "oblique triangles", which can be defined as any triangle that is not a right triangle.
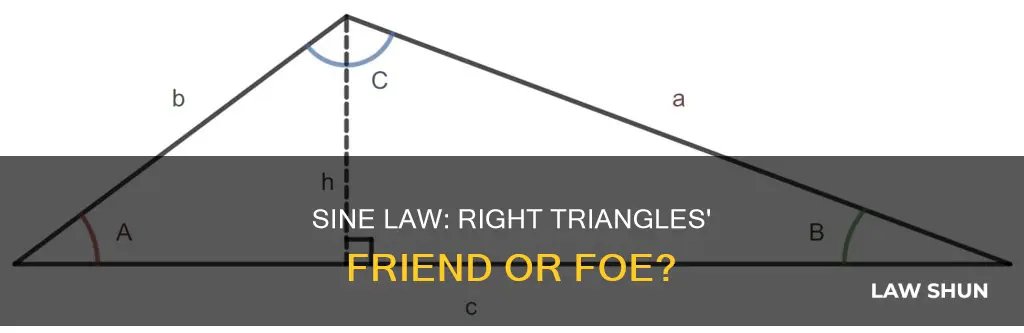
The rule states that the ratio of the side length of a triangle to the sine of the opposite angle is the same for all three sides. In other words, if we divide side 'a' by the sine of angle A, it will be equal to side 'b' divided by the sine of angle B, and also equal to side 'c' divided by the sine of angle C. This can be written as: a/sin A = b/sin B = c/sin C.
The Sine Rule can be used when we know two angles and one side, or two angles and one non-included side. This is known as the ASA (Angle-Side-Angle) or AAS (Angle-Angle-Side) criteria, and it will provide a unique solution.
The Sine Rule is useful because it allows us to turn non-right triangles into right triangles. This can be done by drawing a perpendicular line that divides the triangle into two right-angled triangles. The Sine Rule can then be applied to these new triangles to solve for unknown sides or angles.
Arizona Cops: Driving and Device Use Rules Explained
You may want to see also

The Law of Sines can be used to find the unknown side of a triangle when two angles and sides are given
The Law of Sines, also known as the Sine Rule, is a formula used to determine the unknown side or angle of a triangle. It is based on the ratio of the side length of a triangle to the sine of the opposite angle. This law is applicable to all three sides of a triangle, regardless of whether it is a right triangle or an oblique triangle.
The Law of Sines is particularly useful when certain combinations of measurements of a triangle are given. For example, it can be used when we know two angles and the included side (ASA criteria) or two angles and a non-included side (AAS criteria). In both cases, the law can be employed to find the unknown side of the triangle.
The formula for the Law of Sines is represented as:
A/sin A) = (b/sin B) = (c/sin C)
Where 'a', 'b', and 'c' are the sides of a triangle, and A, B, and C are the angles between the sides. By dividing side 'a' by the sine of angle A, we can determine the length of side 'b' by dividing it by the sine of angle B, and so on for any pair of angles and their opposite sides.
It is important to note that the Law of Sines can be applied to right triangles, but it is not the most efficient method as other theorems, such as Pythagoras' theorem, are more suitable for right triangles. However, in some cases, it may still be useful to apply the Law of Sines to a right triangle, especially when dealing with more complex problems or when working with programmatic perspectives.
Used Cars and Lemon Law: What You Need to Know
You may want to see also

The Law of Sines is used in engineering to measure the angle of tilt
The Law of Sines, also known as the Sine Rule, is a formula used to find the unknown side or angle of a triangle. It is defined as the ratio of side length to the sine of the opposite angle. The formula is given by (a/sin A) = (b/sin B) = (c/sin C). The law of sines is generally used when two angles and one side or two angles and one included side are given. This is known as the ASA (Angle-Side-Angle) and AAS (Angle-Angle-Side) criteria, respectively.
In addition to engineering, the Law of Sines has applications in astronomy and navigation. In astronomy, it is used to measure the distance between planets and stars. By knowing the angles and distances between celestial objects, astronomers can better understand the universe and our place in it. In navigation, the Law of Sines is used to determine distances and directions. For example, sailors have traditionally used the Law of Sines to navigate the seas, and today it is still used in aviation and maritime navigation.
The Law of Sines can also be applied to right triangles. In a right triangle, the Law of Sines can be used to find the unknown sides or angles, just like in any other triangle. However, in a right triangle, the sine function can be used in the usual way, and Pythagoras' theorem can also be applied. Therefore, while the Law of Sines is applicable to right triangles, it may be more common to use other methods, such as SOHCAHTOA or the Pythagorean theorem, as they may be more efficient or familiar.
Can States Challenge Federal Laws in the Supreme Court?
You may want to see also
Frequently asked questions
Yes, the law of sines can be used on right triangles.
The law of sines is used to find the unknown angle or the unknown side of a triangle.
The law of sines is represented by the equation: (a/sin A) = (b/sin B) = (c/sin C).
The law of sines is used to determine the unknown side of a triangle when two angles and sides are given.
While it is possible to use the law of sines on a right triangle, it is not the most efficient method. The Pythagorean theorem or SOHCAHTOA are often more effective for right triangles.