Unveiling Languages That Defy Zipf's Law: A Comprehensive Study

Zipf's law is an empirical law that states that when a list of measured values is sorted in decreasing order, the value of the n-th entry is often approximately inversely proportional to n. In the context of language, it means that the most common word in a text or corpus will occur approximately twice as often as the second most common word, three times as often as the third most common word, and so on. This law is named after the American linguist George Kingsley Zipf and is considered an important concept in quantitative linguistics.

While Zipf's law is found to apply to many languages, there are some languages and texts that deviate from this law. For example, in Spanish, the frequency of articles like el and la is much higher than would be expected based on Zipf's law. Additionally, certain literary works, such as James Joyce's Finnegans Wake, which uses a lot of rare and made-up words, also deviate from the law.

Even within a single language, there can be variations in how closely different texts adhere to Zipf's law. For instance, in English, the Brown Corpus of American English text closely follows Zipf's law, with the word the being the most common and occurring nearly twice as often as the second-place word of. However, a corpus of 30,000 English texts showed that only about 15% of them had a good fit to Zipf's law, with slight changes in the definition increasing this percentage to nearly 50%.

So, while Zipf's law is a useful concept in linguistics, it is important to recognize that it is not an exact rule and that there can be deviations and variations depending on the language, text, author, topic, and other factors.

Zipf's Law applies to almost all languages

Zipf's law is an empirical law stating that when a list of measured values is sorted in decreasing order, the value of the n-th entry is often approximately inversely proportional to n. In the context of language, Zipf's law states that the most common word in a text or corpus of natural language will occur approximately twice as often as the second most common word, three times as often as the third most common word, and so on.

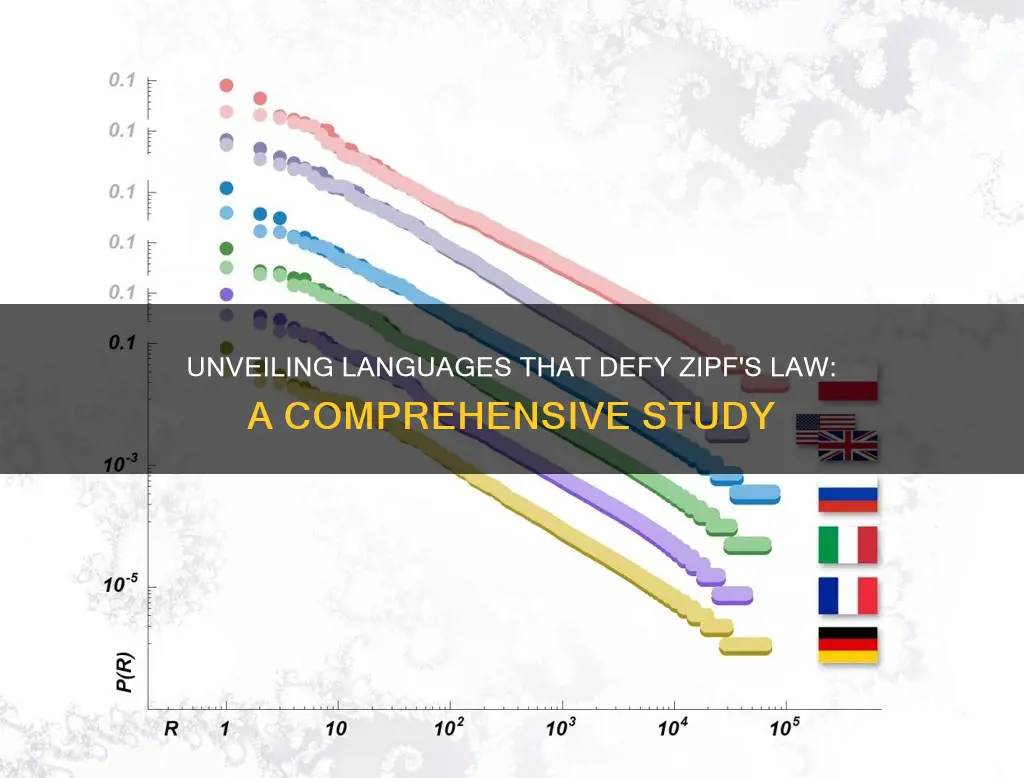
Despite some debate about whether it is a universal law or a statistical artifact, Zipf's law appears to apply to almost all languages. It has been found to hold for the first 10 million words in 30 different languages on Wikipedia, including English, Hindi, French, Mandarin, and Spanish. Even languages that have not yet been deciphered, such as the Voynich Manuscript, appear to follow Zipf's law.

Zipf's law also applies to individual texts if they are large enough. For example, it has been found to apply fairly neatly to Charles Darwin's "On the Origin of Species" and even Shakespeare's "Hamlet".

There are several potential explanations for why Zipf's law seems to apply to almost all languages. One idea is that it arises from a balance of effort minimization, with speakers and writers using more frequently occurring words to minimize their effort, and listeners and readers seeking clarity from less frequently used words. Another explanation is that more common words become more popular over time as language spreads and develops, resulting in a snowball effect.

While Zipf's law is widely applicable, it is important to note that it is still an approximation. Some texts, such as Joyce's "Finnegan's Wake," deviate from the law due to the use of rare and made-up words. Additionally, Zipf's law is typically applied to corpora rather than entire languages, as it is challenging to obtain a comprehensive sample of all utterances in a language.

The law also applies to languages that haven't been deciphered yet

Zipf's law, an empirical law, states that when a list of measured values is sorted in decreasing order, the value of the n-th entry is often approximately inversely proportional to n. In the context of language, it relates to the frequency of a word being a power law function of its frequency rank.

The law is named after the American linguist George Kingsley Zipf, and it holds true for almost all languages, including those that have not been deciphered yet, such as the Voynich Manuscript. This mysterious document, carbon-dated to the 15th century, has been found to follow Zipf's law, despite the fact that the underlying language remains unknown.

The applicability of Zipf's law to undeciphered languages is intriguing, as it suggests that certain mathematical principles may underlie human language, regardless of its specific form. This regularity extends beyond just the frequency of individual words, as Zipf's law has also been found to hold for phrases in various languages.

While the exact reasons for the prevalence of Zipf's law in language are not fully understood, several theories have been proposed. One idea is that it arises from a balance of effort minimization, with speakers and listeners/readers seeking to optimize their communication by using more frequently occurring words. Another theory suggests that common words become more popular over time, resulting in a snowball effect that leads to the observed distribution.

It is worth noting that Zipf's law is not universally applicable and that some sets of empirical data deviate from it. Additionally, the law has been found to hold for certain artificial languages, such as Esperanto and Toki Pona.

Zipf's Law is an empirical law

Zipf's law was named after the American linguist George Kingsley Zipf, who observed this relationship in natural language texts in 1932. However, Zipf did not claim to have discovered this phenomenon, and it had been previously observed by others such as the French stenographer Jean-Baptiste Estoup in 1916 and G. Dewey in 1923.

Zipf's law is not limited to language; it has been found to apply to various types of data in the physical and social sciences. For example, it describes the relationship between the population sizes of cities and their ranks when sorted in decreasing order. It also applies to corporate sizes, personal incomes, TV channel viewership, and more.

While Zipf's law is an empirical observation, the underlying mechanisms that give rise to this pattern are not well understood. One possible explanation is the principle of least effort, which suggests that speakers and listeners of a language aim to minimize their effort in communication, leading to the observed distribution of word frequencies. Another theory involves random text generation, where each character is chosen randomly from a uniform distribution of letters. In such texts, the "words" with different lengths tend to follow the macro-trend of Zipf's law, with shorter words being more probable and having equal probability.

It is worth noting that Zipf's law is an approximation and may not hold exactly for all languages or texts. Some sets of empirical data deviate from Zipf's law and are referred to as quasi-Zipfian. Additionally, the deviations from the ideal Zipf distribution may depend on various factors such as the language, the topic of the text, the author, translation, and spelling rules used.

The law is named after George Kingsley Zipf

Zipf's Law is named after George Kingsley Zipf, an American linguist and philologist who studied statistical occurrences in different languages. He earned his bachelor's, master's, and doctoral degrees from Harvard University, where he also served as chairman of the German department and university lecturer.

Zipf's Law, which he discovered in 1935, states that the frequency of a word is inversely proportional to its rank in the frequency table. In other words, the most frequent word will occur approximately twice as often as the second most frequent word, three times as often as the third most frequent word, and so on. This law appears to hold true across many different languages and even in texts from a single language.

Zipf initially intended his law as a model for linguistics, but he later generalized it to other disciplines. For example, he observed that the rank versus frequency distribution of individual incomes in a unified nation approximates this law. In his 1941 book, "National Unity and Disunity," he theorized that deviations from the normal curve of income distribution could signal social pressure for change or revolution.

In addition to his work in linguistics and sociology, Zipf also studied Chinese and demographics. His work has helped explain properties of the Internet, the distribution of income within nations, and many other collections of data.

The law is still an important concept in quantitative linguistics

Zipf's law is an empirical law that states that when a list of measured values is sorted in decreasing order, the value of the n-th entry is often approximately inversely proportional to n. In other words, the most common word in a text or corpus of natural language occurs approximately twice as often as the second most common one, three times as often as the third most common, and so on.

The law is named after the American linguist George Kingsley Zipf and is still an important concept in quantitative linguistics. It is considered a non-trivial property of human language, as it is unclear why words should follow such a precise mathematical rule.

Zipf's law has been found to hold for phrases, not just individual words. This reaffirms the law for language and calls for a re-evaluation of past and present word-based studies.

While Zipf's law is considered an approximation, it has been found to apply to almost all languages, including those that have not yet been deciphered, such as the Voynich Manuscript. It has also been found to apply to other types of data studied in the physical and social sciences, such as city populations, firm sizes, and family names.

The reason behind the universality of Zipf's law is still not well understood. One possible explanation is the principle of least effort, proposed by Zipf himself, which suggests that speakers and hearers of a language aim to minimize their effort to reach understanding, leading to the observed Zipf distribution. Another explanation involves random text generation, where in a document with characters chosen randomly, the "words" with different lengths follow the macro-trend of Zipf's law.

In summary, Zipf's law remains an important concept in quantitative linguistics due to its universality across languages and its applicability to phrases, not just individual words. While the exact reason for its occurrence is still unknown, several theories have been proposed, and the law continues to be a subject of research and discussion in the field of linguistics.

Frequently asked questions