Hooke's Law, also known as the law of elasticity, was formulated by English scientist Robert Hooke in the 17th century. It states that the force required to extend or compress a spring is directly proportional to the distance of that extension or compression. This principle can be applied to any elastic object, including springs, rubber bands, and even the human lung.
| Characteristics | Values |
|---|---|
| Named After | 17th-century British physicist Robert Hooke |
| First Stated | 1660, as a Latin anagram |
| Published Solution | 1678, as "ut tensio, sic vis" ("as the extension, so the force" or "the extension is proportional to the force") |
| Application | Applicable to any elastic object of arbitrary complexity, as long as a single number can express the deformation and the stress |
| Stress-Strain Relationship | For small deformations, the stress and strain are proportional to each other |
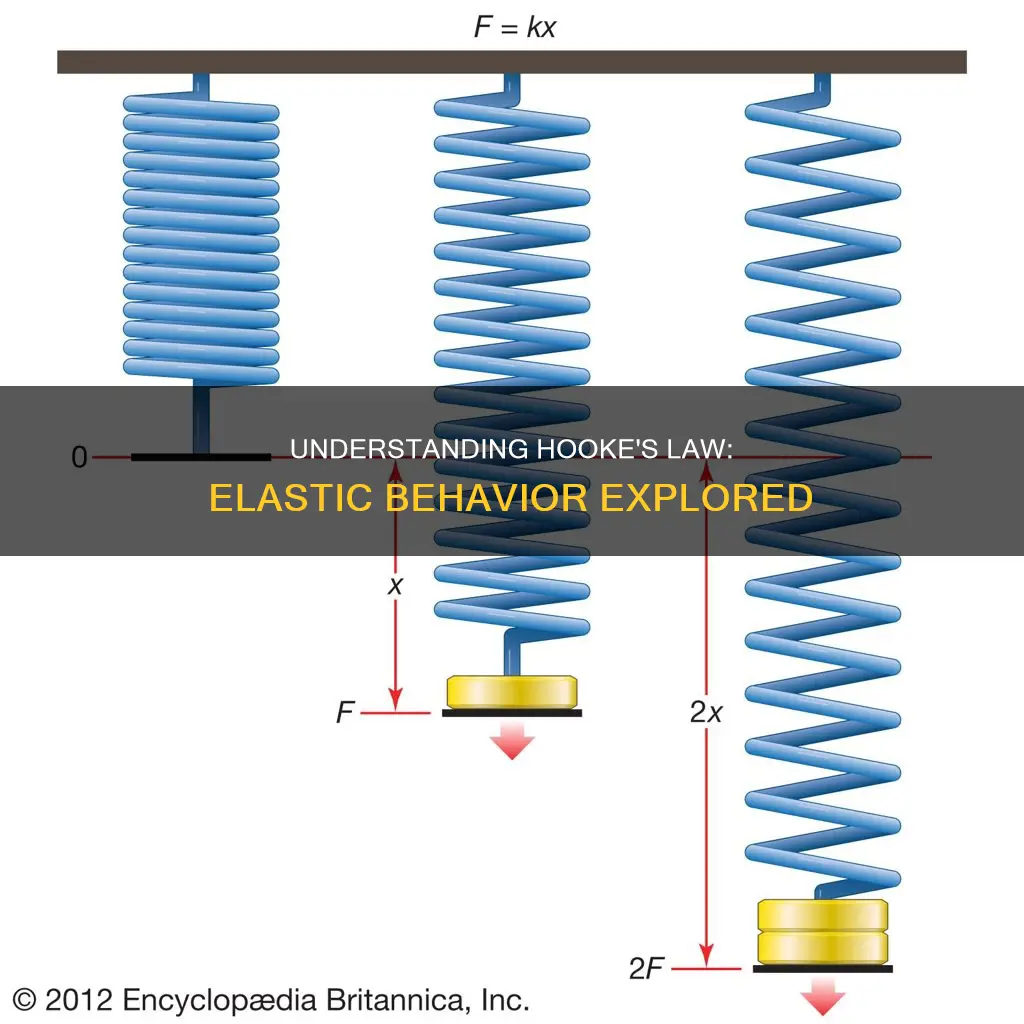
| Mathematical Expression | F = kx, where F is the force, k is the spring constant, and x is the displacement |
| Elasticity | Applicable to elastic bodies or materials, also known as linear-elastic or Hookean |
| Accuracy | Accurate for most solid bodies if the forces and deformations are small |
| Limitations | Does not apply beyond the elastic limit of a material; ceases to be accurate when forces exceed a certain limit |
What You'll Learn

Hooke's Law is a principle of physics
Hooke's Law states that the force required to extend or compress a spring is directly proportional to the distance of that extension or compression. In other words, the more you stretch or compress a spring, the greater the force needed to do so. This is known as a linear relationship, and it can be observed in many elastic materials, such as springs and rubber bands.
The law can be expressed mathematically as F = -kx, where F is the force applied to the spring, X is the displacement of the spring, and k is the spring constant, which indicates how stiff the spring is.
Hooke's Law is a foundational principle in several fields, including seismology, acoustics, and molecular mechanics. It also has practical applications in everyday objects such as clocks, scales, and suspension systems.
Understanding HIPAA Laws: Do They Cover Workers' Compensation?
You may want to see also

It applies to any elastic object
Hooke's Law, or the law of elasticity, applies to any elastic object, regardless of its complexity. This includes objects such as springs, rubber bands, and even the human lungs.
The law states that the force required to extend or compress an elastic object is directly proportional to the distance it is stretched or compressed. In other words, the more you stretch or compress an elastic object, the greater the force needed to do so.
Hooke's Law can be expressed mathematically as F = kx, where F is the force applied, x is the displacement or change in length, and k is a constant that depends on the type of elastic material, its dimensions, and its shape.
This law is named after 17th-century British physicist Robert Hooke, who discovered it in 1660 and published his findings in 1678. Hooke's Law is a fundamental principle in physics and has many practical applications, such as in the creation of the mechanical clock, spring scale, and manometer.
Alienation of Affection: NYC's Stance on Emotional Infidelity
You may want to see also

It was discovered by Robert Hooke
Hooke's Law, or the law of elasticity, was discovered by English scientist Robert Hooke in 1660. Hooke was studying springs and elasticity when he noticed that many materials exhibited similar properties when the stress-strain relationship was studied. He found that there was a linear region where the force required to stretch the material was proportional to the extension of the material.
Hooke's Law states that the strain of a material is proportional to the applied stress within the elastic limit of that material. When elastic materials are stretched, their atoms and molecules deform until stress is applied, and when the stress is removed, they return to their initial state.
The law can be expressed mathematically as F = -kX, where F is the force applied to the spring, X is the displacement of the spring, and k is the spring constant.
Hooke first stated the law in 1660 as a Latin anagram and then published the solution in 1678 as "ut tensio, sic vis", which translates to "as the extension, so the force" or "the extension is proportional to the force".
Hooke's Law has many practical applications, such as the creation of a balance wheel, which made possible the mechanical clock, the portable timepiece, the spring scale, and the manometer (or pressure gauge). It also laid the basis for studies of stress and strain and for understanding elastic materials.
Squatter Laws: Do They Apply to Children?
You may want to see also

It states that stress is directly proportional to strain
Hooke's Law, also known as the law of elasticity, was discovered by English scientist Robert Hooke in the 17th century. Hooke's Law states that, for relatively small deformations of an object, the displacement or size of the deformation is directly proportional to the deforming force or load. In other words, the stress is directly proportional to the strain.
Stress and strain take different forms depending on the situation. Generally, for small deformations, the stress and strain are proportional to each other. This is known as Hooke's Law.
Hooke's Law can be expressed mathematically as:
F = kx
Where:
- F is the applied force
- K is a constant
- X is the displacement or change in length
The value of k depends on the type of elastic material, as well as its dimensions and shape.
Hooke's Law is a fundamental principle in physics with various applications, including the creation of a balance wheel, which made mechanical clocks, portable timepieces, spring scales and manometers possible. It is also the basis for seismology, acoustics and molecular mechanics.
However, it is important to note that Hooke's Law has limitations. It only applies to elastic materials and small deformations. If the deformation is too large, the material may undergo permanent deformation or a change of state.
Florida's Ultrasound Law: Impact on Miscarriage Treatment
You may want to see also

It is the foundation of seismology, acoustics and molecular mechanics
Hooke's law is foundational to seismology, acoustics, and molecular mechanics.
Seismology
Hooke's law is foundational to seismology, the scientific study of earthquakes and the propagation of elastic waves through the Earth. Seismology is concerned with understanding earthquakes and the way in which elastic waves move through different types of Earth materials. Hooke's law is relevant to this field because it describes the behaviour of elastic materials when they are compressed or extended.
Acoustics
Hooke's law is foundational to acoustics, the branch of physics that studies mechanical waves in solids, liquids, and gases, including topics such as vibration, sound, ultrasound, and infrasound. Hooke's law is relevant to this field because it describes the behaviour of elastic materials when they are compressed or extended, which is related to the production and transmission of sound waves.
Molecular Mechanics
Hooke's law is foundational to molecular mechanics, a branch of chemistry and physics that uses classical mechanics to model molecular systems. Hooke's law is relevant to this field because it describes the behaviour of springs, which can be used to model molecular systems.
Copyright Law: Non-Profits and Legal Protection
You may want to see also
Frequently asked questions
Hooke's Law is a principle of physics that states that the force required to extend or compress a spring is proportional to the distance of that extension or compression.
The equation for Hooke's Law is F = -kx, where F is the force applied to the spring, X is the displacement of the spring, and k is the spring constant.
The spring constant, also known as the rate, is a measure of the stiffness of the spring. It is a constant factor characteristic of the spring and is measured in SI units as N/m or kg/s2.
Materials that follow Hooke's Law are known as linear-elastic or Hookean materials. This includes springs and muscular layers of the heart.
Hooke's Law only applies within the elastic limit of a material. It does not account for plastic deformation or changes of state, and many materials will deviate from the law before reaching their elastic limits.