Ohm's Law In Rlc Circuits: Understanding The Application

Ohm's law states that the voltage across a resistor is equal to the product of the resistance and the current. In other words, it describes the relationship between voltage, current, and resistance in a circuit. But does this law apply to an RLC circuit, which consists of a resistor, an inductor, and a capacitor?

In an RLC circuit, the individual resistances of the components do not simply add up. This is because inductors and capacitors behave in opposite ways, and their effects can cancel each other out. As a result, the overall behaviour of an RLC circuit is more complex, and it exhibits unique characteristics such as resonance, which has applications in radio tuners.

While Ohm's law in its basic form does not directly apply to RLC circuits, it can be adapted to analyse these circuits by taking into account the frequency-dependent behaviour of the components. This is done by introducing the concept of impedance, which is the AC analogue of resistance in a DC circuit. Impedance takes into account the effects of both inductive and capacitive reactance, in addition to resistance, and it is defined as the vector sum of these three components. By using impedance, we can apply an AC version of Ohm's law to calculate the current, voltage, and impedance in an RLC circuit.

In summary, while Ohm's law in its original form is not directly applicable to RLC circuits, it can be extended and adapted to analyse these circuits by considering the frequency-dependent behaviour of the components and introducing the concept of impedance.

Ohm's Law and complex impedances in a series RLC circuit

Ohm's law applies to RLC circuits, but only to the resistive element. In a series RLC circuit, the voltage across the resistor is in phase with the current.

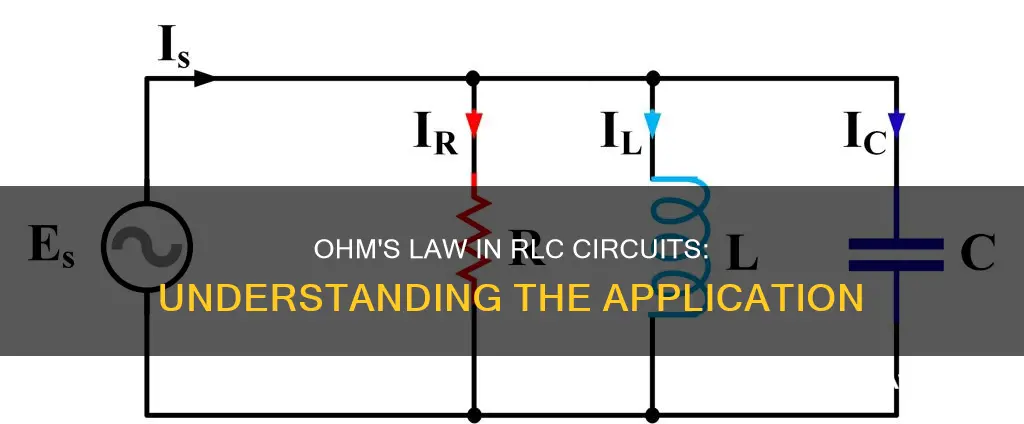
An RLC circuit consists of a resistor, an inductor, and a capacitor. The total impedance of an RLC circuit is determined by the impedance of each component. The impedance of an RLC series AC circuit is given by:

Z = sqrt(R^2 + (XL - XC)^2)

Where Z is the impedance of the circuit, R is the resistance, XL is the inductive reactance, and XC is the capacitive reactance.

In a series RLC circuit, the current is the same in each element. Using Ohm's Law, we can write the characteristic differential equation for this circuit and solve it in the frequency domain. The formula for the impedance of this circuit is:

Z = sqrt(R^2 + (X_L - X_C)^2)

Where Z is the impedance, R is the resistance, and X_L and X_C are the inductive and capacitive reactances, respectively.

The impedance of an RLC circuit can also be visualised using a vector diagram that describes the relationship between the impedances of the three components. The vector diagram will have the current vector as the reference, with the three voltage vectors plotted relative to this reference.

The analysis of a series RLC circuit is similar to that of series RL and RC circuits, except that we need to take into account the magnitudes of both XL and XC to find the overall circuit reactance. Series RLC circuits are considered second-order circuits because they contain two energy storage elements, an inductance (L) and a capacitance (C).

The phase difference between the voltage and current in an RLC circuit depends on the reactive value of the components being used. In a pure ohmic resistor, the voltage and current are in phase. In a pure inductor, the voltage leads the current by 90 degrees, and in a pure capacitor, the voltage lags the current by 90 degrees.

The impedance of an RLC circuit can also be determined using Kirchhoff's voltage law (KVL) and Kirchhoff's current law (KCL).

The phase difference between voltage and current in an RLC circuit

In a series RLC circuit, the instantaneous current flowing through the loop is the same for each circuit element. However, the voltage waveforms across each component have different phase relationships with the current.

In a pure ohmic resistor, the voltage waveform is "in-phase" with the current. In a pure inductance, the voltage waveform "leads" the current by 90 degrees, and in a pure capacitance, the voltage waveform "lags" the current by 90 degrees.

Since the inductive and capacitive reactance's XL and XC are a function of the supply frequency, the sinusoidal response of a series RLC circuit will vary with the frequency. The individual voltage drops across each circuit element of R, L, and C will be "out-of-phase" with each other.

The instantaneous voltage across a pure resistor, VR, is "in-phase" with the current. The instantaneous voltage across a pure inductor, VL, "leads" the current, while the instantaneous voltage across a pure capacitor, VC, "lags" the current. Therefore, VL and VC are 180 degrees "out-of-phase" and in opposition to each other.

The phase difference, Φ, depends on the reactive value of the components used. Reactance, (X), is zero if the circuit element is resistive, positive if it is inductive, and negative if it is capacitive.

The analysis of a series RLC circuit is similar to that of series RL and RC circuits, but the magnitudes of both XL and XC must be considered to find the overall circuit reactance.

The phase angle, θ, between the source voltage, VS, and the current, i, is the same as the angle between Z and R in the impedance triangle. This phase angle may be positive or negative, depending on whether the source voltage leads or lags the circuit current.

In summary, the phase difference between voltage and current in an RLC circuit depends on the types of components involved and their reactive values. The voltage and current can be "in-phase", or the voltage can "lead" or "lag" the current by a certain angle, typically 90 degrees in the case of pure inductance or capacitance.

Using Kirchhoff's law to calculate voltage in an RLC circuit

Kirchhoff's laws are essential tools for circuit analysis, and they can be used to calculate the voltage in an RLC circuit. There are two main Kirchhoff laws: Kirchhoff's Current Law (KCL) and Kirchhoff's Voltage Law (KVL).

Kirchhoff's Current Law (KCL)

KCL states that the total current entering a junction or node is equal to the charge leaving the node, meaning no charge is lost. In other words, the sum of currents entering and exiting a node is zero. This is also known as the conservation of charge.

Kirchhoff's Voltage Law (KVL)

KVL states that the sum of the voltages around a closed loop is equal to zero. In other words, the algebraic sum of every voltage in the loop is zero, which is known as the conservation of energy.

Using Kirchhoff's Laws to Calculate Voltage in an RLC Circuit

An RLC circuit consists of a resistor, an inductor, and a capacitor. When connected in series across an alternating supply, the RLC circuit's analysis is similar to that of series RL and RC circuits. However, the magnitudes of both inductive and capacitive reactance must be considered to find the overall circuit reactance.

In an RLC circuit, the instantaneous current flowing through the loop is the same for each circuit element. The individual voltage drops across each circuit element (resistor, inductor, and capacitor) will be "out-of-phase" with each other due to their different phase relationships with the sinusoidal alternating voltage.

The instantaneous voltage across:

• A pure resistor is "in-phase" with the current.
• A pure inductor "leads" the current by 90 degrees.
• A pure capacitor "lags" the current by 90 degrees.

Therefore, the voltages across the inductor and capacitor are 180 degrees out-of-phase and in opposition to each other.

To calculate the total voltage (V_S) across all three components in the RLC circuit, we cannot simply add the individual voltages (V_R, V_L, and V_C) because they have different directions relative to the current. Instead, we use KVL, which states that the sum of the voltages around the closed loop is equal to the sum of the EMFs.

Applying KVL to the RLC circuit, we get:

V_S = V_R + V_L + V_C

Where:

• V_S is the amplitude of the source voltage.
• V_R is the voltage drop across the resistor.
• V_L is the voltage drop across the inductor.
• V_C is the voltage drop across the capacitor.

By substituting the values of V_R, V_L, and V_C into the above equation, we can calculate the total voltage across the RLC circuit.

Additionally, we can use phasor diagrams and vector diagrams to visually represent the voltages and currents in the RLC circuit and calculate V_S vectorially.

The relationship between RLC circuits and spring-mass systems

RLC circuits are electrical circuits consisting of a resistor, an inductor, and a capacitor. They are basic building blocks of more complex analog systems and are used as fundamental models for more complex portions of electrical systems.

The RLC circuit is comparable to a mass-spring-damper system, a mechanical system consisting of a weight suspended on a spring that oscillates up and down when released. The mechanical property answering to the resistor in the circuit is friction in the spring-weight system. Friction will slowly bring any oscillation to a halt if there is no external force driving it. Likewise, the resistance in an RLC circuit will "damp" the oscillation, diminishing it over time if there is no driving AC power source in the circuit.

The RLC circuit is also comparable to a chemical engineering system. In this case, mass/inductance resists changes in direction, spring/resistance differs in force according to position, and damper/capacitor resists movement according to velocity.

How to calculate the steady state current in an RLC circuit

An RLC circuit is made up of a resistor, an inductor, and a capacitor. The impedance of an RLC circuit is determined by the impedance of each component.

In a series RLC circuit, the current is the same in each element, and the voltage drop across each component is "out-of-phase" with each other. The instantaneous voltage across a pure resistor is "in-phase" with the current, while the instantaneous voltage across a pure inductor "leads" the current by 90 degrees, and the instantaneous voltage across a pure capacitor "lags" the current by 90 degrees.

The total impedance of the series RLC circuit is given by:

Z = sqrt(R^2 + (XL - XC)^2)

Where:

• Z is the impedance of the circuit in ohms
• R is the resistance in ohms
• XL is the inductive reactance in ohms
• XC is the capacitive reactance in ohms

The steady-state current in an RLC circuit can be calculated using Ohm's law:

I = V/Z

Where:

• I is the steady-state current in amperes
• V is the voltage across the circuit in volts
• Z is the impedance of the circuit in ohms

It's important to note that in an RLC circuit, the voltage and current may be "out-of-phase," and using complex numbers or phasor diagrams can help in analyzing these circuits.

Frequently asked questions