Ohm's Law And Capacitors: What's The Relationship?

Ohm's law states that voltage is equal to the current multiplied by resistance. However, capacitors are more complex, as they store energy and resist changes in voltage rather than dissipating energy as heat. When direct current (DC) is applied to a capacitor, it offers infinite resistance and obeys Ohm's law. However, when alternating current (AC) is applied, the graph of voltage against the current does not pass through the origin, indicating non-ohmic behaviour. This is because a capacitor's resistance changes over time.

Ohm's Law and impedance

Ohms Law and Impedance

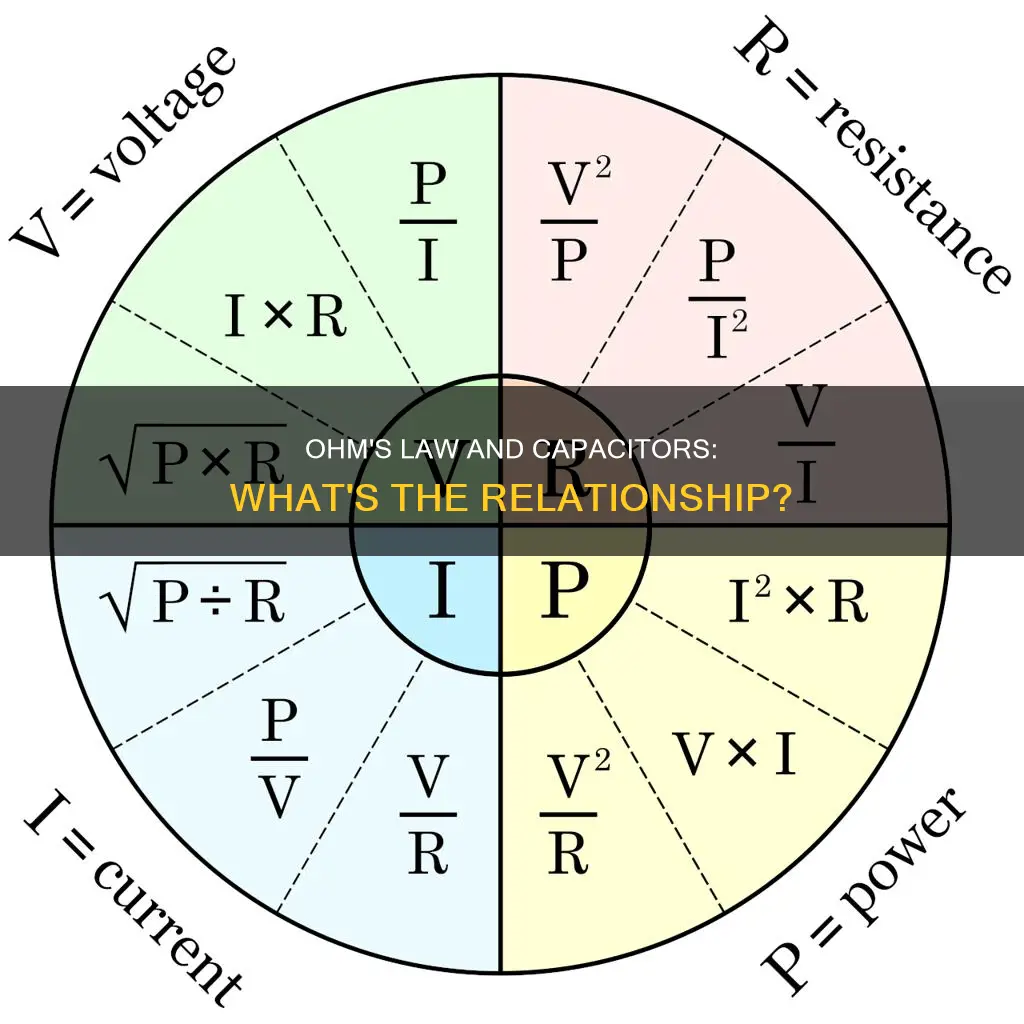
Ohm's Law, published by George Ohm in 1827, is a formula used to calculate electrical values so that we can design circuits and use electricity efficiently. It is the mathematical relationship between voltage, current, and resistance/impedance in electricity. The formula is: I = V/R, where the electrical current in a circuit can be calculated by dividing the voltage by the resistance.

When there is inductive reactance or capacitive reactance in a circuit, Ohm's Law must be adjusted to include the total impedance in the circuit. Impedance is the opposition to alternating current presented by the combined effect of resistance and reactance in a circuit. It is a complex number with the same units as resistance, the ohm, and is usually represented by the symbol Z.

The impedance of a two-terminal circuit element is the ratio of the complex representation of the sinusoidal voltage between its terminals to the complex representation of the current flowing through it. It depends on the frequency of the sinusoidal voltage. Impedance can be calculated using the following formula:

> Z = R + jX

Here, R is the resistance from resistors, and X is the reactance, which comes from the effects of capacitors or inductors. The imaginary number j is an operator that rotates a vector by 90 degrees in the counterclockwise direction.

When capacitors or inductors are used in the context of designing circuits that accept or reject specific ranges of frequencies for various applications, these circuits are called filters.

Capacitors resist changes in voltage

When the voltage across a capacitor is increased or decreased, the capacitor "resists" the change by drawing current from or supplying current to the source of the voltage change, in opposition to the change. This is different from a resistor, which dissipates energy as heat.

The voltage across a capacitor is the result of charge carriers (electrons) building up along the capacitor's dielectric. The build-up of charge carriers takes time, and therefore the change in voltage will also take time.

The time it takes for the voltage of a capacitor to change depends on the size of the capacitor. A larger capacitor will take longer to discharge or charge than a smaller one.

Capacitors are useful in electronic timing circuits because of their capacity to regulate and anticipate the rate at which they charge and discharge.

Capacitors store electric charges

Yes, capacitors store electric charges. They are devices that store electrical energy by accumulating electric charges on two closely spaced surfaces that are insulated from each other. These surfaces are often metallic plates or conductors separated by a dielectric medium, which acts to increase the capacitor's charge capacity.

The capacitor was originally known as the condenser, and the earliest forms were created in the 1740s when European experimenters discovered that electric charge could be stored in water-filled glass jars.

The charge(q), voltage (v), and capacitance(C) of a capacitor are related as follows:

Q(t) = Cv(t)

Where q(t) and v(t) are the values for charge and voltage, expressed as a function of time.

The unit of measurement for the capacitance of a capacitor is the farad, which is equal to 1 coulomb per volt. The energy stored in a capacitor (in joules) is given by the equation:

W_C(t) = 1/2Cv^2

Capacitors are widely used as parts of electrical circuits in many common electrical devices. They are used in electronic circuits for blocking direct current while allowing alternating current to pass. In electric power transmission systems, they stabilize voltage and power flow.

Capacitors are different from resistors and inductors in that the impedance is inversely proportional to the defining characteristic, i.e., capacitance.

Capacitors and inductors: the AC case

Capacitors and inductors are two common electronic components that naturally store energy. They are widely used in power networks, voltage-regulator circuits, and frequency-dependent circuits called filters.

Capacitors

Capacitance exists wherever conductive material is separated by insulating material. A capacitor is a device that stores electric charge. The current through a capacitor can be changed instantly, but it takes time to change the voltage across a capacitor.

The charge, voltage, and capacitance of a capacitor are related as follows:

Q(t) = Cv(t)

Where q(t) and v(t) are the values for charge and voltage, expressed as a function of time.

The energy stored in a capacitor (in joules) is given by the equation:

W_C(t) = 1/2 * C * v^2

Inductors

An inductor stores energy in the form of a magnetic field, usually by means of a coil of wire. An inductor resists changes in the current flowing through it. The voltage across an inductor can be changed instantly, but an inductor will resist a change in current.

The relationship between the voltage across the inductor is linearly related by a factor L, the inductance, to the time rate of change of the current through the inductor. The unit for inductance is the henry, which is equal to a volt-second per ampere.

The relationship between the voltage and the current is as follows:

V(t) = L * di/dt

The energy stored in the inductor is given by:

W_L(t) = 1/2 * L * i^2

Effects on AC Circuits

Capacitors and inductors affect AC circuits differently. In a DC circuit, a capacitor acts like an open circuit when it is fully charged or discharged, meaning no current flows through it. In an AC circuit, a capacitor acts like a resistor that depends on the frequency of the AC source. This means that the current through it varies with the frequency. The higher the frequency, the lower the resistance, and vice versa. This is called capacitive reactance.

In a DC circuit, an inductor acts like a short circuit when the current is constant, meaning the current flows through it without any voltage drop. In an AC circuit, an inductor acts like a resistor that depends on the frequency of the AC source. This means that the voltage across it varies with the frequency. The higher the frequency, the higher the resistance, and vice versa. This is called inductive reactance.

Solving AC Circuit Problems

To solve AC circuit problems, you need to use complex numbers and phasors. Complex numbers have a real part and an imaginary part, such as 3 + 4j. Phasors are vectors that represent the magnitude and phase of an AC quantity, such as voltage or current. You can use phasors to simplify AC circuit calculations by converting them to complex numbers and applying Kirchhoff's laws and Ohm's law.

Impedance, which is the ratio of voltage to current in an AC circuit, can also be used to analyze AC circuits with capacitors and inductors. Impedance provides a direct relationship between voltage and current for resistors, capacitors, and inductors when analyzing circuits with phasor voltages or currents.

Capacitors and inductors: the DC case

Capacitors and inductors are two types of electrical components with distinct properties that influence the behaviour of direct current (DC) circuits. In this section, we will delve into the characteristics of capacitors and inductors in DC circuits and explore their effects on circuit performance.

Capacitors in DC Circuits:

Capacitors are devices that store electric charge. In a DC circuit, a fully charged or discharged capacitor acts like an open circuit, preventing the flow of current. This behaviour is due to the capacitor's ability to resist changes in voltage; the voltage across a capacitor cannot change instantaneously. When connected to a battery, the current through a capacitor is determined by the voltage difference between the battery and the capacitor, as well as the internal resistance of the battery. As the capacitor charges, the voltage difference decreases, resulting in a decrease in current.

Inductors in DC Circuits:

Inductors, on the other hand, store energy in the form of a magnetic field. They resist changes in current rather than voltage. When an inductor is connected to a battery, the voltage across it can change instantaneously, but the current cannot. Initially, the inductor behaves as an open circuit, and as the current begins to flow, the inductor starts to charge. The rate of charge is determined by the formula t = L/R, where the current reaches approximately 66% of its final value after one time constant (τ).

Impedance and Ohm's Law:

To analyse circuits with capacitors and inductors, the concept of impedance is introduced. Impedance (Z) is a complex number that relates the phasor voltage (V) and the phasor current (I) in an electrical device. It can be expressed as Z = R + jX, where R is the real part representing resistance, and jX is the imaginary part representing reactance. In the case of capacitors, the imaginary part is negative, indicating dominance by capacitors. For inductors, the imaginary part is positive. Impedance changes with frequency, allowing for the design of circuits that accept or reject specific frequency ranges.

Practical Applications:

The behaviour of capacitors and inductors in DC circuits has practical implications. For instance, Boost Converters utilise inductors to increase DC voltage. Inductors can also be used in DC-DC Boost Converters to double the input voltage. Additionally, inductors are employed in generators, where a coil of wire passing through a magnetic field induces a current, leading to the creation of large currents in power generating stations.

Frequently asked questions