The Ideal Gas Law: When Does It Fail?

The ideal gas law, also known as the general gas equation, is a mathematical relationship between the pressure, volume, temperature, and number of moles of an ideal gas. The ideal gas law is a good approximation of the behavior of many gases under many conditions, but it has several limitations and breaks down under certain circumstances. The law states that the product of the pressure and volume of a gas is equal to the number of moles of the gas multiplied by the ideal gas constant and the absolute temperature. Deviations from the ideal gas law occur at very high pressures and very low temperatures, when the gas particles start to interact with each other and the volume they occupy becomes significant compared to the container volume. Additionally, the attractive forces between molecules can become significant, affecting the behavior of the gas. The Van der Waals equation is often suggested as an alternative to account for deviations from the ideal gas law due to molecular size and intermolecular forces.

High pressures

The ideal gas law is a mathematical relationship between the pressure, volume, temperature, and number of moles of an ideal gas. It is represented by the formula:

PV = nRT

Where:

• P is pressure
• V is volume
• N is the number of moles
• R is the gas constant
• T is temperature

The ideal gas law breaks down when the gas deviates from ideal behaviour, such as at high pressures. This is because the gas particles are forced closer together and start to interact with each other, resulting in a decrease in the volume of the gas. This leads to a deviation from ideal behaviour, as the ideal gas law assumes that gas particles have no intermolecular forces and occupy negligible volume.

At high pressures, the ideal gas equation breaks down because the gas particles are forced closer together, increasing the significance of intermolecular forces. This results in a decrease in the volume of the gas, as the particles occupy a larger proportion of the total volume. The ideal gas law assumes negligible volume and no intermolecular forces, so these conditions directly contradict its underlying assumptions.

The Van der Waals equation is often suggested as an alternative to the ideal gas law at high pressures, as it accounts for deviations caused by molecular size and intermolecular forces. The Van der Waals equation includes additional constants that provide information on deviations from the ideal gas law. These constants are related to the actual pressure and temperature, with deviations from the ideal gas law represented by a compressibility factor, z.

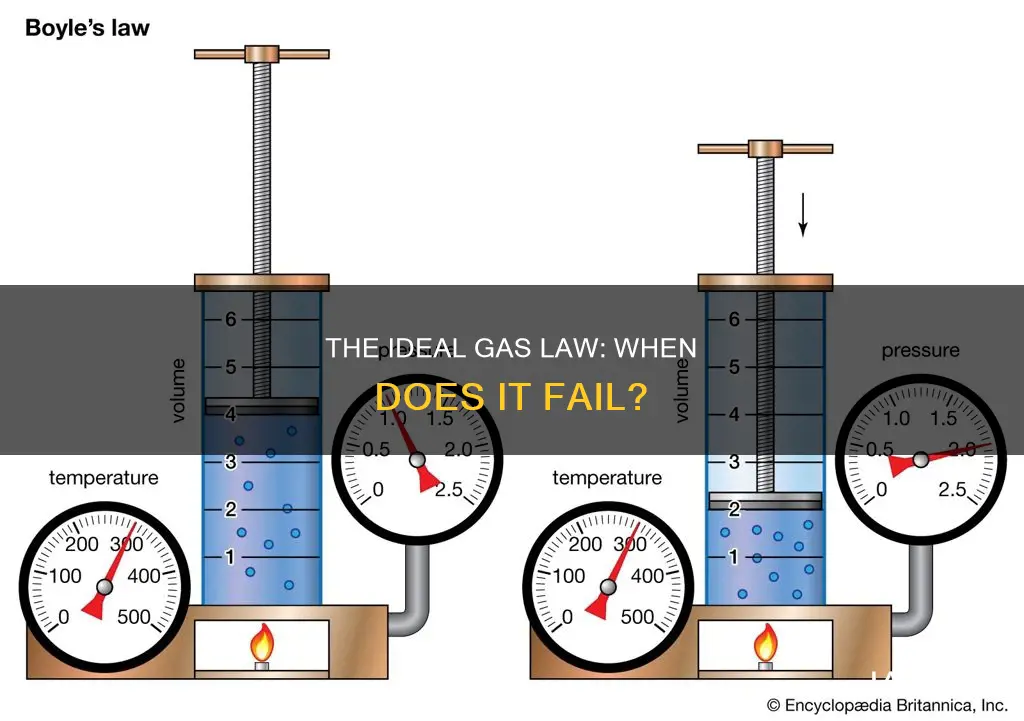
The ideal gas law is derived from combining Boyle's Law, Charles's Law, Avogadro's Law, and Gay-Lussac's Law. It is a good approximation of the behaviour of many gases under certain conditions, but it has limitations and breaks down at high pressures. The law is most accurate for monatomic gases at high temperatures and low pressures, as the neglect of molecular size and intermolecular attractions becomes less significant under these conditions.

In summary, the ideal gas law breaks down at high pressures because the assumptions of negligible volume and no intermolecular forces are violated. Gas particles are forced closer together, increasing the significance of intermolecular forces and resulting in a decrease in volume. Alternative equations, such as the Van der Waals equation, are more suitable for describing gas behaviour under these conditions.

Low temperatures

The ideal gas law fails at low temperatures because the assumptions that underpin it begin to break down. The ideal gas law assumes that gas particles have negligible volume, that they are all the same size, and that they do not have intermolecular forces. However, at low temperatures, gas particles have less kinetic energy and move slower, making it more likely that they will interact with each other. This interaction causes the gas particles to occupy a larger volume, violating the assumptions of the ideal gas law.

The ideal gas law is represented by the formula PV = nRT, where P is pressure, V is volume, n is the number of moles, R is the gas constant, and T is temperature. This equation is derived from Charles's, Boyle's, and Gay-Lussac's laws, which establish the relationships between temperature, pressure, and volume for gases.

At low temperatures, the particles of a gas slow down and do not move as quickly within the system. This decrease in kinetic energy increases the likelihood of intermolecular forces and interactions between particles. These interactions can include attractive or repulsive forces, such as hydrogen bonds or the availability of extra pairs of electrons. As a result, the volume occupied by the gas particles becomes more significant compared to the volume of the container, deviating from the ideal behaviour assumed in the gas law.

The inaccuracy of the ideal gas law at low temperatures is gradual and depends on the level of accuracy required for a given application. The law assumes that gas particles do not interact with each other except during elastic collisions, and that they do not occupy any space. However, at low temperatures, these assumptions become less valid as the particles are forced closer together and are more likely to interact.

To account for deviations from ideal gas behaviour at low temperatures, the Van der Waals equation can be used. This equation includes constants that provide information on deviations from the ideal gas law and takes into account intermolecular forces and the volume occupied by gas molecules. The compressibility factor can also be used to understand deviations from the ideal gas law, as it represents the ratio of the real volume of a gas to its ideal volume.

Intermolecular forces

The ideal gas law is a mathematical relationship between the pressure, volume, temperature, and number of moles of an ideal gas. It is represented by the formula:

$$PV = nRT$$

Where:

• $P$ is pressure
• $V$ is volume
• $n$ is the number of moles
• $R$ is the gas constant
• $T$ is temperature

The ideal gas law assumes that gases have no intermolecular forces and occupy negligible volume. This means that gas particles do not interact with each other and the volume they occupy is much smaller compared to the volume of the container they are in. However, in reality, gas particles do experience intermolecular forces, especially at high pressures and low temperatures.

At high pressures, the ideal gas equation breaks down because the gas particles are forced closer together, increasing their interactions and decreasing the volume of the gas. This results in a deviation from ideal behaviour.

Similarly, at low temperatures, gas particles have lower kinetic energy and move slower, making it more likely for them to interact with each other and occupy a larger volume. This also leads to a deviation from the ideal gas law.

The Van der Waals equation is often suggested as an alternative to account for these deviations from ideal behaviour. This equation includes constants that provide information on how much a gas deviates from ideal behaviour at different pressures and temperatures.

Molecular size

The ideal gas law breaks down when the gas deviates from ideal behaviour, such as at high pressures or low temperatures. This is because the gas particles start to interact with each other, and the volume they occupy becomes significant compared to the container volume. The ideal gas law also breaks down when the attractive forces between molecules become significant.

The ideal gas law is:

PV = nRT

Where:

• P is the absolute pressure of the gas
• V is the volume of the gas
• N is the amount of substance of gas (also known as the number of moles)
• R is the ideal, or universal, gas constant
• T is the absolute temperature of the gas

The ideal gas law is a good approximation of the behaviour of many gases under many conditions, although it has several limitations. It neglects molecular size and intermolecular attractions, so it is most accurate for monatomic gases at high temperatures and low pressures. The neglect of molecular size becomes less important at lower densities, i.e. for larger volumes at lower pressures, because the average distance between adjacent molecules becomes much larger than the molecular size.

Volume of gas particles

The ideal gas law, also known as the general gas equation, is a good approximation of the behaviour of many gases under many conditions. However, it has several limitations and breaks down at very high pressures and very low temperatures. The ideal gas law is given as:

PV = nRT

Where P is the absolute pressure of the gas, V is the volume of the gas, n is the amount of substance of gas (also known as the number of moles), and R is the ideal gas constant.

The ideal gas law assumes that gas particles do not interact with each other and that the volume they occupy is much smaller compared to the volume of the container they are in. However, at high pressures, the gas particles are forced closer together and start to interact with each other, resulting in a decrease in the volume of the gas and a deviation from ideal behaviour.

At low temperatures, the gas particles have less kinetic energy and move slower, making it more likely for them to interact with each other and occupy a larger volume, which also leads to a deviation from ideal behaviour.

The Van der Waals equation is suggested as an alternative to the ideal gas law at high pressures and low temperatures, as it accounts for deviations caused by molecular size and intermolecular forces. The ideal gas law is most accurate for monatomic gases at high temperatures and low pressures, where the neglect of molecular size and intermolecular attractions is less significant.

The volume of gas particles is an important factor in the ideal gas law. The law assumes that the volume occupied by the gas particles is negligible compared to the volume of the container. However, at high pressures, the gas particles are forced closer together, reducing the volume of the gas. This deviation from the ideal behaviour becomes more significant as the pressure increases.

Additionally, at low temperatures, the gas particles move slower and are more likely to interact with each other. This can lead to an increase in the effective volume occupied by the gas particles, as they are no longer behaving as point masses. This deviation is more pronounced at lower temperatures, as the gas particles have less kinetic energy and are more strongly influenced by intermolecular forces.

In summary, the ideal gas law begins to break down at high pressures and low temperatures due to the increased interaction between gas particles and the deviation from the assumption of negligible volume. The volume of gas particles plays a crucial role in this breakdown, as their effective volume becomes more significant compared to the container volume under these conditions.

Frequently asked questions