The law of conservation, also known as the conservation law, is a fundamental principle in physics that describes the behaviour of physical systems over time. It states that a measurable physical property of an isolated system remains constant as the system evolves, neither being created nor destroyed, but only changing from one form to another. This law applies to various physical properties, including energy, momentum, angular momentum, mass, and electric charge. In the context of physical changes, the law of conservation holds significant relevance as it provides insights into the transformations that occur during such changes. For example, in chemical reactions, the total mass of the reactants is conserved and remains equal to the mass of the products, even as their forms change. This principle is not limited to the field of physics, as it also finds applications in chemistry, biology, geology, and engineering.
| Characteristics | Values |
|---|---|
| Physical Property | A measurable quantity |
| System | An isolated physical system |
| Conservation Laws | Energy, momentum, angular momentum, mass, electric charge |
| Conservation of Energy | Total energy remains constant |
| Conservation of Mass | Total mass remains unchanged |
| Conservation of Momentum | Total momentum remains constant |
| Conservation of Angular Momentum | Total angular momentum remains constant |
| Conservation of Electric Charge | Total electric charge remains constant |
What You'll Learn

Conservation of energy
The law of conservation of energy is a fundamental principle in physics that states that the total energy within an isolated system remains constant over time. In other words, energy cannot be created or destroyed but can only be converted from one form to another. For example, chemical energy is converted to kinetic energy when a stick of dynamite explodes. If you add up all the forms of energy released in the explosion, such as kinetic energy, potential energy, heat, and sound, you will find that they are equal to the decrease in chemical energy.
This law has broad applications in various fields, including physics, chemistry, biology, geology, and engineering. It is derived from classical mechanics but remains valid in quantum mechanics and relativistic mechanics, which have superseded classical mechanics as the most fundamental laws.
The conservation of energy is closely related to the conservation of mass. In classical physics, these two laws were considered distinct. However, special relativity revealed the equivalence of mass and energy, as described by the equation E=mc^2. This implies that any object with mass can be converted into pure energy and vice versa, although this is believed to occur only under extreme physical conditions, such as those present in the early universe or around black holes.
The conservation of energy has been a foundational principle in science for about two hundred years. It has been rigorously proven and verified with a high degree of accuracy in various experiments. Any new theory, such as quantum gravity, will need to explain why energy has always appeared to be exactly conserved in terrestrial experiments.
Driving Laws: Private Property Exemptions in the UK
You may want to see also

Conservation of mass
The law of conservation of mass, also known as the principle of mass conservation, is a fundamental concept in physics and chemistry. This law states that for any system closed to all transfers of matter and energy, the mass of the system must remain constant over time. In other words, mass can neither be created nor destroyed, only transformed or rearranged.
The conservation of mass implies that the total mass of a system before and after a physical or chemical change will remain the same. For example, in a chemical reaction, the mass of the reactants (starting materials) must be equal to the mass of the products formed. This principle is widely applied in chemistry, particularly in stoichiometry, which involves calculating the amounts of reactants and products in a chemical reaction.
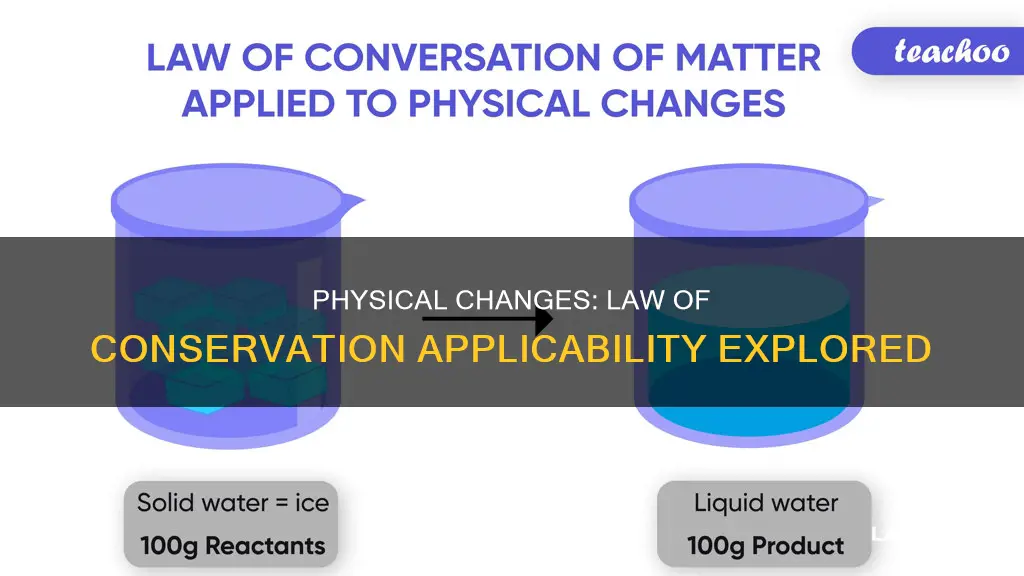
The concept of mass conservation can also be applied to physical changes, such as phase changes. For instance, when ice melts to form water, the total mass of the system remains constant even though the physical state of the substance has changed.
While the law of conservation of mass is widely accepted, it is important to note that it is not strictly accurate in certain situations. For example, in nuclear reactions and particle-antiparticle annihilation in particle physics, mass is not conserved due to the high energy involved. Additionally, mass is not generally conserved in open systems where there is an exchange of matter or energy with the surroundings.
The law of conservation of mass has played a crucial role in the development of modern science, particularly in the transition from alchemy to chemistry. It has also been generalized and unified with the law of conservation of energy, resulting in the principle of mass-energy equivalence, as described by Albert Einstein's famous equation, E=mc².
Divorce Laws: Non-Citizen Rights and Legal Protection
You may want to see also

Conservation of linear momentum
The law of conservation applies to physical changes, and one such example is the conservation of linear momentum.
Definition of Linear Momentum
Linear momentum is defined as the product of the mass of a particle and its velocity. It is a vector quantity, meaning it has both magnitude and direction. The mathematical expression for linear momentum is:
Linear Momentum = Mass x Linear Velocity
The law of conservation of linear momentum states that the total momentum of a system before an action remains equal to the total momentum of the system after the action. In other words, the momentum of a system is conserved if there is no net external force acting on it.
Mathematically, this can be expressed as:
Initial Momentum = Final Momentum
This principle applies to both linear momentum and angular momentum. It is important to note that while the total momentum of the system remains constant, the momentum of individual particles within the system may increase or decrease.
Applications of Conservation of Linear Momentum
The conservation of linear momentum has various applications in physics and engineering. One example is understanding car crashes to improve safety. It is also used in sports, such as predicting the motion of a baseball after being hit or the movement of players during a tackle.
Another application is in the launching of rockets. When a rocket's fuel burns, the exhaust gases are pushed downwards, and as a result, the rocket is propelled upwards. This is due to the conservation of momentum, where the total momentum of the system (rocket + exhaust gases) remains constant.
Elastic and Inelastic Collisions
The law of conservation of linear momentum applies to both elastic and inelastic collisions. In an elastic collision, two objects collide and then bounce apart, such as a basketball bouncing off the floor. In an inelastic collision, the objects collide and stick together, like a car crash.
Despite the difference in behaviour, the main similarity between these collisions is that momentum is conserved. However, this usually needs to account for energy lost in the form of sound or heat produced during the collision.
Requirements for Momentum Conservation
For the momentum of a system to be conserved, two requirements must be met:
- The mass of the system must remain constant during the interaction.
- The net external force on the system must be zero.
If these conditions are satisfied, the system is said to be a closed or isolated system, and the total momentum of such a system is always conserved.
Summary
The conservation of linear momentum is a fundamental principle in physics, stating that the total linear momentum of a system before and after an action remains constant. It has broad applications and is essential for understanding and predicting the behaviour of objects in motion.
Ex Post Facto Laws: Still Applicable or Archaic?
You may want to see also

Conservation of angular momentum
The law of conservation states that a measurable property of an isolated physical system does not change over time. This includes the conservation of energy, mass, linear momentum, angular momentum, and electric charge.
Angular momentum is a physical property of a spinning system, and its speed of rotation remains constant unless it is acted upon by an external torque. Angular momentum is determined by an object's mass, its velocity, and how far the mass extends out from the point of rotation. The formula for angular momentum is L = Iω, where L is angular momentum, I is rotational inertia, and ω (omega) is angular velocity.
Angular momentum is similar to linear momentum, but it also takes into account the distribution of mass around the point of rotation. It is an extensive quantity, meaning that the total angular momentum of any composite system is the sum of the angular momenta of its constituent parts.
The conservation of angular momentum means that the momentum of a rotating object does not change unless an external torque is applied. This principle can be observed in many everyday situations, such as with gyroscopes, bicycles and motorcycles, flying discs, and even figure skaters. For example, a spinning top remains upright rather than submitting to gravity and toppling over due to the conservation of angular momentum.
In the context of planets orbiting the sun, the conservation of angular momentum explains why the closer a planet is to the sun, the greater its velocity. As the distance from the sun increases, the planet's velocity decreases, but as it moves closer, its velocity increases.
Noether's theorem states that every conservation law is associated with a symmetry of the underlying physics. The symmetry associated with the conservation of angular momentum is rotational invariance, implying that the physics of a system remains unchanged if it is rotated by any angle about an axis.
Traffic Laws and Criminal Contempt: Understanding the Connection
You may want to see also

Conservation of charge
The law of conservation of charge is a fundamental principle in physics that states that the total electric charge in an isolated system remains constant over time. In other words, the net quantity of electric charge, which is the amount of positive charge minus the negative charge in a system, is always conserved. This means that the total charge of a system will never change, regardless of any internal changes or interactions within the system.
The conservation of charge is of great importance in nuclear reactions, such as alpha, beta, and gamma decay. It allows scientists to predict the final composition of a reaction accurately. According to this law, charged particles can be created or destroyed, but only if the net charge before and after these processes remains the same. This creation or annihilation of charged particles must occur in pairs of matter and antimatter with equal and opposite charges.
In particle physics, charge conservation is observed in the creation and destruction of charged particles. When charged particles are created, equal numbers of positive and negative particles are formed, thus maintaining a constant net charge. Similarly, when particles are destroyed, equal numbers of positive and negative charges are annihilated. This principle has been supported by all empirical observations to date.
The conservation of charge can be understood mathematically through a continuity equation that relates charge density and current density. This equation demonstrates that the change in electric charge within a volume of space is equal to the amount of charge flowing into that volume minus the amount flowing out. This relationship illustrates the fundamental concept of charge conservation as an accounting principle, where the amount of charge in a region is directly linked to the flow of charge into and out of that region.
The concept of charge conservation was first proposed by British scientist William Watson in 1746 and later by American statesman and scientist Benjamin Franklin in 1747. However, it was Michael Faraday who provided the first convincing proof of this principle in 1843.
Jim Crow Laws: Hispanics and Their Plight
You may want to see also
Frequently asked questions
The Law of Conservation states that a particular measurable property of an isolated physical system does not change as the system evolves over time. In other words, a certain physical property (a measurable quantity) does not change within an isolated physical system.
The Law of Conservation applies to physical changes as it does to any other change. The law implies that mass and energy can neither be created nor destroyed, only changed from one form to another. For example, in a physical change of state, the total mass of the system before and after the change remains the same.
The conservation of energy can be observed in exothermic reactions, such as burning a piece of wood, where chemical energy is released as heat. Another example is the conservation of mass in a chemical reaction, where the total mass of the reactants is equal to the total mass of the products.







