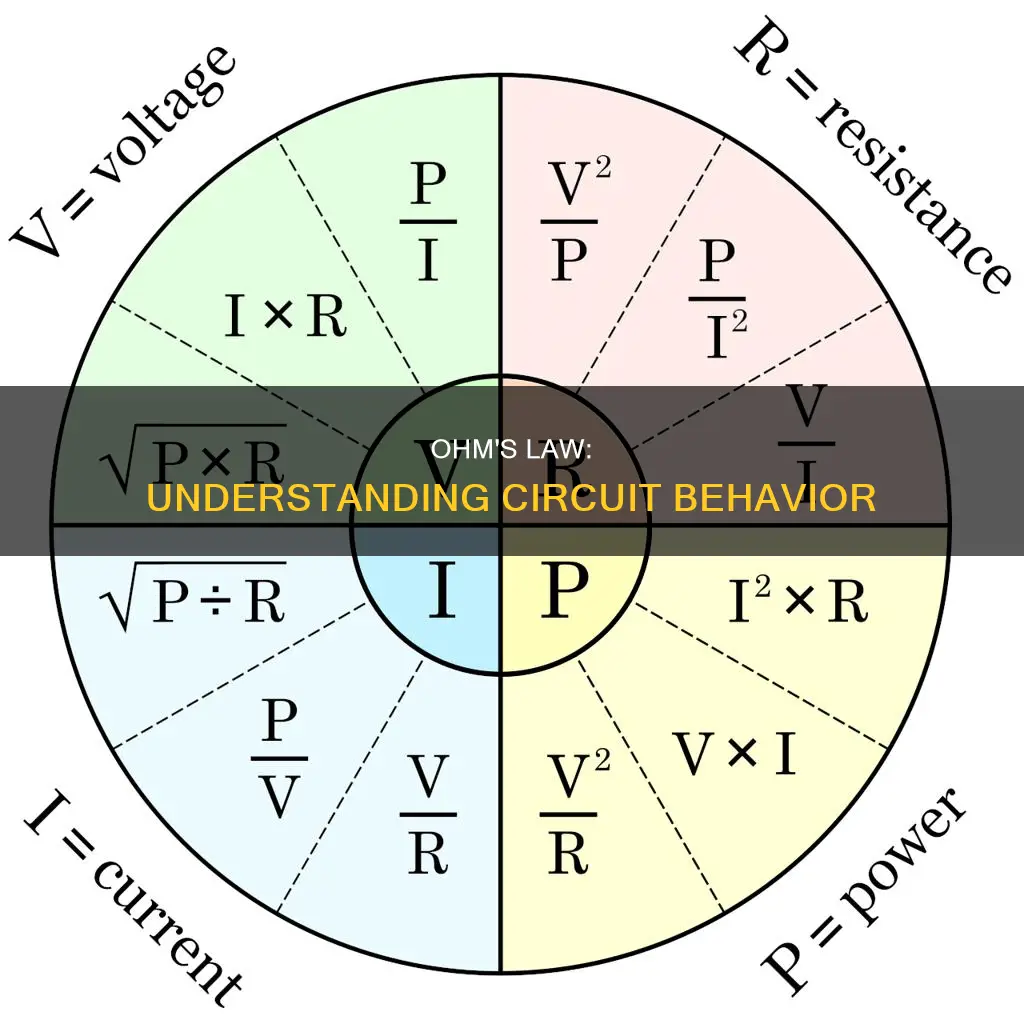
Ohm's Law is a fundamental principle in electronics, describing the relationship between voltage, current, and resistance in electrical circuits. It is a simple formula that allows for easy calculation of these three variables in any given circuit. The law was discovered by German physicist Georg Ohm and published in his 1827 paper, The Galvanic Circuit Investigated Mathematically. Ohm's Law states that the electric current through a conductor between two points is directly proportional to the voltage across those two points. By introducing the constant of proportionality, or resistance, we arrive at the equation: V = IR, where V is voltage, I is current, and R is resistance. This equation can be rearranged to solve for any of the three variables, making it a versatile tool for circuit analysis.
| Characteristics | Values |
|---|---|
| Law named after | German physicist Georg Ohm |
| Law applies to | Relationship between voltage, current and resistance in an electrical circuit |
| Mathematical equation | V = IR |
| Variables | V = voltage, I = current, R = resistance |
| Units of measurement | V = volts, I = amps, R = ohms |
| Calculating unknown values | If you know any two values, you can reconfigure the equation to calculate the third |
| Resistance calculation | Cannot be measured in an operating circuit, so Ohm's Law is useful for calculating it |
| Voltage calculation | V = IR |
| Current calculation | I = V/R |
| Resistance calculation | R = V/I |
What You'll Learn

Calculating electric power
Ohm's Law is a fundamental formula in electronics, used to calculate the relationship between voltage, current, and resistance in an electrical circuit. It was discovered by German physicist Georg Ohm and published in 1827. The law states that the amount of electric current flowing through a conductor is directly proportional to the voltage imposed on it.
Ohm's Law can be used to calculate electric power in a circuit, which is the rate at which electrical energy is transferred or dissipated. Power (P) in watts can be calculated by multiplying the voltage (V) in volts by the current (I) in amps:
P (watts) = V (volts) x I (amps)
For example, let's say we have a circuit with a battery voltage of 18 volts and a lamp resistance of 3 ohms. Using Ohm's Law (I = V/R), we can calculate the current:
I = 18 volts / 3 ohms = 6 amps
Now that we know the current, we can calculate power by multiplying the current by the voltage:
P = 6 amps x 18 volts = 108 watts
So, the lamp in this circuit is dissipating 108 watts of power, likely in the form of light and heat.
We can also rearrange the formula to calculate power if we know the current and resistance or the voltage and resistance:
P (watts) = I^2 (amps) x R (ohms)
P (watts) = V^2 (volts) / R (ohms)
Power in a circuit is only present when both voltage and current are present. If there is an open-circuit condition (voltage is present but no current flow), or a short-circuit condition (current flow but no voltage), the power dissipated in the circuit is zero.
Electrical power is typically dissipated in the form of heat (heaters), mechanical work (motors), radiated energy (lamps), or stored energy (batteries).
The First Law's Applicability to Open Systems
You may want to see also

Voltage, current and resistance
Ohm's Law is a fundamental formula in electronics that describes the relationship between voltage, current, and resistance in an electrical circuit. It was discovered by German physicist Georg Ohm and published in 1827.
Voltage, current, and resistance are key quantities in circuits. Voltage is the force that motivates charge carriers to flow in a circuit and is measured in volts. Current refers to the flow of electric charge through the conductors of a circuit and is measured in amps. Resistance is the opposition to the flow of current and is measured in ohms.
Ohm's Law is expressed by the equation:
V = IR
Where:
- V = Voltage (measured in volts)
- I = Current (measured in amps)
- R = Resistance (measured in ohms)
This equation can be rearranged to solve for any one of the variables, as long as the other two are known:
I = V/R
R = V/I
Ohm's Law is a valuable tool for technicians and engineers working with electrical circuits. It allows them to calculate unknown values of voltage, current, or resistance in a circuit. For example, if the voltage and current are known, Ohm's Law can be used to determine the resistance in the circuit. This is especially useful since resistance cannot be measured in an operating circuit.
Ohm's Law also has applications beyond circuit analysis. It can be used to validate static values of circuit components, current levels, voltage supplies, and voltage drops. For instance, if a test instrument detects abnormal current measurements, it could indicate an issue with resistance or voltage, pointing to a potential problem in the supply or circuit.
Abortion Laws: Ectopic Pregnancy Exclusion?
You may want to see also

Using Ohm's Law to calculate current in a circuit
Ohm's Law is a fundamental principle in electronics, as important to students of electrical circuits as Einstein's Relativity equation is to physicists. It defines the relationship between voltage, current, and resistance in a circuit.
Ohm's Law states that the voltage across a conductor is directly proportional to the current flowing through it, as long as physical conditions and temperature remain constant. In other words, it takes one volt of pressure to push one amp of current through one ohm of resistance.
The law is expressed by the equation: V = I x R or Voltage = Current x Resistance.
To calculate the current in a circuit using Ohm's Law, you need to know the voltage and resistance in the circuit. You can then rearrange the equation to: I = V/R or Current = Voltage/Resistance.
For example, if you have a voltage of 12V and a resistance of 6Ω, the current in the circuit will be 2A.
Ohm's Law is named after German physicist Georg Ohm, who discovered the relationship in 1827.
Lemon Law: Where You Buy or Register?
You may want to see also

Choosing a resistor for an LED
Ohm's Law is a fundamental formula in electronics that describes the relationship between voltage, current, and resistance in an electrical circuit. It was discovered by German physicist Georg Ohm and published in his 1827 paper, "The Galvanic Circuit Investigated Mathematically". The law is represented by the equation:
Voltage (V) = Current (I) x Resistance (R)
Technicians and students of electronics use this equation to calculate unknown values of voltage, current, or resistance in a circuit, given the other two values. This is especially useful for troubleshooting and understanding the behaviour of electrical circuits.
Now, let's apply this knowledge to choosing a resistor for an LED (Light Emitting Diode). LEDs typically require a current limit resistor to function properly. To choose the correct resistor, you need to know the supply voltage (battery voltage) and the LED's forward voltage and forward current, which can be found on the LED's packaging or the supplier's website.
The first step is to calculate the voltage drop across the resistor. This is done by subtracting the LED's forward voltage from the supply voltage. Next, we can use Ohm's Law to calculate the resistance. Divide the voltage drop across the resistor by the LED's forward current (in amperes) to find the resistance value in ohms.
For example, let's say we have a 9V battery powering an LED with a forward voltage of 3.2V and a forward current of 20mA. The voltage drop across the resistor is 9V - 3.2V = 5.8V. Using Ohm's Law, we can calculate the resistance as follows: Resistance = 5.8V / 0.02A = 290 ohms. So, a 290-ohm resistor, or the closest available value, would be suitable for this LED.
It's important to note that some LEDs, such as colour-changing LEDs, flashing LEDs, and 5V LEDs, are designed to run off a 5V supply and may not require a resistor. Standard and bright LEDs, on the other hand, typically require a current limit resistor. Additionally, online calculators and tools are available to assist in choosing the correct resistor for an LED, making the process more convenient.
Sodomy Laws: Do They Apply to Heterosexual Couples?
You may want to see also

How to remember Ohm's Law
Ohm's Law is a fundamental formula in electrical circuits, relating voltage, current, and resistance. It was discovered by Georg Ohm and published in 1827. The formula is:
Voltage = Current x Resistance
Or, in symbols:
V = I x R
Where:
- V = Voltage (measured in volts)
- I = Current (measured in amps)
- R = Resistance (measured in ohms)
This formula can be rearranged to solve for any one of the variables, given the other two. For example, if you know voltage and current, you can calculate resistance by rearranging the formula:
R = V/I
So, how can you remember Ohm's Law? Here are some tips:
- Use a mnemonic: A popular mnemonic is "Eagles over Indian and Rabbits", where the horizontal line divides two variables, and the vertical line multiplies them. So, if you want to know voltage (V), cover up or cross out the R and I, and you are left with V = IR.
- Use a triangle: Draw a triangle with the letters E, I, and R. If you want to know voltage (V), for example, cover up or remove R and I, and you are left with V.
- Use a power triangle: Another way is to use a power triangle and remember "Vault into an Indian Restaurant". Take the letter you want to solve for from the triangle, and the remaining letters will give you the formula.
- Use a song: Twinkle Twinkle Little Star, but sing "V is equal to IR".
- Use a rhyme: "Indian sees an eagle over the river".
Fireman's Rule: Does It Apply to Police Officers?
You may want to see also
Frequently asked questions
Ohm's Law states that the electric current through a conductor between two points is directly proportional to the voltage across those two points. In other words, it describes the relationship between voltage, current, and resistance in a circuit.
Resistance (R) can be calculated using the formula R = V/I, where V is voltage and I is current. If you know the voltage and current values in a circuit, you can simply divide the voltage by the current to find the resistance.
Ohm's Law is fundamental to circuit analysis as it allows technicians to determine unknown values of voltage, current, or resistance in a circuit. By rearranging the formula (V = IR) to isolate one of the variables, technicians can calculate the unknown value using the other two. This is especially useful for calculating resistance, which cannot be measured in an operating circuit.







