Avogadro's Law, also known as Avogadro's hypothesis or principle, was formulated by Italian scientist Amedeo Avogadro in 1811. The law states that the volume of a gas is directly proportional to the number of moles of gas when the temperature and pressure are held constant. In other words, if the amount of gas increases, so does its volume. This law is applicable to ideal gases and provides an approximate result for real gases. Gases with lighter molecules, such as helium and hydrogen, follow Avogadro's law more accurately than gases with heavier molecules.
| Characteristics | Values |
|---|---|
| Relationship | The volume of a gas is directly proportional to the number of moles of gas when the temperature and pressure are held constant |
| Volume | Directly proportional to the number of moles |
| Moles | Directly proportional to volume |
| Temperature | Held constant |
| Pressure | Held constant |
| Formula | V ∝ n, V/n = k, V1/n1 = V2/n2, V1n2 = V2n1 |
What You'll Learn
- How Avogadro's Law relates to the ideal gas equation?
- How to calculate the volume of one mole of gas at STP?
- How to calculate the number of neutrons in a given number of moles of an element?
- How to calculate the final volume of a gas when the number of moles is increased?
- How to calculate the final number of moles of gas in a container when its volume is increased?

How Avogadro's Law relates to the ideal gas equation
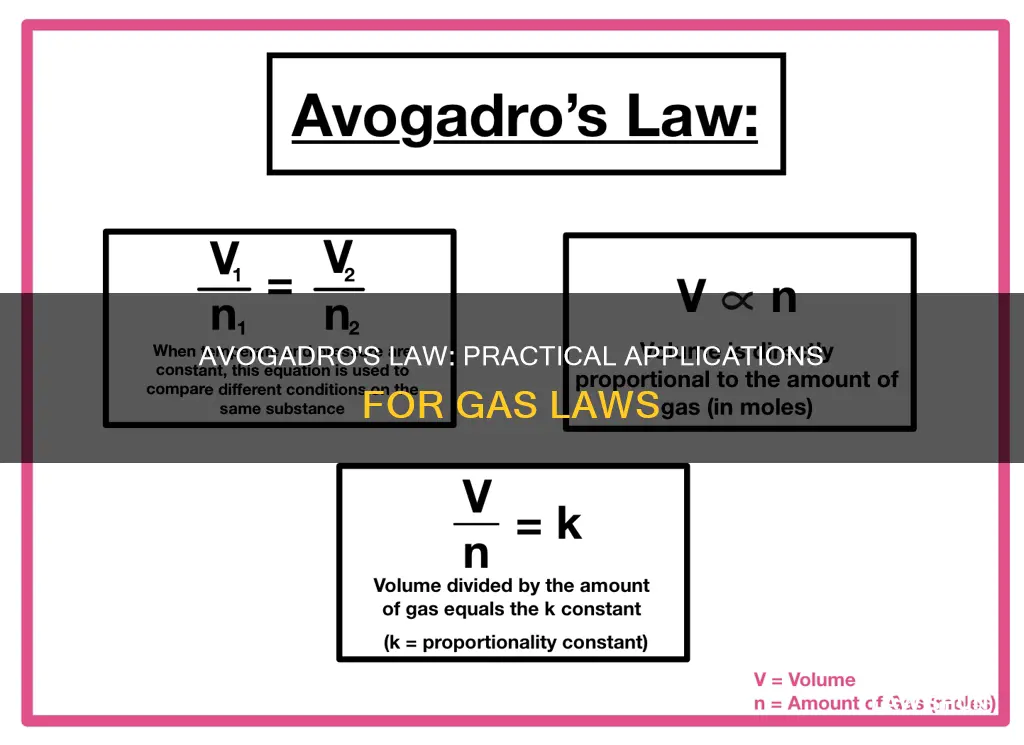
Avogadro's Law, also known as Avogadro's Principle or Hypothesis, is a gas law that relates the volume of a gas to the amount of substance of gas present. It states that the volume of a gas is directly proportional to the number of molecules of gas (measured in moles). In other words, if the amount of gas increases, so does its volume.
The law can be written as:
> V ∝ n
>
> V/n = k
Where V is the volume of the gas, n is the amount of substance of the gas (measured in moles), and k is a constant for a given temperature and pressure.
Avogadro's Law is closely related to the ideal gas equation, which combines several gas laws, including Avogadro's Law, into one formula. The ideal gas equation can be written as:
> PV = nRT
Where P is the pressure exerted by the gas, V is the volume occupied by the gas, n is the amount of substance (number of moles of gas), R is the universal gas constant, and T is the absolute temperature of the gas.
By rearranging the ideal gas equation, we can derive Avogadro's Law:
> V/n = RT/P
The value of RT/P is a constant since the temperature and pressure are kept constant. Therefore, the proportionality between the volume occupied by a gas and the number of gaseous molecules is verified.
Avogadro's Law is particularly useful for calculating the quantity of gas present in a container. It also helps determine the association between molecular mass and gas volume at standard temperature and pressure (STP). For example, at STP (101.325 kPa and 273.15 K), the volume occupied by one mole of a gas is approximately 22.4 litres.
In summary, Avogadro's Law and the ideal gas equation are closely related. Avogadro's Law describes the relationship between the volume of a gas and the amount of substance of gas present, while the ideal gas equation combines this relationship with the pressure exerted by the gas and the absolute temperature of the gas. Together, they provide valuable tools for understanding and calculating the behaviour of gases.
The Law and the Rich: Who's Exempt?
You may want to see also

How to calculate the volume of one mole of gas at STP
Avogadro's Law states that the volume of a gas is directly proportional to the number of moles (or number of particles) of gas when the temperature and pressure are held constant. In other words, Avogadro's Law tells us about the relationship between the volume of a gas and the number of molecules it possesses.
To calculate the volume of one mole of gas at STP (Standard Temperature and Pressure), we can use the Ideal Gas Law: PV = nRT, where P is the pressure, V is the volume, n is the number of moles, R is the gas constant, and T is the temperature.
First, we need to identify the values for the variables in the equation. At STP, the temperature is 0°C (273K) and the pressure is 1 atmosphere (1 atm). We are looking for the volume of one mole, so n = 1. The gas constant, R, is 0.08206 L*atm/(K*mol) or 0.08314 L*bar/(K*mol), depending on the units used.
Now, we can plug these values into the equation and solve for volume. Here is an example calculation using the first given value for R:
V = (1 mol x 0.08206 L*atm/(K*mol) x 273 K) / 1 atm
V = 22.4 L
The volume of one mole of a gas at STP is approximately 22.4 litres. This value may vary slightly depending on the specific gas and the units used, but it is generally accepted to be close to 22.4 L or 22.7 L.
Moonlighting Law: Part-Timers' Rights and Restrictions
You may want to see also

How to calculate the number of neutrons in a given number of moles of an element
Avogadro's Law states that the volume of a gas is directly proportional to the number of moles (or number of particles) of gas when the temperature and pressure are held constant. This means that as the volume of a gas increases, so does the number of moles, and vice versa.
To calculate the number of neutrons in a given number of moles of an element, you need to follow these steps:
- Identify the element and its atomic number. The atomic number represents the number of protons in the atom.
- Determine the mass number of the element. The mass number is the sum of protons and neutrons in the atom.
- Subtract the atomic number from the mass number. This will give you the number of neutrons in a single atom of the element.
- Calculate the number of moles of the element you have. You can use the formula: moles = mass/atomic mass.
- Finally, multiply the number of neutrons per atom (from step 3) by the number of moles (from step 4). This will give you the total number of neutrons in the given amount of substance.
For example, let's calculate the number of neutrons in 2 moles of magnesium (Mg). Magnesium has an atomic number of 12 and a mass number of 24. Following the steps above:
- Atomic number (protons) = 12
- Mass number (protons + neutrons) = 24
- Number of neutrons per atom = 24 - 12 = 12
- Number of moles = mass/atomic mass = 2 moles
- Total number of neutrons = number of neutrons per atom * number of moles = 12 * 2 = 24 neutrons
So, there are 24 neutrons in 2 moles of magnesium.
It's important to note that Avogadro's Law is applicable only to ideal gases and provides approximate results for real gases. Gases with lighter molecules, such as helium and hydrogen, follow Avogadro's Law more accurately compared to gases with heavier molecules.
Understanding Landlord Laws: Paperwork or Not?
You may want to see also

How to calculate the final volume of a gas when the number of moles is increased
Avogadro's Law states that the volume of a gas is directly proportional to the number of moles (or number of particles) of gas when the temperature and pressure are held constant. This means that as the number of moles of gas increases, so does the volume occupied by the gas.
The mathematical expression of Avogadro's Law is:
\[V = k \times n \nonumber \]
\[\\dfrac{V_1}{n_1} = \dfrac{V_2}{n_2} \nonumber \]
Where \(n\) is the number of moles of gas and \(k\) is a constant.
To calculate the final volume of a gas when the number of moles is increased, you can use the following steps:
- Identify the initial volume (\(V_1\)) and the initial number of moles (\(n_1\)).
- Calculate the final number of moles (\(n_2\)) by adding the additional moles to the initial number of moles.
- Rearrange the equation to solve for \(V_2\):
\[V_2 = \dfrac{V_1 \times n_2}{n_1} \nonumber \]
Substitute the known values into the equation and solve for \(V_2\).
For example, let's say you have a balloon with an initial volume of 1.90 L and it contains 0.0920 mol of helium gas. If you add 0.0210 mol of helium while keeping the temperature and pressure constant, you can calculate the new volume as follows:
\[V_2 = \dfrac{1.90 \: \text{L} \times 0.1130 \: \cancel{\text{mol}}}{0.0920 \: \cancel{\text{mol}}} = 2.33 \: \text{L} \nonumber \]
So, the final volume of the balloon is 2.33 L.
It is important to note that Avogadro's Law assumes constant temperature and pressure. If the temperature or pressure changes, the calculation may become more complex and require the use of other gas laws, such as the Ideal Gas Law.
The Laws of Motion: Saving Lives with Seat Belts
You may want to see also

How to calculate the final number of moles of gas in a container when its volume is increased
Avogadro's Law states that the volume of a gas is directly proportional to the number of moles (or number of particles) of gas when the temperature and pressure are held constant. This means that if the volume of gas in a container is increased, the number of moles will also increase.
The mathematical expression of Avogadro's Law is:
\[V = k \times n \nonumber\]
\\[\frac{V_1}{n_1} = \frac{V_2}{n_2} \nonumber\]
Where \(n\) is the number of moles of gas and \(k\) is a constant.
To calculate the final number of moles of gas in a container when its volume is increased, you can use the following steps:
- Identify the initial volume (\(V_1\)) and the initial number of moles (\(n_1\)).
- Determine the final volume (\(V_2\)).
- Use Avogadro's Law to calculate the final number of moles (\(n_2\)).
For example, let's say you have a balloon with an initial volume of \(1.90 \: \text{L}\) and it contains \(0.0920 \: \text{mol}\) of helium gas. If you add \(0.0210 \: \text{mol}\) of helium while keeping the temperature and pressure constant, you can calculate the final volume as follows:
Identify the given information:
- \(V_1 = 1.90 \: \text{L}\)
- \(n_1 = 0.0920 \: \text{mol}\)
Find the final number of moles:
\(n_2 = 0.0920 + 0.0210 = 0.1130 \: \text{mol}\)
Rearrange Avogadro's Law to solve for \(V_2\):
\(V_2 = \frac{V_1 \times n_2}{n_1}\)
Substitute the known values into the equation:
\(V_2 = \frac{1.90 \: \text{L} \times 0.1130 \: \cancel{\text{mol}}}{0.0920 \: \cancel{\text{mol}}} = 2.33 \: \text{L}\)
So, the final volume of the balloon is \(2.33 \: \text{L}\).
Remember, Avogadro's Law assumes that the temperature and pressure remain constant. If either of these variables changes, the calculation may become more complex and require the use of other gas laws, such as the Ideal Gas Law.
HIPAA Laws and Spouses: What You Need to Know
You may want to see also
Frequently asked questions
Avogadro's Law states that the volume of a gas is directly proportional to the number of moles (or particles) of gas when the temperature and pressure are held constant. In other words, if the volume of gas increases, so does the number of moles.
Avogadro's Law can be mathematically expressed as:
\[ V = k \times n \nonumber \]
\[\dfrac{V_1}{n_1} = \dfrac{V_2}{n_2} \nonumber \]
where \(n\) is the number of moles of gas and \(k\) is a constant.
Blowing up a balloon is a great example of Avogadro's Law. As you add more air or gas into the balloon, its volume increases. Conversely, when you deflate a balloon, the volume decreases as gas escapes.
Avogadro's Law assumes that gas particles have no volume and behave perfectly elastically, which is not the case with real gas molecules. However, it is still a useful approximation for real gases under normal conditions.







