Applying De Morgan's Law To Xor Gates Explained

DeMorgan's theorem is a useful tool in digital design, helping to simplify complex Boolean expressions using AND and OR gates. The theorem is taught using NAND and NOR, but it can be applied to other basic gates, including XOR. XOR, or Exclusive OR, is a logic gate that outputs 1 if one and only one input is 1. DeMorgan's theorem can be used to convert between NAND and NOR gates, and also to convert between AND and OR gates. This is done by inverting the inputs and outputs of the gate. DeMorgan's theorem can also be used to break a long bar symbol, changing the operation underneath the break from addition to multiplication, or vice versa.

De Morgan's theorem and its application to XOR

De Morgan's Theorem is a fundamental principle in Boolean algebra, which allows for the simplification of Boolean logic expressions and can be used to express logic expressions in different forms. The theorem is often taught using NAND and NOR, but it can also be applied to basic gates such as NOT, AND, OR, XOR, and XNOR.

De Morgan's Theorem states that the complement of the result obtained by OR'ing variables is equivalent to AND'ing the complements of the individual variables. In other words, when two or more input variables are AND'ed and negated, they are equivalent to the OR of the complements of the individual variables. This can be represented as A.B = A+B. Similarly, the complement of the result obtained by AND'ing variables is equivalent to OR'ing the complements of the individual variables. This means that when two or more input variables are OR'ed and negated, they are equivalent to the AND of the complements of the individual variables, represented as A+B = A.B.

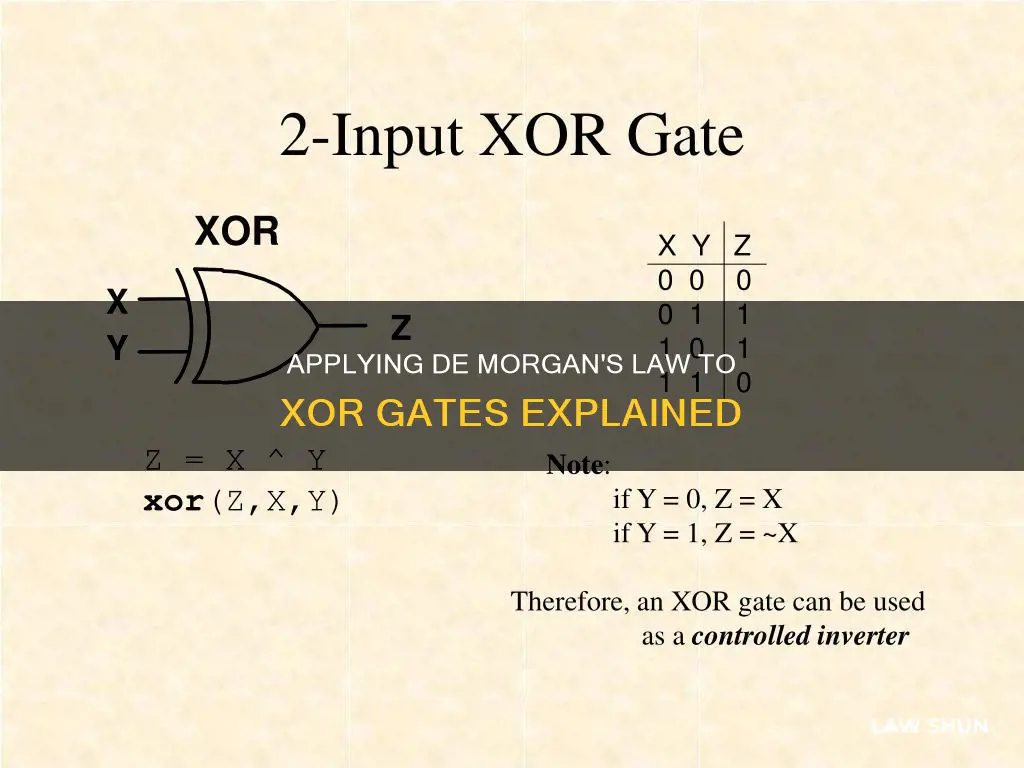
The theorem can be applied to XOR (Exclusive-OR) functions as well. XOR gates have a 1 output if one, or the other, but not both, of its inputs is zero. The output is 1 when an odd number of inputs are 1 or when the inputs are not equal. The output is 0 when the inputs are equal.

De Morgan's Theorem can be used to derive the product-of-sums form of a Boolean function from its sum-of-products form. It also helps to simplify complex Boolean expressions by "breaking" an inversion, which could be the complement of a complex Boolean expression. This makes it a powerful tool in digital design, as it allows for the simplification and alternate representation of logic circuits.

Using De Morgan's theorem to simplify XOR

De Morgan's Theorem and Laws are fundamental principles in Boolean algebra that help to simplify digital logic circuits. The theorems allow us to convert one form of a Boolean function into another, providing alternate ways to express logic functions.

De Morgan's first theorem states that when two or more input variables are AND'ed and negated, they are equivalent to the OR of the complements of the individual variables. This means that the NAND function is the same as a negative-OR function, proving that A.B = A+B.

The second theorem states that when two or more input variables are OR'ed and negated, they are equivalent to the AND of the complements of the individual variables. Thus, the NOR function is a negative-AND function, proving that A+B = A.B.

De Morgan's theorems can be applied to the XOR (Exclusive-OR) function. The XOR of two variables, x and y, can be expressed as:

X ⊕ y = xy + x y

Using De Morgan's Law, we can take the inverse of the above expression, invert the terms, and change the operator:

X ⊕ y = (xy) + (x y)

This expression can be simplified to:

~x & y

This simplification demonstrates how De Morgan's Theorem can be used to express the XOR function in an alternate form, providing a different perspective on the logic operation.

De Morgan's Theorem allows us to replace all the AND operators with OR operators, or vice versa, and then complement each term by inverting it (i.e., changing 0's to 1's and 1's to 0's) before inverting the entire function. This ability to interchange operators and invert functions is a powerful tool for simplifying complex Boolean expressions and gaining a deeper understanding of digital logic circuits.

In summary, De Morgan's Theorem provides a set of rules that enable us to transform and simplify Boolean logic expressions, particularly when applied to the XOR function. By following these rules, we can manipulate expressions to gain new insights and create equivalent logic gates with different arrangements of operators and inputs.

The difference between Exclusive OR and Inclusive OR

De Morgan's theorem and laws are essential tools for analysing and simplifying digital circuits. They allow us to convert between different logical operations, such as AND, OR, and NOT, which are represented by basic logic gates. One such operation is the XOR (Exclusive-OR) function, which is the focus of this discussion.

Now, let's delve into the difference between Exclusive OR and Inclusive OR:

Inclusive OR:

Inclusive OR is a logical operation where the output is 'true' or 'high' if any of the inputs is true. In other words, it includes the case where both inputs are true. Mathematically, this can be represented as:

A ∨ B

In a truth table, the output of an inclusive OR will be true when either A is true, or B is true, or both A and B are true. For example:

| A | B | Inclusive OR |

|---|---|---|

| 0 | 0 | 0 |

| 0 | 1 | 1 |

| 1 | 0 | 1 |

| 1 | 1 | 1 |

Inclusive OR is commonly used in digital logic and programming to represent situations where either of the conditions can be true, or both. For instance, in a programming context, if you have the statement "if x is greater than 5 or y is less than 3", the condition is satisfied if either x is greater than 5, or y is less than 3, or both conditions are true.

Exclusive OR (XOR):

Exclusive OR, on the other hand, is a logical operation where the output is true when either A is true or B is true, but not when both are true. This can be represented as:

A ⊻ B

The truth table for exclusive OR will have an output of true when either A or B is true, but the output will be false when both are true. For example:

| A | B | Exclusive OR |

|---|---|---|

| 0 | 0 | 0 |

| 0 | 1 | 1 |

| 1 | 0 | 1 |

| 1 | 1 | 0 |

Exclusive OR is useful when you want to detect differences or inequalities between two inputs. For instance, in error detection and correction in computer systems, XOR can be used to determine if there is a mismatch between two bits of data.

In summary, the key difference between Exclusive OR and Inclusive OR lies in how they treat the case where both inputs are true. Inclusive OR considers it true, while Exclusive OR considers it false. This distinction is important in digital electronics and programming, allowing for the design of complex logic circuits and algorithms.

How to apply De Morgan's theorem to multiple inputs

De Morgan's theorem is a fundamental principle in Boolean algebra that allows for the simplification of Boolean logic expressions and can be used to express logic expressions in different forms. De Morgan's theorem states that the complement of the result obtained by OR'ing variables is equivalent to AND'ing the complements of the individual variables, and the complement of the result obtained by AND'ing variables is equivalent to OR'ing the complements of the individual variables.

De Morgan's theorem can be applied to multiple inputs by using the following rules:

• De Morgan's first theorem: When two or more input variables are AND'ed and negated, they are equivalent to the OR of the complements of the individual variables. For example, the NAND function will be a negative-OR function, proving that A.B = A+B.
• De Morgan's second theorem: When two or more input variables are OR'ed and negated, they are equivalent to the AND of the complements of the individual variables. Thus, the equivalent of the NOR function is a negative-AND function, proving that A+B = A.B.

These theorems can be applied to any number of input variables, not just limited to two. For example, with three input variables A, B, and C, De Morgan's first theorem would state that (A.B.C) = (A+B+C). Similarly, with four input variables A, B, C, and D, De Morgan's second theorem would state that (A+B+C+D) = (A.B.C.D).

By applying De Morgan's theorems, we can replace all the AND (.) operators with OR (+) operators and vice versa. Additionally, we can complement each of the terms or variables in the expression by inverting it, i.e., changing 0's to 1's and 1's to 0's before inverting the entire function.

De Morgan's theorems provide a way to simplify complex Boolean expressions and are particularly powerful tools in digital design and logic gate simplification. They allow us to express logic functions in different but equivalent forms, aiding in the analysis and design of digital circuits.

The relationship between De Morgan's theorem and NAND/NOR

De Morgan's theorems are a powerful tool in digital design, especially when working with Boolean expressions and logic circuits. The theorems establish a relationship between the NAND and NOR gates, allowing for a clearer understanding of logic and facilitating simplification of complex expressions.

De Morgan's first theorem states that the NAND function, represented as A.B, is equivalent to a negative-OR function, or A+B. In other words, when two or more input variables are AND'ed and negated, they are equal to the OR of the complements of those variables. Conversely, the second theorem states that the NOR function, A+B, is equivalent to a negative-AND function, or A.B. This means that when two or more input variables are OR'ed and negated, they are equal to the AND of the complements of those variables.

These theorems can be applied to the basic logic gates, including the XOR gate. By using De Morgan's theorems, we can replace AND operators with OR operators and vice versa, and then complement each term by inverting it. This results in an alternate representation of the gate, with the same functionality but a different internal structure. For instance, an XOR gate with inverted inputs becomes equivalent to an XNOR gate, and vice versa.

De Morgan's theorems are not just theoretical concepts but have practical applications in circuit design. They allow designers to create alternate symbols for gates like NAND and NOR, emphasising the OR or AND part of the equation, respectively. This flexibility in representation helps designers match the symbols to their design intent, making the logic easier to understand and reducing potential errors.

In summary, De Morgan's theorems provide a powerful framework for working with NAND and NOR gates in digital design. By applying these theorems, designers can simplify Boolean expressions, create alternate gate symbols, and gain a deeper understanding of the relationship between different logic gates, including the XOR gate.

Frequently asked questions