Gauss's Law is a powerful tool in physics that simplifies the calculation of electric fields in situations with certain symmetries. It states that the total electric flux out of a closed surface is equal to the charge enclosed within that surface, divided by the permittivity. This law is not directly about electric fields but about electric flux, and it is particularly useful when dealing with charge distributions that exhibit spherical, cylindrical, or planar symmetry. By selecting a Gaussian surface with the same symmetry as the charge distribution, we can determine the electric field using Gauss's Law. This involves evaluating the integral over the Gaussian surface to calculate the flux and then applying the law to find the electric field. Gauss's Law is an important tool for assessing the amount of enclosed charge and has practical applications in various fields, including engineering and physics.
| Characteristics | Values |
|---|---|
| Definition | The total electric flux out of a closed surface is equal to the charge enclosed divided by the permittivity |
| Formula | Φ = → E . d → A = qnet/ε0 |
| Application | Used to calculate the electric field of charge distributions with symmetry |
What You'll Learn

Gauss Law and Electric Flux
Gauss's Law is a fundamental principle in physics that relates the electric field to the distribution of electric charges. It states that the total electric flux through any closed surface is equal to the total charge enclosed by the surface divided by the permittivity of free space (ε0). In other words, the net outward normal electric flux through any closed surface is proportional to the total electric charge enclosed within that closed surface. Gauss's Law can be expressed mathematically as:
∮S E · dA = Qenc/ε0
Where ∮S represents the surface integral over a closed surface S, E is the electric field vector, dA is the surface area vector, Qenc is the total charge enclosed by the surface, and ε0 is the permittivity of free space.
Gauss's Law is a powerful tool for calculating electric fields in situations where the symmetry of the charge distribution makes it difficult to use Coulomb's Law. By using Gauss's Law, it is possible to calculate the electric field of a uniformly charged sphere, cylinder, or plane, for example.
The concept of electric flux is closely related to Gauss's Law. Electric flux is defined as the rate of flow of the electric field through a given area. It is proportional to the number of electric field lines going through a virtual surface. Mathematically, electric flux (Φ) is given by:
Φ = ∫E⋅dA
Where E is the electric field and dA is a differential area on the closed surface S with an outward-facing surface normal defining its direction.
Gauss's Law can be applied to both uniform and non-uniform electric fields. It is a general law that applies to any closed surface and any distribution of charges. The choice of the Gaussian surface depends on the symmetry of the charge distribution. Spherical symmetry, cylindrical symmetry, and translational symmetry along a plane are the three types of symmetry to consider when choosing an appropriate Gaussian surface.
To calculate the electric flux through an arbitrary closed surface due to an arbitrary charge distribution, we can use Gauss's Law. If there are no charges inside the closed surface, the electric flux through the surface is zero. When there are charges inside the enclosed volume, Gauss's Law states that the electric flux through the surface is equal to the net charge enclosed divided by the permittivity.
Gauss's Law has important applications in many areas of physics, including electromagnetism, electrostatics, and quantum mechanics. It is used to analyze the behavior of electric fields in charged particles, capacitors, and other electrical devices. It also plays a key role in understanding electromagnetic radiation and the propagation of radio waves.
California's Privacy Law: National Reach?
You may want to see also

Gauss Law and Electric Field
Gauss's Law is a fundamental principle in physics that relates the distribution of electric charges to the resulting electric field. It is one of Maxwell's equations and is an application of the divergence theorem.
Statement of Gauss's Law
Gauss's Law states that the total electric flux through any closed surface is equal to the total charge enclosed by that surface divided by the permittivity of free space (ε0). In other words, the net electric flux through a closed surface is directly proportional to the net charge enclosed by the surface.
Mathematically, Gauss's Law can be expressed as:
> ∮S E · dA = Qenc/ε0
Where:
- ∮S represents the surface integral over a closed surface S
- E is the electric field vector
- DA is the surface area vector
- Qenc is the total charge enclosed by the surface
- Ε0 is the permittivity of free space
Gauss's Law and Electric Field
Gauss's Law can be used to calculate the electric field in situations where the symmetry of the charge distribution makes it difficult to use Coulomb's Law. It is particularly useful when there is some symmetry in the problem that mandates the electric field passes through the surface in a uniform way.
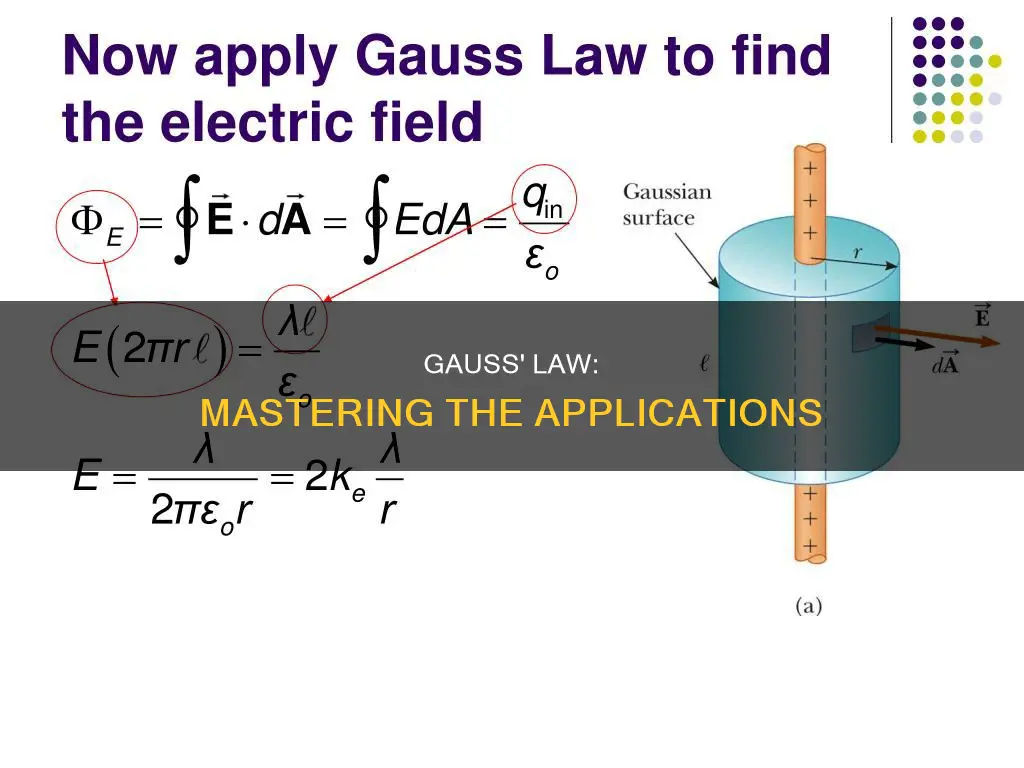
Infinite Wire: To find the electric field due to an infinite wire, assume that the charge per unit on the infinitely long wire is λ. The electric field is radially away from all points of the wire, and there is no component parallel to the line of charge. Now, assume the wire as a cylinder (with radius 'r' and length 'l') centered on the line of charge as the Gaussian surface. According to Gauss's Law:
> ϕ = E.dA = qnet ⁄ ε0
Plane Sheet of Charge: Suppose that the sheet is infinite in extent and that the charge per unit area is σ. Considerations of symmetry lead us to believe that the field direction is everywhere normal to the plane, and if there are no other charges in the world, the fields must be the same on each side. This time, we choose a rectangular box that cuts through the sheet as the Gaussian surface. According to Gauss's Law:
> ∫E⋅dA = Q/ε0
Charged Ring: For a charged ring of radius R on its axis at a distance x from the centre of the ring, the electric field becomes:
> E = 1/4πε0 * qx/((R^2+x^2)^3/2)
Plane-Charged Conductor: In a medium with a dielectric constant of K, the strength of the electric field near a plane-charged conductor is given by:
> E = σ ⁄ Kε0
Infinite Line of Charge: At a distance of ‘r’ in the case of an infinite charge line, the electric field is given by:
> E = (1 ⁄ 4 × π r ε0) (2π ⁄ r) = λ ⁄ 2π r ε0, where λ is linear charge density.
Condenser or Capacitor: The field between two parallel plates in a condenser or capacitor is given by:
> E = σ ⁄ ε0, where σ is the surface charge density.
Uconnect and Driving Laws: Texting and Legalities
You may want to see also

Gauss Law in Electrostatics
Gauss's Law is a fundamental principle in physics that relates the electric field to the distribution of electric charges. It is one of Maxwell's equations and is an application of the divergence theorem. The law was first formulated by Joseph-Louis Lagrange in 1773 and later by Carl Friedrich Gauss in 1835.
Gauss's Law states that the total electric flux through any closed surface is equal to the total charge enclosed by the surface divided by the permittivity of free space (ε0). In other words, the net electric flux through a closed surface is equal to 1/ε0 times the net electric charge enclosed within that closed surface. The closed surface is also referred to as the Gaussian surface.
The law can be expressed mathematically using vector calculus in integral and differential forms, which are equivalent since they are related by the divergence theorem (also called Gauss's theorem). The integral form of Gauss's law is:
> {\displaystyle \Phi _{E}={\frac {Q}{\varepsilon _{0}}}}
Where ΦE is the electric flux through a closed surface S enclosing any volume V, Q is the total charge enclosed within V, and ε0 is the electric constant. The electric flux ΦE is defined as a surface integral of the electric field:
> {\displaystyle \Phi _{E}=}
> {\displaystyle \scriptstyle _{S}}
> {\displaystyle \mathbf {E} \cdot \mathrm {d} \mathbf {A} }
Where E is the electric field, dA is a vector representing an infinitesimal element of the area of the surface, and · represents the dot product of two vectors.
The differential form of Gauss's law states that the divergence of the electric field is proportional to the local density of charge:
> {\displaystyle \nabla \cdot \mathbf {E} ={\frac {\rho }{\varepsilon _{0}}}}
Where ∇ · E is the divergence of the electric field, ε0 is the vacuum permittivity, and ρ is the total volume charge density (charge per unit volume).
Gauss's Law is particularly useful in situations where the symmetry of the charge distribution makes it difficult to use Coulomb's Law. It can be used to calculate the electric field of uniformly charged spheres, cylinders, or planes, for example. It also has important applications in electromagnetism, electrostatics, and quantum mechanics, and it plays a key role in understanding electromagnetic radiation and the propagation of radio waves.
Gauss's Law can also be used to derive Coulomb's Law, and vice versa. Coulomb's Law states that the electric field due to a stationary point charge is:
> {\displaystyle \mathbf {E} (\mathbf {r} )={\frac {q}{4\pi \varepsilon _{0}}}{\frac {\mathbf {e} _{r}}{r^{2}}}}
Where er is the radial unit vector, r is the radius, ε0 is the electric constant, q is the charge of the particle, and the charge is assumed to be located at the origin.
To derive Gauss's Law from Coulomb's Law, we can use the superposition principle, which states that the resulting field is the vector sum of fields generated by each particle (or the integral, if the charges are distributed smoothly in space). Using the expression from Coulomb's law and taking S in the integral form of Gauss's law to be a spherical surface of radius r centred at the point charge Q, we get:
> {\displaystyle \oint _{S}\mathbf {E} \cdot d\mathbf {A} ={\frac {Q}{\varepsilon _{0}}}}
By the assumption of spherical symmetry, the integrand is a constant, and the result is:
> {\displaystyle 4\pi r^{2}{\hat {\mathbf {r} }}\cdot \mathbf {E} (\mathbf {r} )={\frac {Q}{\varepsilon _{0}}}}
Where r̂ is a unit vector pointing radially away from the charge. Again by spherical symmetry, E points in the radial direction, and we get:
> {\displaystyle \mathbf {E} (\mathbf {r} )={\frac {Q}{4\pi \varepsilon _{0}}}{\frac {\hat {\mathbf {r} }}{r^{2}}}}
Which is essentially equivalent to Coulomb's law. Thus, the inverse-square law dependence of the electric field in Coulomb's law follows from Gauss's law.
Stark Laws: Healthcare Vendors' Compliance and Legal Boundaries
You may want to see also

Gauss Law and Coulomb's Law
Gauss's Law and Coulomb's Law are two of the most fundamental laws in physics, and they are closely related to each other.
Gauss's Law
Gauss's Law is a fundamental principle in physics that relates the electric field to the distribution of electric charges. It was formulated by Carl Friedrich Gauss in 1835 and is one of Maxwell's equations, which form the basis of classical electrodynamics.
In its simplest form, Gauss's Law states that the total electric flux through any closed surface is equal to the total charge enclosed by that surface divided by the permittivity of free space (ε0). Mathematically, this can be expressed as:
∮S E · dA = Q/ε0
Where ∮S represents the surface integral over a closed surface S, E is the electric field vector, dA is the surface area vector, Q is the total charge enclosed, and ε0 is the permittivity of free space.
Coulomb's Law
Coulomb's Law describes the force between two point electric charges. It was discovered by Charles-Augustin de Coulomb in the late 18th century and is one of the first quantitative laws encountered by students of electromagnetism.
Coulomb's Law states that the force between two static point electric charges is directly proportional to the product of their charges and inversely proportional to the square of the distance between them. Mathematically, it can be written as:
F = k * (q1 * q2) / r^2
Where F is the force between the charges, q1 and q2 are the charges, r is the distance between them, and k is the electrostatic constant.
Relationship Between Gauss's Law and Coulomb's Law
Gauss's Law and Coulomb's Law are equivalent, meaning they are one and the same thing. Either one can be derived from the other.
For example, consider a point charge q. According to Coulomb's Law, the electric field produced by it is given by:
E = kq / r^2
Where k = 1 / (4πε0). Now, if we take a sphere of radius r centred on the charge q, we can calculate the electric flux through the surface of this sphere using Gauss's Law:
∮S E · dA = ∮S kq / r^2 * ds = kq / r^2 * ∮S ds = kq / r^2 * (4πr^2) = 4πkq = q / ε0
Thus, we have derived Gauss's Law from Coulomb's Law.
Conversely, we can also start with Gauss's Law and derive Coulomb's Law. By taking the surface S in the integral form of Gauss's Law to be a spherical surface centred at a point charge Q, we get:
∮S E · dA = Q / ε0
Assuming spherical symmetry, we can take the integrand out of the integral, giving:
4πr^2 * E = Q / ε0
Since E points in the radial direction, we can rearrange to get:
E = Q / (4πr^2 * ε0)
Which is essentially equivalent to Coulomb's Law.
Therefore, the inverse-square law dependence of the electric field in Coulomb's Law follows from Gauss's Law, and vice versa.
Child Labor Laws: Family Business Exempt?
You may want to see also

Gauss Law for Magnetism
Gauss's Law for Magnetism is one of the four Maxwell's equations that underpin classical electrodynamics. It states that the divergence of the magnetic field B is equal to zero, or, in other words, that it is a solenoidal vector field. This is equivalent to stating that magnetic monopoles do not exist.
The law can be written in two forms: a differential form and an integral form. These are equivalent due to the divergence theorem.
The differential form of Gauss's Law for Magnetism is:
{\displaystyle \nabla \cdot \mathbf {B} =0}
Where ∇ · denotes divergence, and B is the magnetic field.
The integral form of Gauss's Law for Magnetism states:
{\displaystyle \Phi _{B}=
{\displaystyle \scriptstyle S}
{\displaystyle \mathbf {B} \cdot \mathrm {d} \mathbf {S} =0}
Where S is any closed surface, ΦB is the magnetic flux through S, and dS is a vector whose magnitude is the area of an infinitesimal piece of the surface S, with its direction being the outward-pointing surface normal.
Gauss's Law for Magnetism, therefore, states that the net magnetic flux through a closed surface equals zero. This means that for each volume element in space, there are the same number of "magnetic field lines" entering and exiting. No total "magnetic charge" can build up at any point in space.
This law is a physical application of Gauss's theorem (also known as the divergence theorem) in calculus. It was independently discovered by Lagrange in 1762, Gauss in 1813, Ostrogradsky in 1826, and Green in 1828.
The name "Gauss's Law for Magnetism" is not universally used, and it is also referred to as the "Absence of free magnetic poles" or the "transversality requirement".
The Executive Branch: Rule of Law in Action
You may want to see also







