Hooke's Law: When Elasticity Fails

Hooke's Law, a fundamental principle in physics, describes the linear relationship between force and displacement in a spring. However, this law is only applicable within a specific range of deformation, known as the elastic limit. When forces exceed this limit, the material's behavior deviates from Hooke's Law, and it no longer exhibits a direct proportionality between force and displacement. This phenomenon occurs due to the material's internal structure, which can be altered by excessive stress, leading to permanent deformation or even material failure. Understanding why Hooke's Law breaks is crucial for engineers and scientists to predict and control the behavior of materials under various conditions.

Material Properties: Hooke's Law holds for certain materials like metals and rubber, but not all

Hooke's Law is a fundamental principle in physics and engineering, describing the relationship between stress and strain in a material. It states that the extension of a spring is directly proportional to the force applied to it, provided the force does not exceed the material's elastic limit. This law is a cornerstone for understanding the behavior of elastic materials, particularly those like metals and rubber, which exhibit linear elasticity.

Metals, such as steel and aluminum, are excellent examples of materials that adhere to Hooke's Law. When subjected to a controlled load, these materials will deform elastically, returning to their original shape once the load is removed. This property is crucial in various applications, from the construction of bridges and buildings to the design of automotive parts and machinery. For instance, the suspension systems of vehicles rely on the elastic properties of rubber and metal springs to provide a smooth ride by absorbing shocks and vibrations.

Rubber is another material where Hooke's Law is applicable. Natural and synthetic rubbers possess a unique ability to stretch significantly under stress, demonstrating elastic behavior. This characteristic is essential in the production of tires, where the material's elasticity ensures a comfortable ride and optimal traction. Additionally, rubber's resilience is utilized in various industrial applications, such as vibration damping and sealing, where its ability to deform and return to its original shape is invaluable.

However, it is important to note that Hooke's Law does not apply to all materials. The law's validity is limited to materials that exhibit linear elasticity, meaning their deformation is directly proportional to the applied force. Materials like plastics, concrete, and certain types of wood do not follow Hooke's Law. These materials can undergo permanent deformation or even fracture when subjected to stress, making them unsuitable for applications that require elastic behavior.

The behavior of materials under stress is complex and varies widely depending on the material's properties and the conditions of deformation. Some materials may exhibit non-linear responses, where the stress-strain relationship is not directly proportional. In such cases, more advanced models and equations, such as the von Mises yield criterion or the Ramberg-Osgood equation, are used to describe the material's behavior. Understanding these nuances is crucial for engineers and scientists to select the appropriate materials for specific applications and ensure the safe and efficient design of structures and systems.

Stress-Strain Curves: The linear region in these curves is where Hooke's Law applies

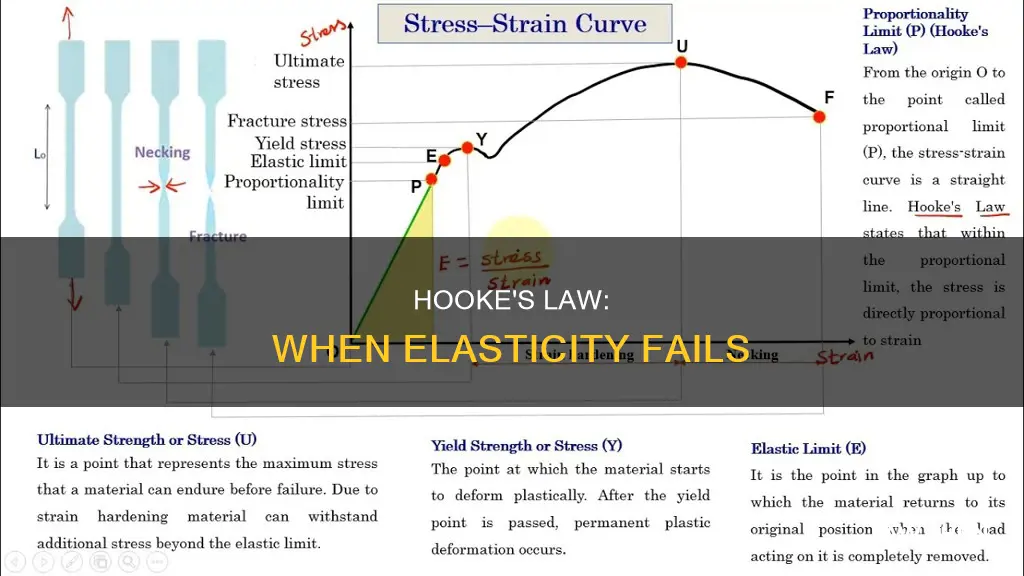
Hooke's Law is a fundamental principle in physics and engineering, stating that the extension of a spring is directly proportional to the force applied to it, within certain limits. This law is often represented graphically through stress-strain curves, which illustrate the relationship between the stress (force per unit area) and strain (deformation) of a material. The linear region on these curves is where Hooke's Law holds true, providing a clear and useful relationship between stress and strain.

Stress-strain curves typically show a straight line when the material behaves elastically, meaning it returns to its original shape after deformation. In this linear region, the stress and strain are directly proportional, and the slope of the line represents the material's elastic modulus, a measure of its stiffness. This is the point where Hooke's Law is most applicable, and it is a critical concept for understanding material behavior.

However, as the force or stress applied to the material increases, it will eventually exceed the elastic limit, and the curve will deviate from a straight line. This is the point where Hooke's Law breaks down. The material may undergo plastic deformation, where it permanently deforms without returning to its original shape, or it may even fracture. The non-linear region of the stress-strain curve indicates that the material is no longer following Hooke's Law and is instead exhibiting more complex behavior.

The transition from the linear region to the non-linear region is a critical point of interest in material science and engineering. It is where the material's properties change, and it can be influenced by various factors such as temperature, material composition, and the presence of impurities. Understanding this transition is crucial for designing materials that can withstand specific conditions and forces.

In summary, the linear region on stress-strain curves is where Hooke's Law applies, providing a simple and useful relationship between stress and strain. Beyond this region, the material's behavior becomes more complex, and Hooke's Law no longer holds. This understanding is essential for engineers and scientists to predict and control the performance of materials under various conditions.

Elastic Limit: Beyond this limit, Hooke's Law no longer holds true

The concept of Hooke's Law is fundamental in understanding the behavior of elastic materials, but it is essential to recognize that this law has its limitations. Hooke's Law states that the extension of a spring is directly proportional to the force applied to it, provided the deformation is within the elastic limit. However, when the force exceeds this limit, the law no longer holds, and the material's behavior changes.

The elastic limit is the point at which a material's deformation becomes permanent, and it is unique to each material. Beyond this limit, the material can no longer return to its original shape when the force is removed. This phenomenon is often referred to as the material's yield point. When a force is applied to a material beyond its elastic limit, it undergoes plastic deformation, where the atoms or molecules within the material rearrange, leading to a permanent change in shape.

In the context of Hooke's Law, the elastic limit is crucial because it defines the range of forces over which the law is applicable. If a force is applied within this limit, the material will deform elastically, and the relationship between force and extension will be linear, as described by Hooke's Law. However, once the force exceeds the elastic limit, the material's response becomes non-linear, and the law no longer accurately predicts the material's behavior.

Materials scientists and engineers must consider the elastic limit when designing structures or systems that rely on elastic materials. Exceeding this limit can lead to unexpected behavior, reduced material strength, and even structural failure. For example, in the field of mechanics, understanding the elastic limit is vital for designing springs, which are commonly used in various applications. If a spring is subjected to forces beyond its elastic limit, it may not return to its original shape, leading to potential performance issues.

In summary, Hooke's Law is a valuable tool for understanding the relationship between force and deformation in elastic materials, but it is essential to recognize the existence of the elastic limit. Beyond this limit, the material's behavior deviates from Hooke's Law, and plastic deformation occurs. Awareness of this limit is crucial for engineers and scientists to ensure the safe and efficient use of elastic materials in various applications.

Non-Linear Behavior: Some materials exhibit non-linear stress-strain relationships, breaking Hooke's Law

The concept of Hooke's Law, which states that the extension of a spring is directly proportional to the force applied to it, is a fundamental principle in physics. However, in the real world, many materials do not follow this linear relationship, leading to a phenomenon known as non-linear behavior. This deviation from Hooke's Law occurs when the stress-strain curve of a material does not follow a straight line, indicating that the material's response to deformation is not directly proportional to the applied force.

Non-linear behavior is observed in various materials, including metals, polymers, and even biological tissues. When subjected to increasing loads, these materials may initially exhibit elastic deformation, where the stress-strain relationship is approximately linear. However, as the load continues to increase, the material's response becomes non-linear, and the stress-strain curve deviates from a straight line. This non-linearity can be attributed to several factors, such as the material's microstructure, internal friction, and the presence of defects or impurities.

One common example of non-linear behavior is seen in materials with a highly crystalline structure, such as metals. In these materials, the atoms are arranged in a regular pattern, and the deformation process involves the movement and rearrangement of these atoms. As the material is subjected to stress, the atoms may slide past each other, leading to plastic deformation. During this process, the material's response becomes non-linear, and the stress-strain curve exhibits a characteristic hysteresis loop, where the material deforms more easily in one direction than the other.

Another factor contributing to non-linear behavior is the presence of internal friction within the material. Friction forces can oppose the applied load, causing the material to deform more slowly and leading to a non-linear stress-strain relationship. This effect is particularly significant in polymers and amorphous materials, where the molecular structure lacks the long-range order found in crystalline materials. The amorphous nature of these materials results in a higher degree of internal friction, making their stress-strain behavior non-linear.

Understanding non-linear behavior is crucial in engineering and material science, as it affects the design and performance of structures and components. Engineers must consider the non-linear properties of materials when analyzing stress distributions, predicting material failure, and selecting appropriate materials for specific applications. By recognizing and accounting for non-linear behavior, scientists and engineers can ensure the safe and efficient use of materials in various industries.

Temperature Effects: Temperature can influence material behavior, potentially affecting Hooke's Law validity

Temperature plays a significant role in the behavior of materials and can have a profound impact on the validity of Hooke's Law, which describes the linear relationship between force and displacement in elastic materials. This fundamental principle in physics is often used to understand the relationship between stress and strain in various substances. However, the law's applicability can be compromised when temperature is a variable.

As temperature increases, the kinetic energy of the particles within a material also increases. This heightened energy can lead to changes in the material's structure and properties. For instance, in metals, elevated temperatures can cause atoms to vibrate more vigorously, leading to a decrease in the material's stiffness. This effect is particularly noticeable in materials with strong temperature dependencies, such as certain alloys and polymers. As a result, the material's elastic modulus, a key parameter in Hooke's Law, may vary with temperature, making it challenging to maintain a consistent linear relationship between force and displacement.

The temperature-induced changes in material behavior can be explained by the concept of thermal expansion. When a material is subjected to higher temperatures, its atoms or molecules expand, causing the material to lengthen and become less rigid. This expansion can alter the material's response to external forces, making it less predictable and potentially deviating from Hooke's Law. For example, rubber, a material known for its elasticity, exhibits significant thermal expansion, which can affect its elastic properties and the accuracy of Hooke's Law predictions.

In scientific experiments and engineering applications, it is crucial to consider temperature effects to ensure accurate measurements and reliable predictions. Researchers and engineers often employ various techniques to minimize temperature-related variations. These methods include using temperature-controlled environments, applying thermal compensation techniques, or selecting materials with minimal temperature sensitivity. By addressing these temperature influences, it becomes possible to maintain the validity of Hooke's Law and make more accurate assessments of material behavior under different thermal conditions.

In summary, temperature is a critical factor that can challenge the applicability of Hooke's Law. The increased kinetic energy and thermal expansion associated with higher temperatures can alter material properties, making it essential to account for these effects in scientific and engineering contexts. Understanding and mitigating temperature-related variations are key to ensuring the accurate application of Hooke's Law and the reliable prediction of material behavior across a range of thermal conditions.

Frequently asked questions