Kepler's three laws of planetary motion describe how planetary bodies orbit the Sun. Kepler's third law states that the square of a planet's orbital period is proportional to the cube of the length of the semi-major axis of its orbit. However, this law does not directly apply to moons orbiting a planet, as the total mass of the two bodies involved in the moon's orbit is much smaller than the mass of the Sun-plus-planet system. As a result, the constant of proportionality in Kepler's third law is different for moons. Nevertheless, with minor modifications, Kepler's three laws can be applied to describe the motion of moons around their host planets.
| Characteristics | Values |
|---|---|
| Kepler's Third Law | The square of the period of a planet's orbit is proportional to the cube of its semimajor axis |
| Kepler's Third Law application | Kepler's Third Law applies to the motion of planets around the Sun |
| Kepler's Third Law and mass | The constant in Kepler's Third Law depends on the total mass of the two bodies involved |
| Kepler's Third Law and the Moon | Kepler's Third Law does not apply to the Moon's orbit around the Earth because the total mass of the Moon and the Earth is much smaller than the mass of the Sun |
| Kepler's Third Law and Jupiter's moons | Kepler's Third Law applies to Jupiter and its moons |
What You'll Learn

The law depends on the mass of the body being orbited
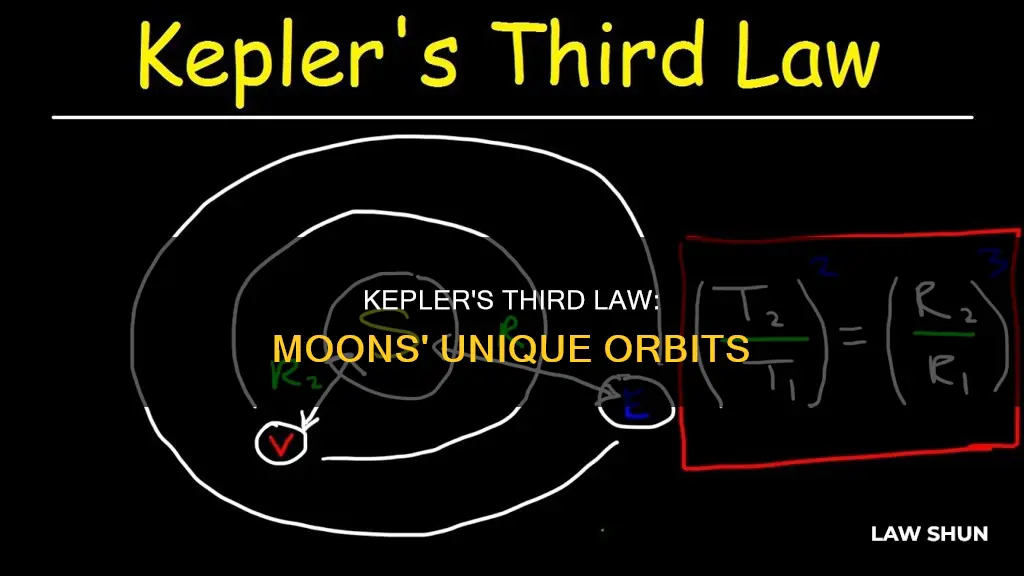
Kepler's Third Law states that the square of the period of a planet's orbit is proportional to the cube of its semi-major axis. However, this law depends on the mass of the body being orbited. The constant in Kepler's Third Law is dependent on the total mass of the two bodies involved.
For example, in the case of the Moon's orbit around the Earth, the total mass of the two bodies is much smaller than the mass of the Sun-plus-planet. This means that the value of the constant of proportionality in Kepler's Third Law will also be different. On the other hand, if we compared the period and semi-major axis of the orbit of the Moon around the Earth to the orbit of a communications satellite around the Earth, we would have almost the same total mass in each case, and thus the same relationship between period-squared and semi-major-axis-cubed.
Therefore, Kepler's Third Law can be written as:
> The constant k in the equations above is known as the Gaussian gravitational constant. If we set up a system of units with semi-major axis a in AU and mass Mtot in solar masses, then we can determine k very precisely and very simply: just count the days in a year!
The key point is that the only measured quantity needed to find k is time: the period of the Earth's orbit around the Sun. This can be determined very accurately by averaging over many years, and thus the value of k can also be determined to many significant figures.
Kepler's Third Law can be applied to stars. By measuring the period of the orbit, the semi-major axis of the orbit, and the distance to the star, the total mass of the star system can be determined in units of the solar mass.
Michelle's Law: Still Relevant or Outdated?
You may want to see also

The law applies to the moon's orbit around the Earth
Kepler's laws of planetary motion describe the orbits of planets around the Sun. However, with some minor modifications, they can also be applied to the Moon's orbit around the Earth.
Kepler's first law states that the orbit of a planet is an ellipse with the Sun at one of the two foci. In the case of the Moon, this translates to the Moon's orbit being an ellipse with the Earth at one focus. This was confirmed by Kepler himself in 1621 and later by Godefroy Wendelin in 1643.
The Moon's orbit is nearly elliptical, with an eccentricity of 0.055. The most significant perturbations to its elliptical orbit are caused by the Sun and the fact that the Earth is not a perfect sphere. Other planets and tides also have an impact on the Moon's orbit.
Kepler's second law states that a line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time. This law explains how planetary velocities vary. When a planet is closer to the Sun, it travels faster.
Kepler's third law states that the square of a planet's orbital period is proportional to the cube of the length of the semi-major axis of its orbit. This captures the relationship between the distance of planets from the Sun and their orbital periods.
These three laws can be applied to the Moon's orbit around the Earth by substituting 'Earth' for 'Sun' and 'Moon' for 'planet'. Kepler's first law describes the shape of the Moon's orbit, the second law explains how the Moon's speed varies at different points in its orbit, and the third law allows for a comparison of the Moon's orbit with that of other satellites, such as the Space Station.
Applying Natural Law: A Guide to Morality and Justice
You may want to see also

The law applies to Jupiter and its moons
Kepler's laws of planetary motion, published by Johannes Kepler in 1609, describe the orbits of planets around the Sun. Kepler's third law states that the square of a planet's orbital period is proportional to the cube of the length of the semi-major axis of its orbit.
In 1621, Kepler noted that his third law also applies to the four brightest moons of Jupiter. This was also observed by Godefroy Wendelin in 1643. Kepler's third law applies to Jupiter and its moons because the moons' orbits are elliptical, with the centre of Jupiter as one of the two foci.
The application of Kepler's third law to Jupiter and its moons was a major success for his theory. However, it is important to note that the correctness of Kepler's third law depends on the masses of the bodies involved. The law holds true for all planets orbiting the Sun and for all moons orbiting Jupiter, but not across different gravity wells.
Starlings' Law: Understanding Regurgitation in Birds
You may want to see also

The law applies to any two bodies in orbit around each other
Kepler's laws of planetary motion, published by Johannes Kepler in 1609, describe the orbits of planets around the Sun. Kepler's third law states that the square of a planet's orbital period is proportional to the cube of the length of the semi-major axis of its orbit. In other words, the ratio of the square of an object's orbital period with the cube of the semi-major axis of its orbit is the same for all objects orbiting the same primary body.
Kepler's third law applies to any two bodies in orbit around each other. This includes the Moon's orbit around the Earth, as well as Jupiter's moons orbiting Jupiter. In fact, Kepler himself noted in 1621 that his third law applies to the four brightest moons of Jupiter. However, it is important to note that the constant of proportionality in Kepler's third law depends on the total mass of the two bodies involved. Therefore, when applying Kepler's third law to moons or other bodies orbiting a planet, the constant will be different from the constant used for planets orbiting the Sun. This is because the total mass of a planet and its moon is much smaller than the mass of the Sun.
To apply Kepler's third law to moons or other bodies orbiting a planet, one must use consistent units for the measurements. The semi-major axis should be measured in Astronomical Units (AU), the mass in solar masses, and the orbital period in years. By doing so, one can calculate the Gaussian gravitational constant, which is closely related to the Newtonian Constant of Universal Gravitation. This constant can then be used to calculate very accurate planetary orbits, as demonstrated by Adams and Leverrier in their computations of Neptune.
Case Law: Michigan or Florida?
You may want to see also

The law can be used to measure the mass of a distant star
Kepler's Third Law states that the square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit. The law can be used to measure the mass of a distant star by measuring the period of the orbit, in days, and the semi-major axis of the orbit, in astronomical units (AU). This is because the constant in Kepler's Third Law depends on the total mass of the two bodies involved.
The law can be applied to stars by measuring the period and semi-major axis of a planet orbiting a distant star. This will determine the total mass of the system, including the star and the planet, in units of the solar mass. This is because the laws of physics are universal, and therefore the statement should be valid for every planetary system.
For example, in 1643, Godefroy Wendelin noted that Kepler's Third Law is fulfilled not only by planets but also by Jupiter's moons. This is because Kepler's Third Law describes the motion of any two bodies in gravitational orbits around each other.
Cars Covered by Lemon Law: What You Need to Know
You may want to see also
Frequently asked questions
Kepler's Third Law applies to moons, but only when considering the moon and the body it is orbiting as a two-body system. The constant in Kepler's Third Law depends on the total mass of the two bodies involved. When considering moons, the total mass of the moon and the body it is orbiting is much smaller than the mass of the Sun, so the value of the constant of proportionality will be different.
Kepler's Third Law can be applied to moons outside of our solar system, but only if the period of the orbit, the semi-major axis of the orbit, and the distance to the star are accurately measured. Small errors in these measurements can lead to large uncertainties in the calculated mass of the star.
Kepler's Third Law can apply to moons orbiting planets other than Earth, but only if the masses of the moon and the planet are measured accurately. The masses must be measured in solar masses, where one solar mass is 1.99 x 10^33 grams or 1.99 x 10^30 kilograms.







