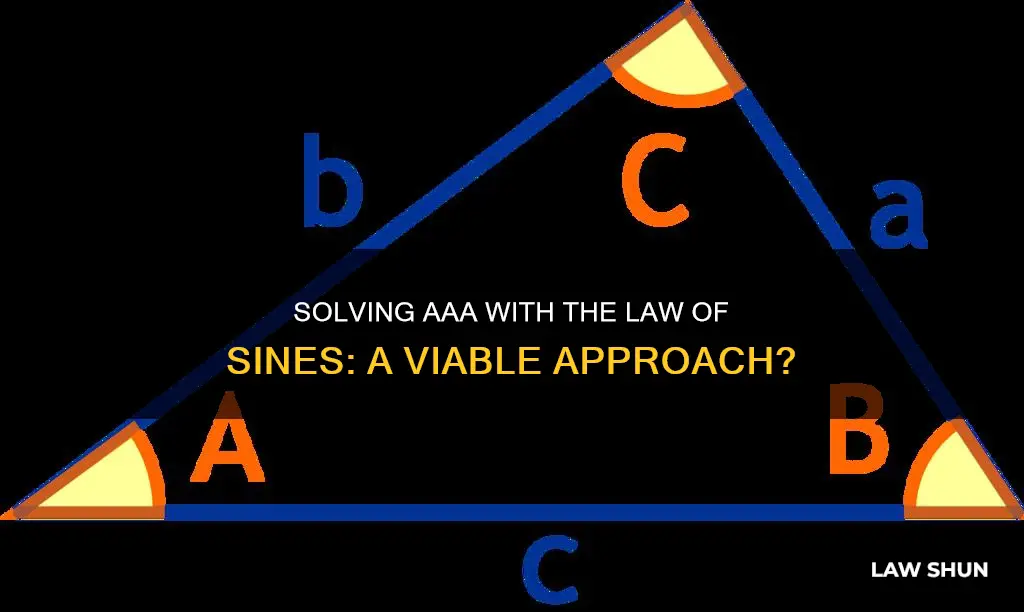
The law of sines is a trigonometric principle used to solve for unknown sides or angles in triangles. It establishes the relationship between the sides and angles of a triangle, and can be used to find the length of a side or the measure of an angle. The law of sines can be used to solve for a triangle when you know either two angles and one side (AAS) or one side and the two adjacent angles (ASA). In these cases, the remaining sides and angles can be found. However, the law of sines cannot be used when you have two sides and the included angle (SAS) or three sides (SSS).
| Characteristics | Values |
|---|---|
| Application | Finding the missing side or angle of a triangle |
| Application | Calculating the length of the side of a triangle using ASA or AAS criteria |
| Application | Calculating the unknown angle of a triangle |
| Application | Calculating the area of the triangle |
| Formula | sinAa=sinBb=sinCc |
| Formula | a/sinA = b/sinB = c/sinC |
| Formula | \(\frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c}\) |
| Conditions for application | Angle-Angle-Side (AAS) |
| Conditions for application | Angle-Side-Angle (ASA) |
| Conditions for non-application | Side-Angle-Side (SAS) |
| Conditions for non-application | Side-Side-Side (SSS) |
What You'll Learn

AAA and the law of cosines
The law of sines and the law of cosines are important rules used for solving triangles. The law of sines establishes the relationship between the sides and angles of a non-right triangle. The sine rule states that the ratios of the side lengths of a triangle to the sine of their respective opposite angles are equal.
The law of sines can be used to find the missing side or angle of a triangle, given the other requisite data. For example, if the side lengths of triangle ABC are a = 18 and b = 20 with ∠A opposite to 'a' measuring 26º, we can calculate the measure of ∠B opposite to 'b' using the sine rule: sinA/a = sinB/b = sin26º/18 = sin B/20.
The law of cosines is useful for solving a triangle when all three sides or two sides and their included angle are given. The theorem can be used to find the third side of a triangle if two sides and the angle between them or two sides and an angle opposite to one of them are known. This can also be found by two applications of the law of sines.
The law of cosines was used for solving triangles in the course of solving astronomical problems by al-Bīrūnī in the 11th century and Johannes de Muris in the 14th century. The 13th-century Persian mathematician Naṣīr al-Dīn al-Ṭūsī described how to solve triangles from various combinations of given data. Given two sides and their included angle in a scalene triangle, he proposed finding the third side by dropping a perpendicular from the vertex of one of the unknown angles to the opposite base, reducing the problem to finding the legs of a right triangle from a known angle and hypotenuse using the law of sines.
Common Law and Federal Jurisdiction: A Complex Relationship
You may want to see also

AAA and the sine rule
The law of sines, or the sine rule, is a trigonometric principle used to solve for unknown sides or angles in triangles. It establishes the relationship between the sides and angles of a non-right triangle (or an oblique triangle).
The sine rule can be applied to find the missing side or angle of a triangle when the other requisite data is known. This means that the sine rule can be used to solve for two angles and a side (AAS or AAA) or two sides and an opposite angle (SSA). For example, if side lengths of a triangle are given as a = 18 and b = 20, with angle A opposite to 'a' measuring 26º, we can calculate the measure of angle B opposite 'b' using the sine rule: sinA/a = sinB/b = sin26º/18 = sinB/20.
The law of sines can also be used to find the area of a triangle. It is expressed as:
> a/sinA = b/sinB = c/sinC
Where:
- A, b, and c are the lengths of the sides of the triangle
- A, B, and C are the angles opposite those sides
For example, if ∠A = 47º, ∠B = 78º, and side c = 6.3, we can find the length of side a using the sine rule:
> a/sinA = b/sinB = c/sinC ⇒ a/sinA = c/sinC ⇒ a/sin47º = 6.3 / sin55º ⇒ a = 6.3 / sin55º × sin47º ⇒ a = 5.6
The law of sines can be used to solve for AAA (Angle-Angle-Angle) in a triangle, as it provides the relationship between the sides and angles of a triangle. However, it is important to note that there might be two possible solutions when applying the sine rule, as two different triangles can be created using the given information.
Medical vs Law Enforcement: Who Has the Upper Hand?
You may want to see also

Finding the missing side
The law of sines is a trigonometric principle used to find unknown sides or angles in triangles. It establishes a relationship between the sides and angles of a triangle, specifically an oblique triangle or a non-right triangle. The law of sines can be used to find the missing side of a triangle when the angle-angle-side (AAS) or angle-side-angle (ASA) values are known.
The law of sines formula is expressed as:
SinAa=sinBb=sinCc
Where a, b, and c are the lengths of the triangle's sides, and A, B, and C are the angles opposite those sides. This means that the ratio of the length of a side of a triangle to the sine of the angle opposite that side is constant.
For example, let's say we have a triangle with the following values:
Angle A = 47 degrees
Angle B = 78 degrees
Side c = 6.3 units
We want to find the length of side a. Using the law of sines formula, we can set up the following equation:
A/sin(A) = b/sin(B) = c/sin(C)
Substituting the given values, we get:
A/sin(47) = 6.3 / sin(55)
To solve for 'a', we multiply both sides by sin(47):
A = 6.3 / sin(55) x sin(47)
A = 5.6
Therefore, the length of side 'a' is approximately 5.6 units.
It's important to note that the law of sines may result in two possible solutions for a triangle when using certain configurations of angles and sides. This is known as the ambiguous case. For example, if we have a triangle with Angle A = 50 degrees, side 'a' = 18 units, and side 'b' = 20 units, there will be two possible solutions for the triangle.
Fighting Corruption: Law's Limitations
You may want to see also

Finding the missing angle
The law of sines is a trigonometric principle used to solve for unknown sides or angles in triangles. It establishes the relationship between the sides and angles of a non-right triangle (also known as an oblique triangle). The law of sines can be applied to find the missing angle of a triangle when certain conditions are met. These conditions are known as AAS (Angle-Angle-Side) and ASA (Angle-Side-Angle).
In the case of AAS, you need to know two angles and one side of the triangle to find the missing angle. For example, let's say you have a triangle with angles A = 50°, B = 60°, and side a = 60. To find the missing angle C, you can use the law of sines formula: sin(A)/a = sin(B)/b = sin(C)/c. By substituting the known values, you can solve for the sine value of angle C. Once you have sin(C), you can find the angle itself by taking the inverse sine (arcsin) of both sides, resulting in angle C.
For ASA, you need to know one side and the two adjacent angles. For instance, consider a triangle with side a = 10, angle A = 20°, and angle B = 110°. To find the missing angle C, you can again use the law of sines formula: sin(A)/a = sin(B)/b = sin(C)/c. With the known values, you can calculate sin(C), and then find angle C by taking the inverse sine.
It's important to note that the law of sines may result in an ambiguous case, where there are two possible solutions for the triangle. This occurs when you have information about angle A, side a, and side c, with angle A being acute (less than 90°), side a shorter than side c, and side a longer than the altitude h from angle B. In such cases, both solutions should be considered valid.
Additionally, the law of sines can be applied to both right triangles and oblique triangles. However, it cannot be effectively used with SAS (Side-Angle-Side) or SSS (Side-Side-Side) triangle configurations. For these cases, the law of cosines is typically employed instead.
Martial Law: Elections Cancelled?
You may want to see also

The ambiguous case
The law of sines establishes the relationship between the sides and angles of an oblique triangle (non-right triangle). It can be used to calculate the length of a side of a triangle, the unknown angle of a triangle, or the area of the triangle.
When applying the law of sines to solve a triangle, there might be a case when there are two possible solutions. This occurs when two different triangles can be created using the given information. This is known as the ambiguous case.
For example, let's consider the following triangle: \(\angle A=38^{\circ}\), side a = 40, and side b = 24. Using the law of sines, we can calculate the possible values for angle C. In the first possibility, \(\angle C\) would be approximately \(15.2^{\circ}\). In the second possibility, \(\angle C\) would be approximately \(88.8^{\circ}\). To find the two possible lengths for side c, we need to solve two law of sines calculations, one for each possible value of \(\angle C\).
It's important to note that the ambiguous case in the law of sines arises due to the periodic nature of trigonometric functions, where sine and cosine values repeat at regular intervals. This can result in multiple solutions when using inverse trigonometric functions to find angles or sides in a triangle.
Daughter-in-Law's Legal Rights to Ancestral Property
You may want to see also
Frequently asked questions
The law of sines is a mathematical principle used to solve for unknown sides or angles in triangles. It establishes the relationship between the sides and angles of a non-right triangle.
The law of sines can be used to solve a triangle when you know either two angles and one side (AAS) or one side and the two adjacent angles (ASA).
Side-Angle-Side (SAS) and Side-Side-Side (SSS) configurations cannot be solved using the law of sines.
Sure, let's use the example of solving ∆ABC where A = 50°, a = 60, and b = 40. First, we need to find the third angle. Then, we can use the law of sines to find the third side.