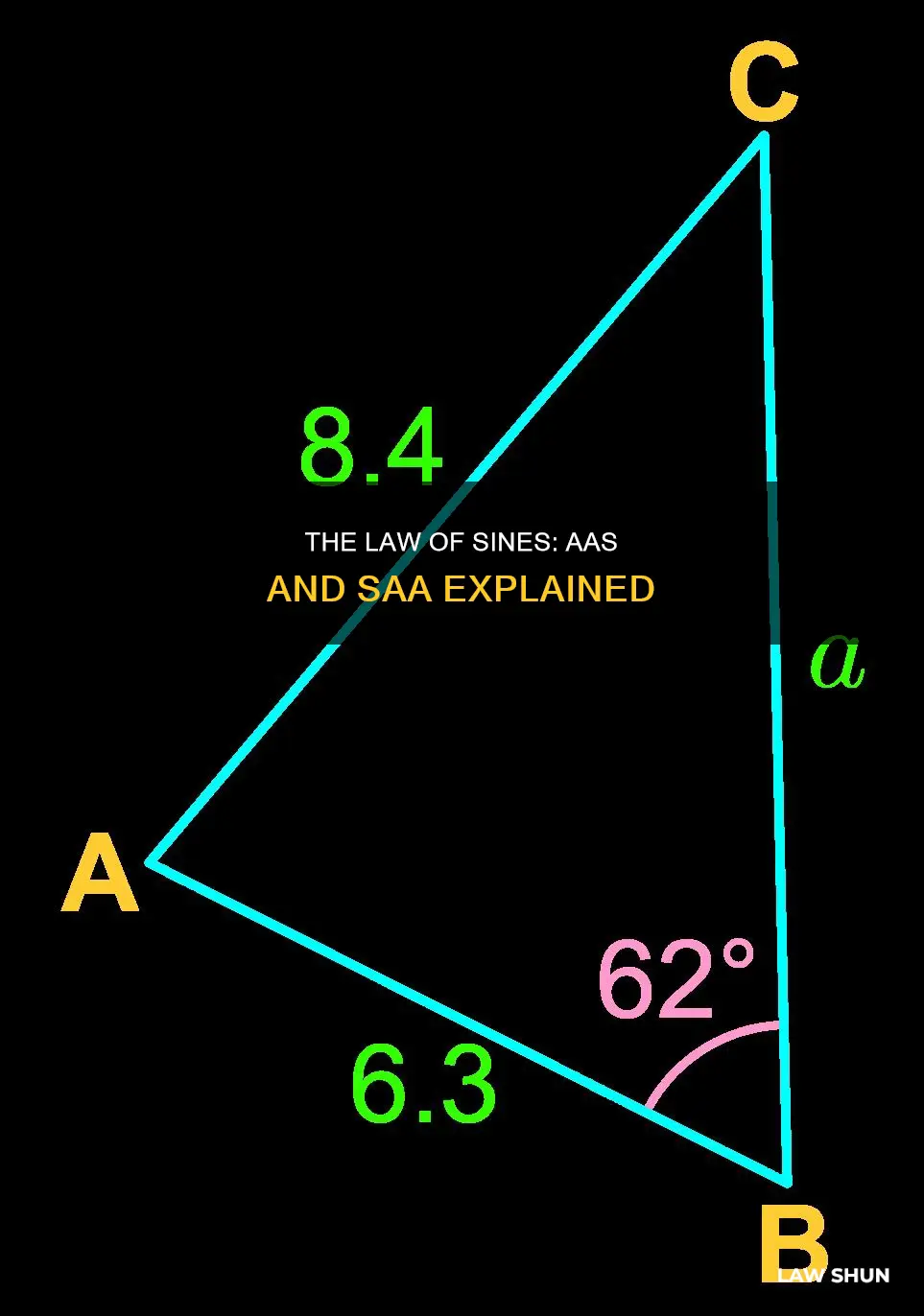
The law of sines is used to find the unknown angle or side of a triangle. This law can be used if certain combinations of measurements of a triangle are given. AAS criteria: given two angles and a non-included side, to find the unknown side. The law of sines can be used when we have AAS (angle-angle-side) criteria. However, it is not clear what SAA criteria would be and whether it would be applicable to the law of sines.
| Characteristics | Values |
|---|---|
| AAS criteria | Two angles and a non-included side are known, and the unknown side needs to be found |
| ASA criteria | Two angles and the included side are known, and the unknown side needs to be found |
| SSA criteria | Two sides and a non-included angle are known, and there is a possibility of 0, 1, or 2 triangles with this combination |
What You'll Learn

AAS criteria for the law of sines
The law of sines is used to find the unknown angle or side of a triangle, specifically an oblique triangle, which is defined as any triangle that is not a right triangle. The law of sines can be applied when we have ASA (Angle-Side-Angle) or AAS (Angle-Angle-Side) criteria.
The AAS criteria for the law of sines can be used to find the unknown side of a triangle when we know two angles and a non-included side. For instance, if we know the lengths of sides a and c, and the measure of angle A, we can use the law of sines to find the length of side b.
The sine rule states that the ratio of the side lengths of a triangle to the sine of their respective opposite angles are equal. This means that side "a" divided by the sine of angle A is equal to side "b" divided by the sine of angle B, which is equal to side "c" divided by the sine of angle C.
The law of sines can be used in real life for measuring the angle of tilt in engineering, measuring the distance between planets or stars in astronomy, and for navigation.
HOA's Power: Can They Limit New Airbnb Laws?
You may want to see also

ASA criteria for the law of sines
The law of sines is used to find the unknown angle or side of a triangle. This law can be used if certain combinations of measurements of a triangle are given. The ASA criteria, which stands for angle-side-angle, can be used to find the unknown side of a triangle when two angles and the included side are known.
The law of sines defines the ratio of sides of a triangle to their respective sine angles. This means that the sides of a triangle are proportional to the sines of their opposite angles. This relationship is established by the sine rule, which states that the ratio of the side lengths of a triangle to the sine of their respective opposite angles are equal. This rule can be used to find the missing angle or side of any triangle using the known data.
The law of sines can be used to solve oblique triangles, which are triangles that are not right triangles. In order to solve any triangle, you need to know the length of at least one side and two other parts. For an oblique triangle, the law of sines or the law of cosines must be used. The sine law can also be used for right triangles.
The ASA criteria is one of two methods that can be used with the law of sines, the other being the AAS criteria. The AAS criteria, or angle-angle-side, can be used to find the unknown side of a triangle when two angles and a non-included side are known. Both the ASA and AAS methods will provide a unique solution and are used to prove the congruence of triangles.
Congress' Law-Making Power Without Presidential Signature
You may want to see also

SSA criteria for the law of sines
The law of sines is used to solve oblique triangles when two angles and one side are known (ASA or AAS) or when two sides and an opposite angle are known (SSA). In the case of SSA triangles, we are given two sides of a triangle and an angle that is opposite to one of the sides. This is also known as a Side-Side-Angle triangle.
SSA triangles are considered an ambiguous case because when two sides and a non-included angle are known, there is a possibility of 0, 1, or 2 triangles with that combination of sides and angles. To solve an SSA triangle, the first step is to calculate the number of triangles for the combination of sides and angles.
For example, let's consider a triangle where angle M = 125°, m = 12.4, and l = 7.6. We can use the Law of Sines to find angle L. In this case, there is only one answer, as the other possible answer for L is 149.9°, which is impossible because a triangle cannot have two angles greater than 90°.
Another example is a triangle where A=110°, a=58, and b=67. This is an SSA triangle, and since angle A is obtuse, and side a is shorter than side b, we can conclude that no triangle exists.
Martial Law: Can a Single State Take Control?
You may want to see also

Law of sines for right triangles
The law of sines is used to find the unknown angle or side of a triangle. This law can be used if certain combinations of measurements of a triangle are given. The law of sines defines the ratio of sides of a triangle and their respective sine angles are equivalent to each other. It is also called the sine rule, sine law, or sine formula.
The law of sines can be used when we have ASA (angle-side-angle) or AAS (angle-angle-side) criteria. ASA criteria refer to when we are given two angles and the included side, and we want to find the unknown side. AAS criteria refer to when we are given two angles and a non-included side, and we want to find the unknown side.
The formula for the law of sines is:
$$\\frac{\\sin A}{a} = \\frac{\\sin B}{b} = \\frac{\\sin C}{c}$$
This formula can be used to find the unknown sides of a right triangle if two angles and one side are known. It can also be used to find the third side of a right triangle if two sides and one of the non-enclosed angles are known.
In some cases, there may be two solutions to the same triangle, known as ambiguous cases. To avoid this, it is important to calculate the number of triangles possible with the given combination of sides and angles.
HOA's Power: Restricting New Airbnb Laws in Condos
You may want to see also

Law of sines for oblique triangles
The Law of Sines, also known as the Sine Rule, is a formula that allows us to make calculations based on the angles of triangles rather than their sides. It is used to solve oblique triangles, or non-right triangles, and can be used to find unknown sides and values. The formula is represented as:
$$\\frac{\\sin A}{a} = \\frac{\\sin B}{b} = \\frac{\\sin C}{c}$$
Where A, B, and C are the angles of the triangle, and a, b, and c are the sides of the triangle. The lower-case letters represent the sides of the triangle, while the upper-case letters represent the angles.
To use the Law of Sines, an angle and its opposite side must be known. This allows us to find the other sides and angles of the triangle. For example, let's say we have a triangle with angle A = 20°, angle B = 60°, and side a = 10. We can use the Law of Sines to find the other sides, b and c.
$$\\frac{\\sin 20^\circ}{10} = \\frac{\\sin 60^\circ}{b} = \\frac{\\sin C}{c}$$
We can solve for b and c to find the other sides of the triangle. It is important to note that in some cases, the Law of Sines may result in ambiguous solutions, where more than one triangle satisfies the given criteria.
DACA Recipients and Their Legal Practice in Texas
You may want to see also
Frequently asked questions
AAS stands for Angle-Angle-Side.
The Law of Sines is used to find the unknown angle or side of a triangle. It is also known as the Sine Rule, Sine Law or Sine Formula.
The formula for the Law of Sines is: side a / sin(angle A) = side b / sin(angle B) = side c / sin(angle C).
No, AAS and SAA are different. AAS refers to Angle-Angle-Side, while SAA refers to Side-Angle-Angle.







