De Morgan's Laws are two statements that describe the interactions between various set theory operations. They are named after Augustus De Morgan, who introduced a formal version of the laws to classical propositional logic. De Morgan's Laws can be applied to both elementary algebra and Boolean algebra. In the context of probability, De Morgan's Laws can be used to calculate the probability of multiple things not happening. For example, when calculating the probability of two things not happening, De Morgan's Laws state that the probability is equal to one minus the sum of the probabilities of the two individual events. This application of De Morgan's Laws in probability theory is based on the assumption that probabilities are independent.
| Characteristics | Values |
|---|---|
| De Morgan's Laws | Describe how mathematical statements and concepts are related through their opposites |
| First Law | The complement of the union of two sets is the intersection of their complements |
| Second Law | The complement of the intersection of two sets is the union of their complements |
| Application | Can be applied to set theory, boolean algebra, elementary algebra, computer engineering, digital circuit design, formal logic, and probability theory |
| Visualization | Can be easily visualized using Venn diagrams |
What You'll Learn

De Morgan's Laws and set theory
De Morgan's laws are a pair of transformation rules in Boolean algebra and set theory that relate the intersection and union of sets through complements. In set theory, there are two De Morgan's laws:
First De Morgan's Law
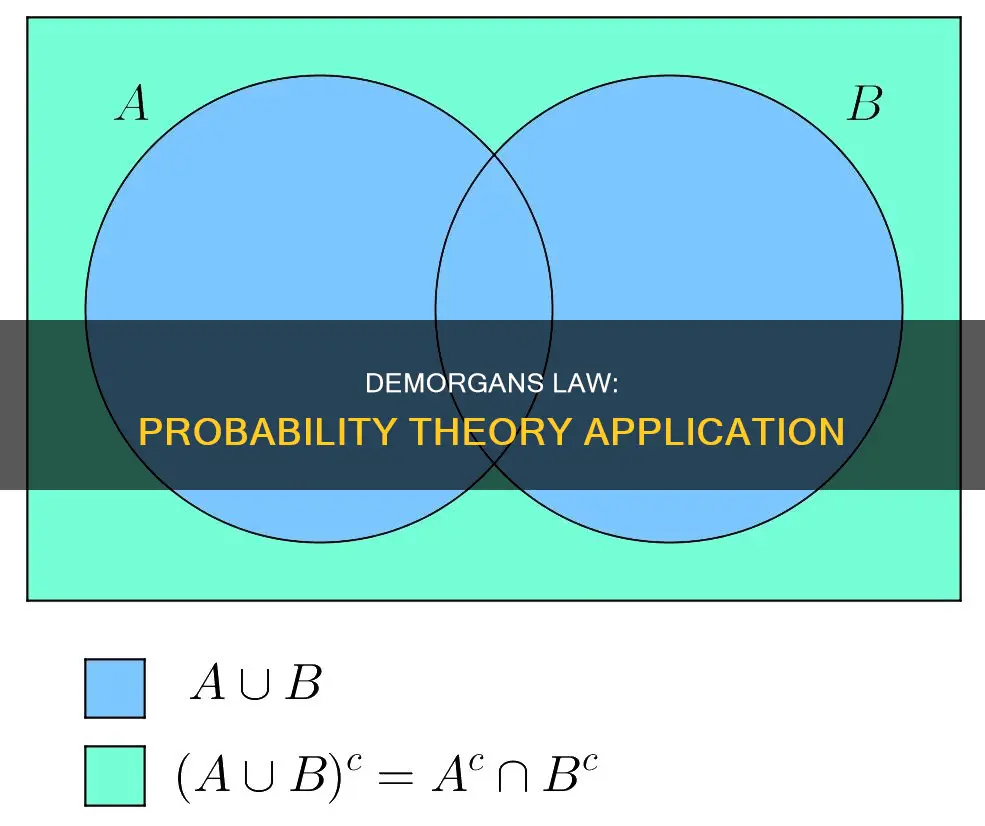
The first law states that the complement of the union of two sets is equal to the intersection of the complements of each set. This is also known as De Morgan's Law of Union and can be represented as:
> (A ∪ B)’ = A’ ∩ B’
Second De Morgan's Law
The second law states that the complement of the intersection of two sets is equal to the union of the complements of each set. This is also known as De Morgan's Law of Intersection and can be represented as:
> (A ∩ B)’ = A’ ∪ B’
These laws can be generalized to any number of sets and can be easily visualized using Venn diagrams. De Morgan's laws are used to simplify mathematical expressions and are critical in understanding mathematical arguments. They are also used in computer engineering for developing logic gates and in digital circuit design.
De Morgan's laws can also be applied to probability. For example, when calculating the probability of multiple things not happening, De Morgan's laws can be used to relate the intersection and union of sets through complements.
Criminal Law Powers: Can Cities Legislate?
You may want to see also

De Morgan's Laws in probability calculations
De Morgan's Laws describe how mathematical statements and concepts are related through their opposites. In set theory, De Morgan's Laws relate the intersection and union of sets through complements. In propositional logic, De Morgan's Laws relate conjunctions and disjunctions of propositions through negation.
De Morgan's Laws can be applied to probability calculations. For example, when calculating the probability of multiple things not happening, De Morgan's Laws can be used to represent the relationship between the probabilities.
$$ \prod_{n=1}^{k}\left(1-P\left(n\right)\right)=1-\sum_{n=1}^{k}\left(P\left(n\right)\right) $$
The first part of the equation, $\prod_{n=1}^{k}\left(1-P\left(n\right)\right)$, represents the probability of none of the events $n$ occurring, which is equal to $1$ minus the sum of the probabilities of each event $n$ occurring, represented by the second part of the equation, $1-\sum_{n=1}^{k}\left(P\left(n\right)\right)$.
De Morgan's Laws can also be generalized to any number of sets. For example, let $\{A_1,\ A_2,\ ...,\ A_{n-1},\ A_n\}$ be a set of $n$ sets. The complement of the intersection of these sets is:
$$ \left(\bigcap\limits_{k=1}^n{A_k}\right)^c=\bigcup\limits_{k=1}^n{A_k^c} $$
The $\bigcap$ and $\bigcup$ symbols represent the intersection and union of many sets, respectively.
De Morgan's Laws are useful in probability calculations as they allow us to simplify complex probability expressions and make valid inferences in proofs and deductive arguments. They are also applicable in other fields, such as computer engineering and computer programming, where they are used for developing logic gates and manipulating the types of logic gates, respectively.
Congressional Powers: Overriding State Laws?
You may want to see also

Boolean algebra and De Morgan's Laws
De Morgan's Laws describe how mathematical statements and concepts are related through their opposites. In set theory, De Morgan's Laws relate the intersection and union of sets through complements. In propositional logic, De Morgan's Laws relate conjunctions and disjunctions of propositions through negation. De Morgan's Laws are also applicable in computer engineering for developing logic gates.
De Morgan's Laws can be generalized to any number of sets. The first De Morgan Law in set theory states that the complement of the union of two sets is equal to the intersection of their individual complements. In other words, "Not (A or B)" is the same as "Not A and Not B".
The second De Morgan Law in set theory states that the complement of the intersection of two sets is equal to the union of their individual complements. So, "Not (A and B)" is the same as "Not A or Not B".
In Boolean algebra, De Morgan's Laws define the relation between the OR, AND, and the complements of variables, and is given for both the complement of AND and OR of two values. In Boolean Algebra, De Morgan's Laws can be used to find the equivalency of the NAND and NOR gates.
De Morgan's Laws are also applicable in computer engineering for developing logic gates. They can be used to simplify or properly negate complicated logical conditions. They are also often useful in computations in elementary probability theory.
How Congress Can Pass Laws Without Senate Approval
You may want to see also

De Morgan's Laws in computer engineering
De Morgan's Laws, named after 19th-century British mathematician Augustus De Morgan, are a pair of transformation rules that are valid rules of inference. They are used in computer engineering, especially in the development of logic gates, digital circuit design, and algorithms and programming.
In computer engineering, De Morgan's Laws are commonly written as:
- The complement of the conjunction of two variables equals the disjunction of their complements.
- The complement of the disjunction equals the conjunction of their complements.
These laws are fundamental principles in Boolean algebra and set theory, providing rules for transforming logical expressions. They are essential for simplifying and manipulating Boolean expressions, which have significant applications in digital circuit design, computer science, and engineering.
De Morgan's Laws can be applied to the negation of a disjunction or the negation of a conjunction in all or part of a formula. For example, "it is false that either of A or B is true" is equivalent to "both A is not true and B is not true." This can be further simplified to "not A and not B."
In computer networking, De Morgan's Laws can be used to express firewall rules. For instance, a firewall rule that allows traffic that is "not from subnet A and not destined for port 80" can be expressed in terms of positive conditions using De Morgan's Laws.
Common-Law Couples: Filing Taxes Separately, Possible?
You may want to see also

De Morgan's First Law
In simple terms, De Morgan's First Law states that the negation of "A and B" is the same as "not A or not B". This can be expressed as:
> The kitchen floor needs mopping and the utensils need washing, but I will not do both = I will not mop the kitchen floor or I will not wash the utensils.
In other words, to negate an "and" statement, you negate each part and change the "and" to "or". This is often used to simplify complex expressions.
> (∩k=1nAk)c=∪k=1nAkc
Congress' Power: Can They Repeal Previous Laws?
You may want to see also
Frequently asked questions
De Morgan's Laws are two statements that describe the interactions between various set theory operations. The laws are that for any two sets A and B:
- The complement of the union of two sets is the intersection of their complements.
- The complement of the intersection of two sets is the union of their complements.
De Morgan's Laws can be applied to probability by defining the operation P(A) + P(B) = P(A) ∪ P(B) - P(A)P(B) and using ∪ instead of +. This will follow De Morgan's Laws assuming that probabilities are independent.
De Morgan's Laws are helpful in making valid inferences in proofs and deductive arguments. They are also used in computer engineering for developing logic gates and in computations in elementary probability theory.







