Understanding Beer's Law: The Significance Of E 84000

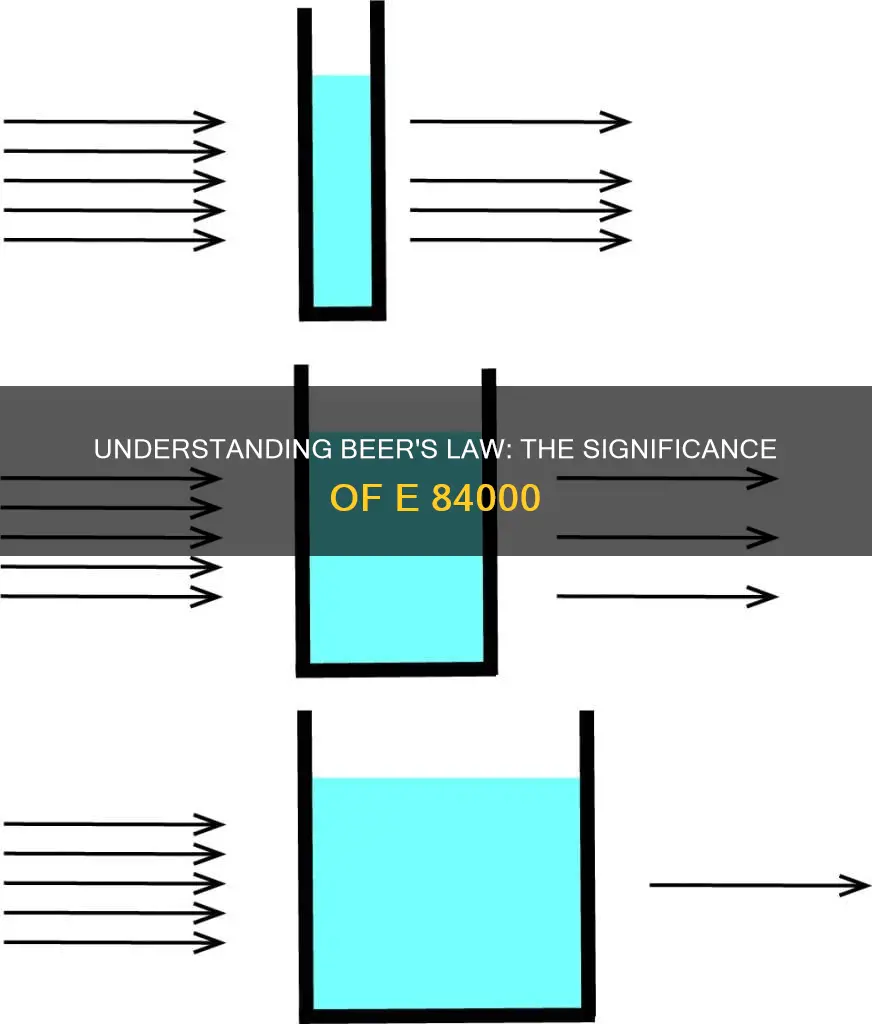
The Beer-Lambert law, commonly referred to as Beer's Law, is an empirical relationship that describes the attenuation in intensity of a radiation beam passing through a homogeneous medium. It states that the intensity of radiation decays exponentially with the absorbance of the medium, and this absorbance is directly proportional to the concentration of the solution. The law is used to determine the concentration of a chemical species in a solution and is particularly important in chemistry, physics, and meteorology. It can be applied to understand the attenuation of particle beams and has many modern-day applications in labs for testing medicines, organic chemistry, and quantification.

Beer's Law and Lambert Law

The Beer-Lambert Law, also called Beer's Law, is a relationship between the attenuation of light through a substance and the properties of that substance. It is an empirical relationship that describes the attenuation in intensity of a radiation beam passing through a macroscopically homogeneous medium with which it interacts. The law states that the intensity of radiation decays exponentially in the absorbance of the medium, and that said absorbance is proportional to the length of the beam passing through the medium, the concentration of interacting matter along that path, and a constant representing the matter's propensity to interact.

The Beer-Lambert Law is expressed as:

A=εlc

Where:

• A is the absorbance
• Ε (epsilon) is the molar absorptivity or molar extinction coefficient
• L is the length of the beam passing through the medium
• C is the concentration of interacting matter along that path

The Beer-Lambert Law is used to calculate the concentration of a solution by measuring its absorbance. The law states that there is a linear relationship between the concentration and the absorbance of the solution. The absorbance is defined via the incident intensity (I0) and transmitted intensity (I):

A=log10(I0/I)

Where:

• I0 is the incident intensity
• I is the transmitted intensity

The Beer-Lambert Law is based on the work of Beer, Bouguer, and Lambert. Beer's analysis did not discuss the prior work of Bouguer and Lambert, who studied the absorption of light in astronomical contexts. Solutions are homogeneous and do not scatter light at common analytical wavelengths, except at entry and exit. Thus, light within a solution can be approximated as due to absorption alone. In astronomical contexts, atmospheric dust or other inhomogeneities could scatter light away from the detector. Modern texts combine the two laws because scattering and absorption have the same effect.

The Beer-Lambert Law is valid under certain conditions. There are at least six conditions that need to be fulfilled for the law to be valid:

• The attenuators must act independently of each other.
• The attenuating medium must be homogeneous in the interaction volume.
• The attenuating medium must not scatter the radiation (no turbidity) unless this is accounted for.
• The incident radiation must consist of parallel rays, each traversing the same length in the absorbing medium.
• The incident radiation should preferably be monochromatic or have a narrow width.
• The incident flux must not influence the atoms or molecules; it should only act as a non-invasive probe of the species under study.

Deviations from the Beer-Lambert Law can occur due to real, chemical, or instrument factors. Real deviations are due to the limitations of the law itself, chemical deviations are observed due to specific chemical species in the sample, and instrument deviations occur due to how the attenuation measurements are made. The law tends to break down at very high concentrations, especially if the material is highly scattering.

Molar absorptivity

The Beer-Lambert law, also known as Beer's law, states that the attenuation of light is directly proportional to the properties of the material through which it is passing. These properties include the length of the beam passing through the medium, the concentration of the interacting matter, and a constant representing the matter's propensity to interact. The Beer-Lambert law can be expressed as:

> A = εlc

Where:

• A is the absorbance
• Ε is the molar absorptivity or molar extinction coefficient
• L is the length of the solution the light passes through
• C is the concentration of the solution

Beer-Lambert Law derivation

The Beer-Lambert law, also known as Beer-Bouguer-Lambert (BBL) extinction law, describes the relationship between the attenuation of light through a substance and the properties of that substance. It is a combination of Beer's law and Lambert's law, with the former being an extension of the latter.

Lambert's Law

Lambert's law, discovered by Johann Heinrich Lambert, states that the loss of light intensity when it propagates through a medium is directly proportional to the intensity of the light and the path length travelled. In other words, it establishes a quantitative relationship between the decrease in the intensity of monochromatic light passing through a homogeneous medium of thickness dx and the light intensity I. This can be expressed mathematically as:

\[\begin{equation*}

\frac{-dI}{dx} = \frac{I_0 - I}{dx}

\end{equation*}\]

Where:

• \(I_0\) is the initial light intensity
• \(I\) is the light intensity after passing through the medium
• \(x\) is the thickness of the medium

Beer's Law

Building on Lambert's work, August Beer introduced the concept of solution concentration to the law, resulting in what is now known as Beer's law. Beer's law states that the amount of light absorbed is directly proportional to the concentration of the solution. In other words, it asserts that the length of a sample route and the concentration of a solution are proportional to the light's absorbance. This can be expressed mathematically as:

\[

\begin{equation*}

A = \epsilon \ell c

\end{equation*}

\]

Where:

• \(A\) is the absorbance
• \(\epsilon\) is the molar absorption coefficient
• \(\ell\) is the path length
• \(c\) is the concentration of the solution

Beer-Lambert Law

The Beer-Lambert law combines the principles of Beer's law and Lambert's law, relating the intensity of absorbed light to the thickness of the absorbing medium and the concentration of the solution. It is expressed mathematically as:

\[

\begin{equation*}

A = \epsilon c \ell

\end{equation*}

\]

Where:

• \(A\) is the absorbance
• \(\epsilon\) is the molar absorptivity or molar absorption coefficient
• \(c\) is the concentration of the solution
• \(\ell\) is the path length

The Beer-Lambert law has numerous applications in modern-day science, particularly in chemical analysis, physical optics, and the testing of medicines and organic chemistry. However, it is important to note that the law has limitations and tends to break down at very high concentrations, especially if the material is highly scattering.

Validity of Beer-Lambert Law

The Beer-Lambert law, also known as Beer's Law, is an empirical relationship that describes the attenuation in intensity of a radiation beam passing through a macroscopically homogeneous medium with which it interacts. It is important to note that the Beer-Lambert law is based on certain assumptions and is only valid under specific conditions.

The law states that the intensity of radiation decays exponentially with the absorbance of the medium, and this absorbance is directly proportional to the length of the beam passing through the medium, the concentration of interacting matter along that path, and a constant representing the matter's propensity to interact. In simpler terms, it relates the attenuation of light to the properties of the material through which the light is travelling.

For the Beer-Lambert law to be valid, several conditions must be met. These include the requirement that the attenuators act independently of each other, and the attenuating medium must be homogeneous in the interaction volume. Additionally, the attenuating medium should not scatter the radiation, and the incident radiation should consist of parallel rays, each traversing the same length in the absorbing medium. The incident radiation is preferably monochromatic or, at the very least, narrow enough to be accommodated by the attenuating transition.

The Beer-Lambert law is commonly used in chemical analysis, where it is applied to analyse the absorption of light by a chemical solution. It is also used in physical optics, where it helps quantify astronomical extinction and the absorption of photons, neutrons, or rarefied gases.

The validity of the Beer-Lambert law has been questioned in certain scenarios, such as in the presence of high concentrations of UV absorbers in sunscreen films on human skin. However, studies have shown that the law still holds true even in these cases.

Applications of Beer-Lambert Law

The Beer-Lambert Law, also known as Beer's Law, the Lambert-Beer Law, or the Beer-Lambert-Bouguer Law, has a wide range of applications across various fields. This law relates the attenuation of light to the properties of the material through which the light is travelling. Here are some of its key applications:

Spectrophotometry and Laboratory Testing

The Beer-Lambert Law is fundamental in spectrophotometry, a technique used to separate, quantify, and identify substances within a sample. This method is applied in various laboratory settings, including the evaluation of pharmaceuticals, organic chemistry, and quantification-based studies. For example, a blood sample's bilirubin count can be determined using a spectrophotometer, and the Beer-Lambert Law helps relate the light absorption to the sample's properties.

Chemistry

Chemists use the Beer-Lambert Law to determine the concentration of chemical solutions, study oxidation reactions, and assess polymer degradation. This law allows chemists to understand how the concentration of a solution is directly related to its absorbance of light. Additionally, the law helps explain how radiation attenuates as it passes through different materials, including the Earth's atmosphere.

Physics

In the field of physics, the Beer-Lambert Law is applied to understand the behaviour of particle beams, such as neutrons, as they attenuate through materials. This law helps physicists relate the absorption and transmission of energy to the properties of the material through which the particles are travelling.

Meteorology

Meteorologists use the Beer-Lambert Law to explain the behaviour of solar and stellar radiation in the Earth's atmosphere. The law's modified equation in atmospheric applications takes into account various atmospheric components, such as T_a, T_g, T_RS, and T_NO2, to describe the transmission of radiation through the atmosphere.

Civil Engineering

The Beer-Lambert Law has applications in the development of high-performance graphene-modified asphalt (GMA). By understanding the relationship between light absorption and material properties, engineers can design asphalt with improved dispersion and composite modification effects. This leads to enhanced rutting resistance and better overall performance of asphalt pavements.

The Beer-Lambert Law, with its ability to relate light absorption to material properties, has become a valuable tool in various scientific and industrial domains, contributing to advancements in fields ranging from chemistry and physics to engineering and meteorology.

Frequently asked questions