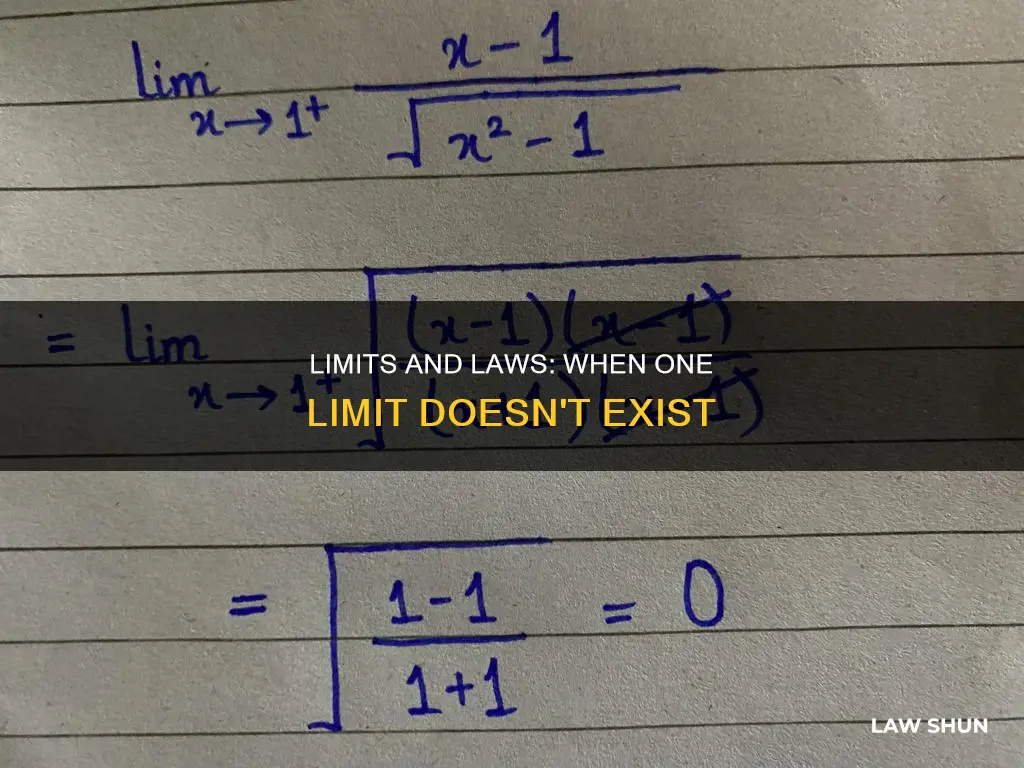
The limit laws are a set of rules that allow us to find the limits of various combinations of functions. These laws are typically presented with the assumption that both individual limits exist. However, it is possible to modify these laws to account for cases where one of the limits does not exist. This involves considering the behaviour of the functions involved and applying certain conditions. For example, if one of the functions tends to infinity while the other approaches a finite value, the product of their limits may still be determined. It is important to note that these modified limit laws require careful application, and further analysis may be needed for more complex cases.
| Characteristics | Values |
|---|---|
| Limit laws are valid | As long as they do not lead to indeterminate forms |
| Limit laws are given | On the condition that both individual limits exist |
| Limit laws can be applied | When a function is defined for all a over some open interval containing a |
| Limit laws can be applied | When the limit of the denominator is not zero |
| Limit laws can be applied | When the limit of the denominator exists |
What You'll Learn
- The limit laws are given on the condition that both individual limits exist
- Limit laws can be applied to one-sided limits
- Limit laws can be used to evaluate the limit of a polynomial or rational function
- Limit laws can be used to evaluate the limit of a function by factoring or by using conjugates
- Limit laws can be used to evaluate the limit of a function by using the squeeze theorem

The limit laws are given on the condition that both individual limits exist
In calculus, the limit laws are given on the condition that both individual limits exist. This means that, for the limit laws to be applied, the new limits must exist. For instance, the limit of x as x approaches a is a, and the limit of a constant is that constant.
The limit laws include the difference law, constant multiple law, product law, quotient law, power law, root law, and more. These laws allow us to evaluate the limit of a function, a polynomial or rational function, by factoring or by using conjugates.
However, it is important to note that the limit laws cannot always be applied. For example, if the function is not defined for a specific value or interval, the limit laws may not be applicable. In such cases, we might need to consider one-sided limits or use alternative techniques, such as L'Hospital's Rule, Taylor series, or the Squeeze Theorem.
Additionally, when dealing with products or quotients, it is crucial to ensure that the limit of one of the functions is non-zero. This is because dividing by zero is undefined.
Furthermore, while it may be tempting to abuse notation and perform arithmetic operations with infinity, this should be avoided as it can lead to incorrect results. Instead, it is recommended to work with the symbolic representation of infinity and use appropriate limit laws.
In summary, the limit laws in calculus provide a foundation for calculating many limits, but their application relies on the existence of both individual limits. When applying these laws, it is essential to carefully consider the requirements and limitations of each law to ensure accurate results.
Laws on Reservations: Who Has Jurisdiction?
You may want to see also

Limit laws can be applied to one-sided limits
> limx → a⁻ f(x)
The function f(x) must be defined over an open interval of the form:
> (a − δ, a) for some δ > 0.
Similarly, for a limit of the form:
> limx → a⁺ f(x)
The function f(x) must be defined over an open interval of the form:
> (a, a + δ) for some δ > 0.
In other words, the limit laws can be applied to one-sided limits as long as the function is defined in an open interval around the limit value. This ensures that the limit can be evaluated by considering the behaviour of the function as it approaches the limit value from one side.
It's important to note that the limit laws assume that both individual limits exist. However, in some cases, the limit laws can still be applied even if one of the limits does not exist. This is because the limit laws deal with the behaviour of the functions as they approach the limit value, rather than the specific values of the limits themselves.
For example, consider the limit law for the product of two functions:
> limx → a [f(x)⋅g(x)] = limx → a f(x) ⋅ limx → a g(x)
This law can be applied even if one of the limits, limx → a f(x) or limx → a g(x), does not exist, as long as the limit of the other function exists and the functions satisfy the required conditions in an open interval around the limit value.
In summary, while the limit laws are typically stated with the assumption that both individual limits exist, they can sometimes be applied to one-sided limits or in cases where one of the limits does not exist. However, it's important to carefully analyse the functions and their behaviour near the limit value to ensure that the conditions for applying the limit laws are met.
Antitrust Laws: Global Reach and Overseas Application
You may want to see also

Limit laws can be used to evaluate the limit of a polynomial or rational function
Limit laws are a set of rules that allow us to find the limits of various combinations of functions. These laws can be used to evaluate the limit of a polynomial or rational function.
The limit of a polynomial function can be evaluated by considering each term of the function and applying the limit laws to each term. For example, let's consider the polynomial function:
> f(x) = a0 + a1x + a2x2 + ... + anxn
The limit of this function as x approaches a can be written as:
> limxa f(x) = limxa [a0 + a1x + a2x2 + ... + anxn]
We can split the limit for each term of the function:
> limxa f(x) = limxa a0 + limxa a1x + limxa a2x2 + ... + limxa anxn
Now, we can take the coefficients out of the limit:
> limxa f(x) = a0 + a1 * limxa x + a2 * limxa x2 + ... + an * limxa xn
Applying the limit laws to each term, we get:
> limxa f(x) = a0 + a1a + a2a2 + ... + ana^n = f(a)
So, the limit of the polynomial function f(x) as x approaches a is equal to the value of the function f(x) at x = a.
For rational functions, the limit can be evaluated by first understanding the structure of the function. A function f is called a rational function if it can be written as:
> f(x) = g(x)/h(x)
Where g(x) and h(x) are polynomial functions and h(x) is not equal to 0.
The limit of the rational function f(x) as x tends to a is given by:
> limxaf(x) = limxag(x)/h(x) = [limxag(x)]/[limxah(x)] = g(a)/h(a)
However, if h(a) = 0, then we need to consider two cases to define the limit of the rational function. In this case, g(a) is not equal to 0, and h(a) is equal to 0, so the limit does not exist. We need to evaluate the functions g(x) and h(x) individually and apply the quotient rule of exponents.
In summary, limit laws can be used to evaluate the limit of a polynomial or rational function by considering the individual terms or components of the function and applying the appropriate limit laws. It's important to note that the existence of both limits is required for most limit laws to be applicable.
Fair Housing Laws: Private Landlords' Obligations and Compliance
You may want to see also

Limit laws can be used to evaluate the limit of a function by factoring or by using conjugates
Evaluating Limits
When evaluating limits, the first step is to check if the function is continuous. If the function is continuous at the point where the limit is being evaluated, simply substitute the value and solve the function.
Limit by Factoring
Limit by factoring is a method for evaluating limits that require determining and evaluating common factors. For example, to evaluate the limit:
> limy→5(y^2 − y − 20)/(y − 5)
The expression can be factored to:
> limy→5((y − 5)(y + 4))/(y − 5)
This simplifies to:
> limy→5(y + 4)
Now, we can substitute y = 5:
> limy→5(9) = 9
Limit by Conjugates
Conjugates are used when direct substitution gives an indeterminate form. In this case, multiply both the numerator and denominator by the conjugate of the numerator. For example, to evaluate the limit:
> limy→0(sec y − 1)/y^2
Multiply the numerator and denominator by the conjugate of the numerator, sec y + 1:
> limy→0((sec y − 1)(sec y + 1))/(y^2(sec y + 1))
This simplifies to:
> limy→0(tan^2y)/(y^2(sec y + 1))
Further simplifying gives:
> limy→0((sin y/y)^2/(cos^2 y)(sec y + 1))
Substituting y = 0 gives:
> limy→0(1^2/1/1/2) = 1/2
Usury Laws and Private Loans: What's the Verdict?
You may want to see also

Limit laws can be used to evaluate the limit of a function by using the squeeze theorem
In calculus, the squeeze theorem (also known as the sandwich theorem) is a method used to evaluate the limit of a function by "squeezing" or "sandwiching" it between two other functions whose limits are known. The theorem states that if a function g(x) is squeezed between f(x) and h(x) near a, and if f(x) and h(x) have the same limit L at a, then g(x) will also be forced to have the same limit L at a.
The squeeze theorem is particularly useful when the usual algebraic methods (such as factoring, conjugation, or other algebraic manipulations) are not effective in evaluating the limit of a function. It is often applied to oscillating functions that are considered discontinuous or undefined at the point of oscillation, allowing us to determine their limit values.
Let's consider the function g(x) = sin(x) and assume we want to find the limit as x approaches 0. We can use the squeeze theorem by setting:
F(x) = x, which is the lower bound of g(x) near x = 0
H(x) = 1, which is the upper bound of g(x) near x = 0
Since the limit of both f(x) and h(x) as x approaches 0 is 0, by the squeeze theorem, we can conclude that the limit of g(x) as x approaches 0 is also 0.
This example illustrates how the squeeze theorem helps us determine the limit of an oscillating function by "squeezing" it between two other functions with known limits.
In general, limit laws can be used to evaluate the limit of a function, but it is important to note that the existence of both individual limits is required for most of the laws. The squeeze theorem is a valuable tool within the set of limit laws, especially when dealing with oscillating functions or when standard algebraic methods are not sufficient.
Hunting Laws: Private Property Exemption or Exception?
You may want to see also
Frequently asked questions
Limit laws are a set of rules that allow us to find the limits of various combinations of functions.
No, limit laws can only be applied if both limits exist.
There are multiple types of limit laws, including the difference law, constant multiple law, product law, quotient law, power law, and root law.







