Demorgan's Law: Applicable To What?

De Morgan's Law, also known as De Morgan's Theorem, is a pair of transformation rules in Boolean algebra and set theory. The laws are named after 19th-century British mathematician Augustus De Morgan. The rules can be expressed in English as:

> The negation of A and B is the same as not A or not B.

> The negation of A or B is the same as not A and not B.

These laws can be applied to any number of statements. For example, the statement not A or not B or not C is equivalent to not (A and B and C).

Boolean algebra

De Morgan's laws, also known as De Morgan's theorems, are a pair of transformation rules that are valid rules of inference in propositional logic and Boolean algebra. Named after 19th-century British mathematician Augustus De Morgan, these laws express the relationship between the AND, OR, and NOT operations in Boolean algebra.

First De Morgan's Law

The first De Morgan's law states that the complement of the OR of two or more variables is equal to the AND of the complement of each variable.

Let A and B be two variables, then the first De Morgan's law is expressed as:

A + B)' = A' . B'

• + represents the OR operator
• represents the AND operator
• ' represents the complement operation

Second De Morgan's Law

The second De Morgan's law states that the complement of the AND of two or more variables is equal to the OR of the complement of each variable.

Let A and B be two variables, then the second De Morgan's law is expressed as:

A . B)' = A' + B'

• + represents the OR operator
• . represents the AND operator
• ' represents the complement operation

Applications in Boolean Algebra

De Morgan's laws are used in Boolean algebra to simplify and manipulate Boolean expressions, which are crucial in digital circuit design, computer science, and engineering. They allow us to convert between AND and OR gates by adding NOT gates, facilitating more efficient circuit layouts.

Examples

• NOT (A AND B) = (NOT A) OR (NOT B): This is an application of the first De Morgan's law, where we change the AND operation to an OR operation and add NOT operations to each variable.
• NOT (A OR B) = (NOT A) AND (NOT B): Similarly, this example uses the second De Morgan's law to change the OR operation to an AND operation and add NOT operations to each variable.
• NOT (A OR (NOT B)) = (NOT A) AND B: In this example, we first apply De Morgan's laws to the OR operation and then simplify the expression further.
• NOT (A AND NOT B) = (NOT A) OR B: Here, we apply De Morgan's laws to the AND operation and then simplify the expression.

Set theory

De Morgan's laws, also known as De Morgan's theorem, are a pair of transformation rules that are valid rules of inference. They are named after 19th-century British mathematician Augustus De Morgan. The laws apply to propositional logic, Boolean algebra, and set theory. In set theory, De Morgan's laws relate the intersection and union of sets through complements.

Type 1 De Morgan's Law

Type 1 De Morgan's law states that the complement of the union of any two sets, A and B, is equal to the intersection of their complements. This can be expressed as:

A U B)' = A' ∩ B'

This law can be visualised using Venn diagrams. The union of two sets, A and B, is the set of all elements that are either in set A or set B. The complement of the union, '>(A U B)', is the set of all elements that are not in A or B. This can be represented as the region outside of sets A and B in a Venn diagram.

The intersection of the complements, 'A' ∩ B', can also be visualised in a Venn diagram. A' is represented as the region outside of set A, and B' is the region outside of set B. The intersection of A' and B' is the region that is outside of both A and B.

By comparing the Venn diagrams for '>(A U B)' and 'A' ∩ B', we can see that they represent the same region. Therefore, we can conclude that (A U B)' = A' ∩ B', which is Type 1 of De Morgan's law.

Type 2 De Morgan's Law

Type 2 De Morgan's law is the opposite of Type 1. It states that the complement of the intersection of any two sets, A and B, is equal to the union of their complements. This can be expressed as:

A ∩ B)' = A' U B'

Using a similar approach to Type1, we can prove Type 2 of De Morgan's law using both mathematical and Venn diagram approaches.

Examples of De Morgan's Laws in Set Theory

Let's consider an example to illustrate the application of De Morgan's laws in set theory.

Let set U = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, set A = {2, 4, 6, 8}, and set B = {1, 3, 5, 7, 9}. We will prove both types of De Morgan's laws using these sets.

Proving Type 1 De Morgan's Law

Left-Hand Side:

The union of A and B is:

A U B = {2, 4, 6, 8} U {1, 3, 5, 7, 9} = {1, 2, 3, 4, 5, 6, 7, 8, 9}

The complement of the union is:

A U B)' = ({1, 2, 3, 4, 5, 6, 7, 8, 9})' = U - (A U B) = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10} - {1, 2, 3, 4, 5, 6, 7, 8, 9} = {0, 10}

Right-Hand Side:

First, let's find the complements of A and B:

A' = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10} - {2, 4, 6, 8} = {0, 1, 3, 5, 7, 9, 10}

B' = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10} - {1, 3, 5, 7, 9} = {0, 2, 4, 6, 8, 10}

Now, let's find the intersection of the complements:

A' ∩ B' = {0, 1, 3, 5, 7, 9, 10} ∩ {0, 2, 4, 6, 8, 10} = {0, 10}

Since the left-hand side and the right-hand side are equal, we have proven that (A U B)' = A' ∩ B', which is Type 1 of De Morgan's law.

Proving Type 2 De Morgan's Law

Left-Hand Side:

The intersection of A and B is:

A ∩ B = {2, 4, 6, 8} ∩ {1, 3, 5, 7, 9} = {Ⲫ}

The complement of the intersection is:

A ∩ B)' = U - (A ∩ B) = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10} - {Ⲫ} = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

Right-Hand Side:

First, let's find the complements of A and B:

A' = {0, 1, 3, 5, 7, 9, 10}

B' = {0, 2, 4, 6, 8, 10}

Now, let's find the union of the complements:

A' U B' = {0, 1, 3, 5, 7, 9, 10} U {0, 2, 4, 6, 8, 10} = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

Since the left-hand side and the right-hand side are equal, we have proven that (A ∩ B)' = A' U B', which is Type 2 of De Morgan's law.

Computer engineering

De Morgan's laws are widely used in computer engineering and digital logic to simplify circuit designs. They are a pair of transformation rules that are valid rules of inference in propositional logic and Boolean algebra. Named after 19th-century British mathematician Augustus De Morgan, the laws allow the expression of conjunctions and disjunctions in terms of each other via negation.

In computer engineering, De Morgan's laws can be applied to develop logic gates. They can also be used to simplify logical conditions in programming, without the need for strange symbols from Boolean algebra. De Morgan's laws can be particularly useful when there are more than two inputs, making truth tables more complex and time-consuming to draw out.

The laws are as follows:

• The negation of "A and B" is the same as "not A or not B."
• The negation of "A or B" is the same as "not A and not B."

In the context of computer engineering, these laws can be expressed as:

• NOT (A AND B) = (NOT A) OR (NOT B)
• NOT (A OR B) = (NOT A) AND (NOT B)

Using De Morgan's laws, we can convert one expression into another without changing the result. For example, the following expressions are equivalent:

• NOT(A) AND NOT(B) is the same as NOT(A OR B)
• NOT(A OR B) is the same as NOT(A) AND NOT(B)

De Morgan's laws can be used to find the equivalency of the NAND and NOR gates. They allow us to replace all the OR operators with AND operators or vice versa and then complement each of the terms or variables in the expression by inverting it (i.e., changing 0s to 1s and 1s to 0s).

In modern programming languages, the performance differences between these options may be negligible or non-existent due to the optimisation of compilers and interpreters. However, the application of De Morgan's laws can still improve the readability of larger logical expressions.

Text searching

De Morgan's laws are a pair of transformation rules that can be applied to text searching using Boolean operators AND, OR, and NOT.

Consider a set of documents containing the words "cats" and "dogs". De Morgan's laws state that the following two searches will return the same set of documents:

Search A: NOT (cats OR dogs)

Search B: (NOT cats) AND (NOT dogs)

The corpus of documents containing "cats" or "dogs" can be represented by four documents:

• Document 1: Contains only the word "cats".
• Document 2: Contains only "dogs".
• Document 3: Contains both "cats" and "dogs".
• Document 4: Contains neither "cats" nor "dogs".

To evaluate Search A, it is clear that the search "(cats OR dogs)" will return Documents 1, 2, and 3. So, the negation of that search (Search A) will return everything else, which is Document 4.

Evaluating Search B, the search "(NOT cats)" will return documents that do not contain "cats", which are Documents 2 and 4. Similarly, the search "(NOT dogs)" will return Documents 1 and 4. Applying the AND operator to these two searches (Search B) will return the documents that are common to these two searches, which is Document 4.

A similar evaluation can be applied to show that the following two searches will both return Documents 1, 2, and 4:

Search C: NOT (cats AND dogs)

Search D: (NOT cats) OR (NOT dogs)

De Morgan's laws are widely used in computer engineering and digital logic for simplifying circuit designs. They are also used in computer programming to simplify logical expressions in codes, thereby reducing the number of lines and optimising the code.

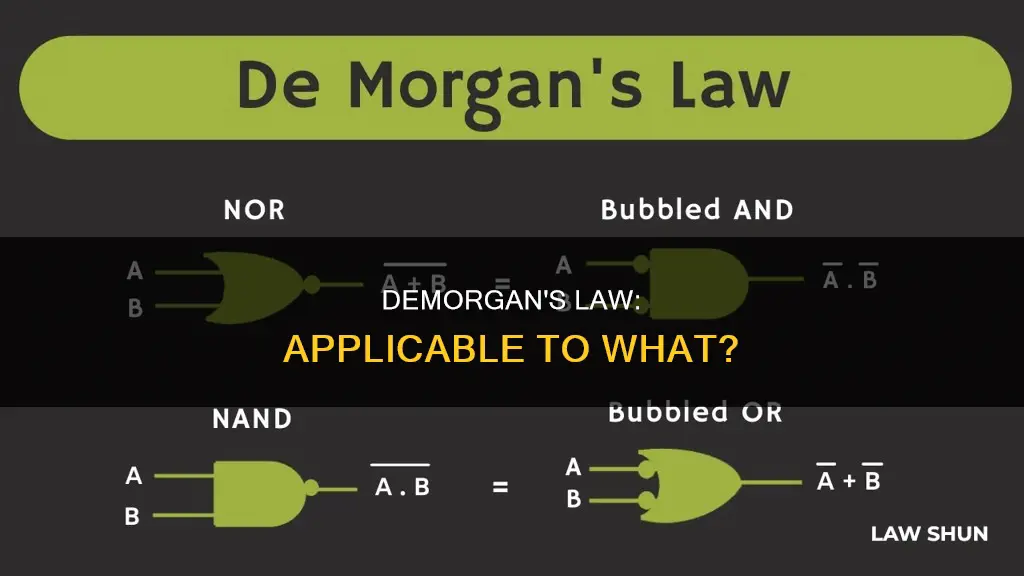
Circuit designs

De Morgan's laws, also known as De Morgan's theorem, are a set of rules that can be applied to circuit designs to simplify them. The laws are a pair of transformation rules that can be used to express conjunctions and disjunctions in terms of each other via negation.

In the context of circuit design, De Morgan's laws can be used to express the equivalence between gates with inverted inputs and gates with inverted outputs. This means that a NAND gate is equivalent to a Negative-OR gate, and a NOR gate is equivalent to a Negative-AND gate.

De Morgan's first theorem states that the complement of the product of two variables equals the sum of their complements. This can be expressed as:

> The complement of "A and B" is the same as "not A or not B."

De Morgan's second theorem states that the complement of the sum of two variables equals the product of their complements. This can be expressed as:

> The complement of "A or B" is the same as "not A and not B."

These theorems can be applied to circuit design to simplify complex Boolean logic expressions. For example, they can be used to convert AND gates into OR gates (and vice versa) using NOT gates, which can facilitate the creation of more efficient circuit layouts.

De Morgan's laws can also be used to express logic expressions not originally containing inversion terms in a different way, which can be useful when simplifying Boolean equations. However, when applying De Morgan's theorem in this way, care must be taken not to forget the final inversion. This can be avoided by complementing both sides of the expression before and after simplification.

Frequently asked questions