Does Hooke's Law Apply To Bending Objects?

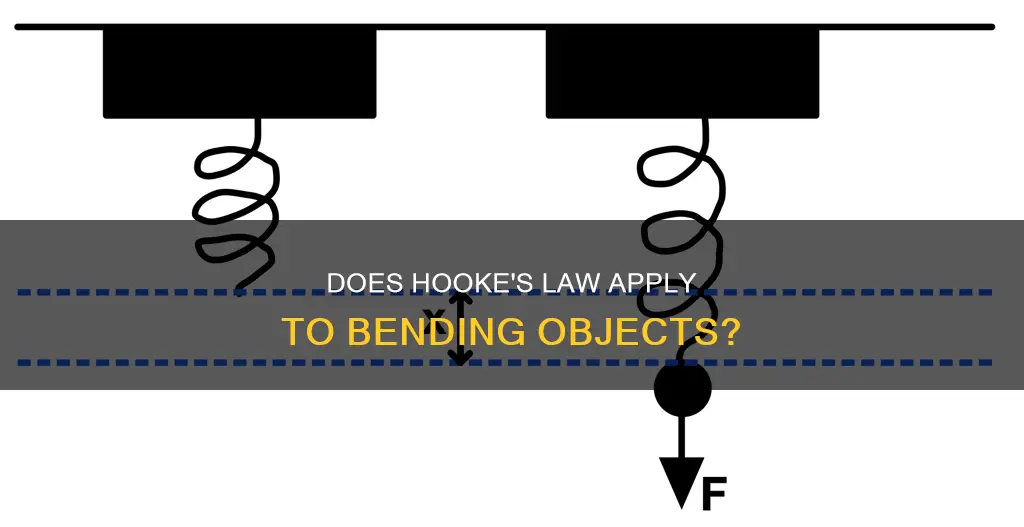
Hooke's Law is a fundamental principle of physics that describes the relationship between the force applied to an object and its subsequent displacement. It is named after 17th-century British physicist Robert Hooke, who discovered the law around 1660. The law states that the force required to extend or compress a spring is directly proportional to the distance of that extension or compression. This can be expressed mathematically as F = kx, where F is the force, x is the displacement, and k is the spring constant. Hooke's Law is not limited to springs, however, and can be applied to any elastic object, including objects being bent, as long as the deformation and stress can be expressed by a single number.

Hooke's Law and bending a flagpole

Hooke's Law is a principle of physics that states that the force required to extend or compress a spring by a certain distance is proportional to that distance. The law is named after 17th-century British physicist Robert Hooke, who aimed to demonstrate the relationship between the forces applied to a spring and its elasticity.

Hooke's Law can be applied to many loading situations, including the pure bending of beams. In this case, the outer fibres are subjected to tension, and the inner fibres are subjected to compression, resulting in the stretching or shortening of the fibres and beam deflection.

The law can be expressed mathematically as F = kx, where F is the force applied to the spring, x is the displacement of the spring, and k is the spring constant, which details the stiffness of the spring.

The law is not limited to springs, however, and can be applied to any elastic body that is deformed. For example, it can be used to understand the behaviour of a flagpole when bent. When a flagpole is bent, it experiences a deformation, and Hooke's Law can be used to understand the relationship between the force applied and the resulting displacement.

The value of k, or the spring constant, depends on the type of elastic material, as well as its dimensions and shape. Therefore, when applying Hooke's Law to a flagpole, one would need to consider the specific material, size, and shape of the flagpole to accurately calculate the force required to bend it and the resulting displacement.

It is important to note that Hooke's Law only applies within a limited frame of reference, as no material can be compressed or stretched beyond a certain point without permanent deformation. Therefore, it is most accurate when dealing with small amounts of force or deformation.

Hooke's Law and the extension spring

Hooke's Law is a fundamental principle of physics that describes the linear relationship between force and displacement. It is named after 17th-century British physicist Robert Hooke, who first stated the law in 1660 as a Latin anagram and published its solution in 1678 as "ut tensio, sic vis", which translates to "as the extension, so the force" or "the extension is proportional to the force".

Hooke's Law is expressed mathematically as F = -kX, where F is the force applied to an object, X is the displacement of the object, and k is the spring constant, which indicates the stiffness of the object. This law is particularly applicable to springs, including extension springs, and states that the force needed to extend or compress a spring is proportional to the distance of that extension or compression.

An extension spring is a type of spring that extends under load and returns to its original shape when the load is removed. These springs are usually made of metal and are coiled, with a variety of end types that allow for attachment to other components. When extended, the distance between the coils increases, and the spring gets longer.

Hooke's Law is essential for understanding the behaviour of extension springs. According to the law, the force required to extend an extension spring is directly proportional to the distance of that extension. This means that the spring will resist being stretched, and the amount of resistance increases as it is stretched further. The spring constant, k, for an extension spring depends on the material it is made of, as well as its dimensions and shape.

The behaviour of extension springs can be understood through Hooke's Law, which states that the force and displacement are linearly related. This means that the spring will return to its original shape after being extended, as long as the deformation is within the elastic limit. However, Hooke's Law only holds true for small deformations, and many materials will deviate from the law before reaching their elastic limits.

Hooke's Law and the torsion spring

Hooke's Law is a principle of physics that states that the force needed to extend or compress a spring is proportional to the distance it is extended or compressed. The law is named after 17th-century British physicist Robert Hooke, who first stated the law in 1660 as a Latin anagram and then published the solution in 1678 as "ut tensio, sic vis", which translates to "as the extension, so the force" or "the extension is proportional to the force".

Hooke's Law is the principle of physics behind the elasticity, torsion, and force involved with springs. It states that the extension of a spring is proportional to the load that is applied to it, as long as the load does not exceed the material's elastic limit. This can be expressed mathematically as F = kx, where F is the force applied to the spring, k is the spring constant, and x is the displacement of the spring.

Torsion springs, which are essential components in numerous mechanical applications, operate under the principles of Hooke's Law. Hooke's Law states that the torque in a torsion spring is proportional to the angle of torsion. This fundamental relationship, expressed as T = kθ, where T is the torque and θ is the angle of torsion, is essential for the design and analysis of these springs.

The design of torsion springs involves a deep understanding of the torsion constant and material properties. Engineers must consider factors such as shear strength, elastic limits, and environmental conditions in which the spring will operate. The use of advanced tools such as the Online Spring Force Tester and Spring Creator 5.0 can aid in the design and analysis of torsion springs.

Hooke's Law and the compression spring

Hooke's Law is a fundamental principle of physics that describes the relationship between the force required to extend or compress a spring and the distance it is extended or compressed. It is named after 17th-century British physicist Robert Hooke, who first stated the law in 1660 as a Latin anagram and published the solution in 1678 as "ut tensio, sic vis", which translates to "as the extension, so the force" or "the extension is proportional to the force".

The law can be expressed mathematically as F = -kX, where F is the force applied to the spring, X is the displacement of the spring, and k is the spring constant, which indicates the stiffness of the spring. This equation holds true for a variety of spring types, including compression springs, extension springs, and torsion springs.

Hooke's Law is a key concept in understanding the behaviour of springs and other elastic objects. It states that the force required to extend or compress a spring is directly proportional to the distance it is extended or compressed. This means that the more a spring is stretched or compressed, the greater the force required to stretch or compress it further.

The law also applies to other situations where an elastic body is deformed, such as when a force is applied to a rubber band or a balloon is inflated. In the context of compression springs, Hooke's Law describes the relationship between the force applied to the spring and the resulting change in length. The spring will return to its original shape after the load is removed, as long as the load does not exceed the material's elastic limit.

Hooke's Law is a foundational principle in several branches of science and engineering, including seismology, molecular mechanics, and acoustics. It also plays a crucial role in the design and function of various devices and technologies, such as mechanical clocks, spring scales, and manometers.

Hooke's Law and the coil spring

Hooke's Law is a fundamental principle of physics that describes the relationship between force and displacement. It is named after 17th-century British physicist Robert Hooke, who formulated it in 1660 and published the solution in 1678. Hooke's Law is expressed by the equation F = kx, where F is the force applied to an object, x is the displacement of the object, and k is a constant representing the stiffness of the object.

Hooke's Law specifically applies to elastic objects, which can return to their original shape after experiencing distortion. This ability is known as a "restoring force", and it is proportional to the amount of stretch or deformation experienced by the object. In the context of springs, this means that the extension of a spring is directly proportional to the load applied to it, as long as the load does not exceed the material's elastic limit.

Coil springs are a type of spring that was directly influenced by Hooke's Law. They are used in a wide range of applications, including automotive suspension systems, playground toys, furniture, and retractable ballpoint pens. The understanding of Hooke's Law allows engineers to predict the behaviour of coil springs when force is applied and design them for specific applications.

In addition to its applications in spring systems, Hooke's Law also has broader implications. It can be applied to any situation where an elastic body is deformed, such as inflating a balloon, pulling on a rubber band, or analysing the stress on a bending beam. Furthermore, it is compatible with Newton's laws of static equilibrium, allowing for the deduction of the relationship between strain and stress for complex objects.

Frequently asked questions