Kepler's laws of planetary motion describe the orbits of planets around the Sun. However, they can also be applied to moons. Kepler's first law implies that the Moon's orbit is an ellipse with the Earth at one focus. The Moon's orbit is nearly elliptical, with an eccentricity of 0.055. The Moon's orbit can be more accurately described as elliptical with perturbations, as the Sun and the fact that the Earth is not a perfect sphere cause the most significant perturbations. Kepler's third law can be used to calculate the semimajor axis of the Moon's orbit.
| Characteristics | Values |
|---|---|
| Does Kepler's Third Law apply to moons? | Yes |
| Kepler's Third Law | The square of a planet's orbital period is proportional to the cube of the length of the semi-major axis of its orbit |
| The orbit of the moon | Elliptical with an eccentricity of 0.055 |
| Kepler's First Law | The orbit of a planet is an ellipse with the Sun at one of the two foci |
| Kepler's Second Law | A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time |
| Kepler's Third Law | The square of a planet's orbital period is proportional to the cube of the length of the semi-major axis of its orbit |
| Kepler's laws | Apply whenever one body gravitationally dominates the others |
| Kepler's Third Law in relation to the moon | The Moon's orbital period is approximately 27 days, and the semi-major axis of the Moon's orbit is 3.8 x 10^8 m |
What You'll Learn

Kepler's third law applies to the Moon's orbit around Earth
Kepler's three laws of planetary motion describe the orbits of planets around the Sun. However, with minor modifications, they can also be applied to the Moon's orbit around the Earth.
Kepler's first law states that the orbit of a planet is an ellipse with the Sun at one of the two foci. The Moon's orbit is also elliptical, but with the Earth at one focus. This is reflected in the variation of the Moon's distance from the Earth, which changes by about 13% as the Moon travels in its orbit.
The second law states that a line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time. This law explains how planetary velocities vary, with planets travelling faster when they are closer to the Sun. Similarly, when the Moon is closest to the Earth (perigee), it moves faster, and when it is furthest from the Earth (apogee), it moves slower.
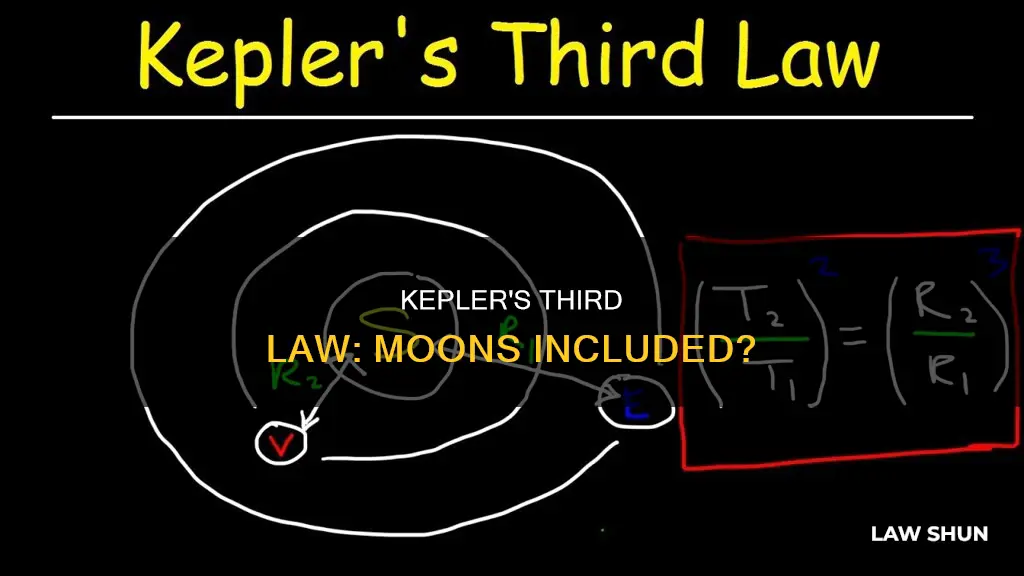
The third law, also known as the harmonic law, states that the square of a planet's orbital period is proportional to the cube of the length of the semi-major axis of its orbit. This law establishes a relationship between the distance of planets from the Sun and their orbital periods.
Kepler's third law can be applied to the Moon's orbit around the Earth. The Moon completes one orbit around the Earth approximately every 27 days, with a semi-major axis of approximately 3.8 x 10^8 meters. By substituting the values of the Moon's orbital period and Kepler's constant into the mathematical expression of the third law, we can calculate the semi-major axis of the Moon's orbit.
In summary, Kepler's third law can be applied to the Moon's orbit around the Earth, with the necessary modifications to account for the different celestial bodies involved. This application of the law helps us understand the characteristics of the Moon's orbit, such as its shape, the variation in the Moon's speed, and the relationship between its orbital period and the length of the semi-major axis.
HIPAA Laws: Do They Apply to Veterinary Practices?
You may want to see also

The Moon's orbit is elliptical
Kepler's laws of planetary motion describe how planetary bodies orbit the Sun. Kepler's first law states that the orbit of every planet is an ellipse with the Sun at one of the two foci. This means that the Sun is located at one focus of the elliptical orbit, and the planet follows the ellipse in its orbit, resulting in a constant change in the distance between the planet and the Sun as the planet moves.
The Moon's orbit is indeed elliptical, with the Earth at one focus. The distance from the Earth to the Moon varies by about 13% as the Moon travels in its orbit. This variation can be observed through the Moon's apparent diameter: when the Moon is closest to Earth (perigee), it appears larger, and when it is furthest from Earth (apogee), it looks smaller.
The elliptical shape of the Moon's orbit can be explained by Newton's theory of gravity, which states that if there are two particles in orbit around each other, they will have an elliptical orbit. However, if there are more than two bodies, the gravity of other bodies will cause perturbations, affecting the orbit. In the case of the Moon, the most significant perturbations come from the Sun and the fact that the Earth is not a perfect sphere. Other planets and tides also have minor effects on the Moon's elliptical orbit.
Therefore, while the Moon's orbit is primarily elliptical, it can be more accurately described as "Elliptical + perturbations."
Thermodynamics and DND: A Lawful Game?
You may want to see also

The Sun is not at the centre of the Moon's orbit
Kepler's laws of planetary motion describe the orbits of planets around the Sun. The laws state that the orbit of a planet is an ellipse with the Sun at one of the two foci. However, it is important to note that these laws do not necessarily place the Sun at the centre of the orbit. In fact, according to Kepler's first law, the Sun is not at the centre but at a focal point of the elliptical orbit.
This concept can be applied to the motion of the Moon around the Earth. The Moon's orbit is not a perfect circle but is instead a nearly circular ellipse with an eccentricity of around 0.0549. This means that the Moon's orbit has a slight oval shape, and the Earth is located at one of the foci of this elliptical path. As a result, the distance between the Moon and the Earth varies, and the Moon appears larger or smaller in the sky depending on its position in its orbit.
The Moon's orbit is influenced not only by the Earth's gravity but also by the gravitational pull of the Sun and other planets. These gravitational interactions cause perturbations in the Moon's orbit, resulting in variations in its distance from the Earth and its orbital speed. Additionally, the Moon's orbit is inclined by about 5.1 degrees with respect to the ecliptic plane, while the Earth's equatorial plane is tilted by about 23 degrees relative to the same plane.
The Moon's orbit has been a subject of study for centuries, with ancient civilisations such as the Babylonians keeping detailed records of lunar observations. The elliptical nature of the Moon's orbit and its impact on the appearance and behaviour of the Moon continue to be areas of exploration and research in astronomy.
Antique Firearms: Concealed Carry Law Exemptions?
You may want to see also

The Moon's distance from Earth varies by about 13%
The Moon's orbit around the Earth is elliptical, with the Earth at one focus. This means that the Moon's distance from the Earth varies as it travels in its orbit. Specifically, the distance between the Moon and the Earth changes by about 13% as the Moon moves through its orbit, from a minimum distance of 226,000 miles (363,300 km) to a maximum of 251,000 miles (405,500 km). This variation can be observed through the Moon's changing apparent diameter and speed. When the Moon is closest to the Earth (perigee), it appears larger and moves faster, while when it is furthest away (apogee), it appears smaller and moves slower.
The Moon's elliptical orbit can be explained by Kepler's laws of planetary motion, specifically the first law, which states that a planet travels around the Sun in an elliptical orbit with the Sun at one focus. This law can be applied to the Moon's orbit around the Earth by substituting the Earth for the Sun and the Moon for the planet. Therefore, the Moon's orbit can be described as an ellipse with the Earth at one focus.
The variation in the Moon's distance from the Earth has several effects. One notable effect is the change in the Moon's apparent diameter. When the Moon is closer to the Earth, it appears larger, and when it is farther away, it appears smaller. This change in apparent diameter can be observed and measured using a telescope. Another effect of the varying distance is the Moon's changing speed. Due to tidal forces, when the Moon is at perigee, it moves faster, while at apogee, it moves slower. This variation in speed influences the timing of ocean tides on Earth.
The Moon's orbit is not a perfect ellipse due to perturbations caused by the gravitational influence of other celestial bodies, such as the Sun and other planets. These perturbations cause the Moon's orbit to deviate slightly from a perfect elliptical path. However, despite these perturbations, Kepler's laws still provide a useful description of the Moon's motion around the Earth, with minor modifications.
Road Rules and Car Parks: Where Do Laws Apply?
You may want to see also

The Moon's orbit can be calculated using the Kepler constant
Kepler's laws of planetary motion describe the orbits of planets around the Sun. These laws were published by Johannes Kepler in 1609, without the third law, and in full in 1619. Kepler's first law implies that the Moon's orbit is an ellipse with the Earth at one focus. The distance from the Earth to the Moon varies by about 13% as the Moon travels in its orbit. Kepler's three laws, designed to describe the orbital motion of planets about the Sun, can also be used to describe the Moon's motion about the Earth, the orbits of Jupiter's satellites, and even the orbital motions of binary stars.
Kepler's third law can be used to calculate the Moon's orbit. The Moon completes one orbit around the Earth approximately every 27 days, so its orbital period T is approximately 27 days. The Kepler constant K for a body orbiting Earth is 9.91·10-14 s2/m3, or, 1.33·10-23 days2/m3. Using this information and Kepler's third law, we can determine the semi-major axis of the Moon's orbit.
Kepler's third law can be expressed mathematically as:
> The square of a planet's orbital period is proportional to the cube of the length of the semi-major axis of its orbit.
We know the period of the Moon's orbit T and Kepler's constant K. To calculate the semi-major axis a of the Moon's orbit, we isolate 'a' by dividing both sides of the previous equation by K. We then take the cubic root of both sides of the equation, and substitute the values of T and K in their correct units to find the value of 'a'.
Therefore, the semi-major axis of the Moon's orbit is:
> a= ((27 days)2 /(1.33·10-23 days2/m3))1/ 3= 3.8 · 108 m.
So, the Moon's orbit can be calculated using the Kepler constant.
Idling Laws: Do They Apply to Semi Trucks?
You may want to see also
Frequently asked questions
Yes, Kepler's third law applies to moons. Kepler's third law states that the square of a planet's orbital period is proportional to the cube of the length of the semi-major axis of its orbit. This law applies to moons as well, as they also have orbital periods and semi-major axes that can be used to calculate their orbits.
Kepler's third law states that the square of a planet's orbital period is proportional to the cube of the length of the semi-major axis of its orbit. In other words, the ratio of the square of an object's orbital period to the cube of the semi-major axis of its orbit is the same for all objects orbiting the same primary body.
To calculate the semi-major axis of a moon's orbit using Kepler's third law, you need to know the moon's orbital period and the Kepler constant for a body orbiting the planet that the moon is orbiting. You can then use Kepler's third law equation and substitute the values in the correct units to find the value of the semi-major axis.







