Kirchhoff's Voltage Law (KVL) is a principle in electronics that states: The algebraic sum of all voltages in a loop must equal zero. In other words, the total voltage around a closed-loop network is equal to the sum of all the voltage drops within the same loop. KVL applies to any circuit configuration, including series and parallel circuits. By using KVL, we can solve complex circuit problems and determine unknown voltages and currents within a circuit.
| Characteristics | Values |
|---|---|
| Name | Kirchhoff's Voltage Law (KVL) |
| Discovered by | Gustav R. Kirchhoff, a German physicist |
| Year discovered | 1845 or 1847 |
| Application | Applicable to all circuits, including parallel circuits |
| Formula | The algebraic sum of all voltages in a loop must equal zero |
| Loop | Any path traced from one point in a circuit around to other points and finally back to the initial point |
| Polarity | Accounting for signs (polarities) as well as magnitudes |
| Use case | Determining unknown voltage in a complex circuit |
What You'll Learn
- Kirchhoff's Voltage Law (KVL) states that the sum of all voltage sources and drops in a closed loop is equal to zero
- KVL can be used to determine an unknown voltage in a complex circuit
- KVL can be applied to any circuit configuration, not just simple series
- KVL can be used to analyse series circuits
- KVL is based on the principle of conservation of energy

Kirchhoff's Voltage Law (KVL) states that the sum of all voltage sources and drops in a closed loop is equal to zero
Kirchhoff's Voltage Law (KVL) was developed by German physicist Gustav Kirchhoff in 1845 or 1847. KVL states that the sum of all voltage sources and drops in a closed loop is equal to zero. In other words, the algebraic sum of all the voltages in a closed loop network must equal zero.
The law can be applied to any closed-loop network driven by a voltage source. It is important to note that the direction of the loop does not matter; the voltage sum will still equal zero. KVL can be used to determine unknown voltages in a complex circuit.
> Three resistors are connected across a 50-volt source. What is the voltage across the third resistor if the voltage drops across the first two resistors are 25 volts and 15 volts?
To solve this problem, we first assume a direction of current flow and assign polarities to the voltages. Starting at point A, we trace around the circuit in the direction of the current flow, recording the voltage and polarity of each component. Substituting the values from the circuit into the KVL equation, we find that the unknown voltage is 10 V.
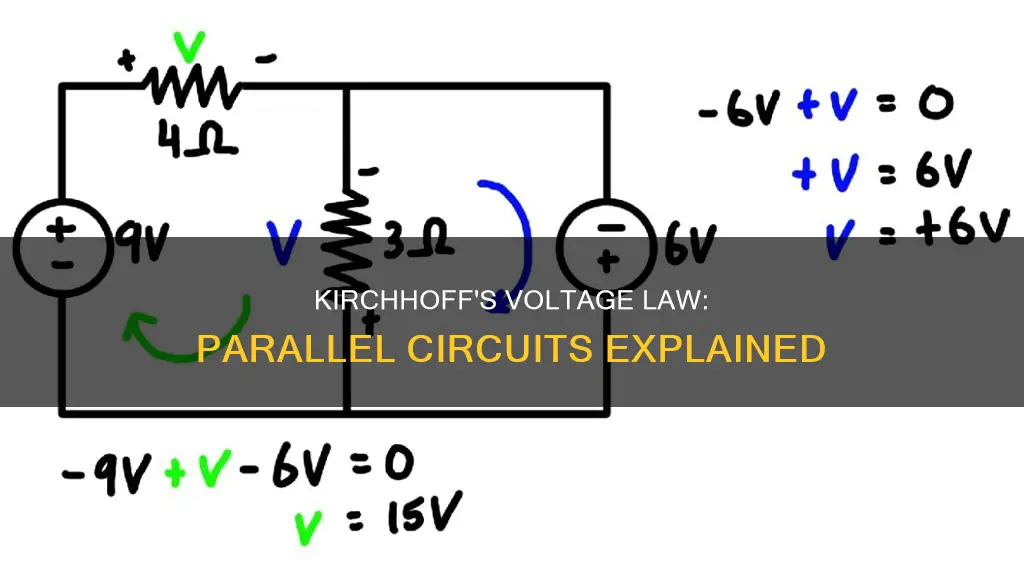
KVL can be applied to any circuit configuration, including series and parallel circuits. In a series circuit, the same current flows through all the components, and the sum of the voltage drops across each load is equal to the voltage of the source. In a parallel circuit, there is more than one path for the current to flow through, and the voltage across every resistor is the same as the supply voltage.
By applying KVL to a parallel circuit, we can derive the rule that the potential differences in a parallel circuit are all equal. This means that the sum of the voltage drops across all the components in a parallel circuit is equal to the supply voltage.
The Law's Equality: Does It Exist?
You may want to see also

KVL can be used to determine an unknown voltage in a complex circuit
Kirchhoff's Voltage Law (KVL) can be used to determine an unknown voltage in a complex circuit. KVL states that the sum of the voltages in a closed loop will equal zero. In other words, if you look at any loop that goes all the way around, any increases in voltage throughout the loop will be offset by an equal amount of decreases in voltage.
To use KVL to find an unknown voltage, follow these steps:
- Identify the loop that contains the unknown voltage.
- Assign a current direction to the loop.
- Write down the KVL equation for the loop, including the unknown voltage.
- Measure the voltages around the loop using a voltmeter, noting the polarities.
- Substitute the measured voltages into the KVL equation.
- Solve the equation to find the value of the unknown voltage.
For example, consider a complex circuit with two series circuits joined by a single wire. To determine the voltage between points 3 and 4, we can set up a KVL equation with the voltage between those points as the unknown. Stepping around the loop 3-4-9-8-3, we measure the voltages as follows:
- Voltage from point 9 to point 4: +12V
- Voltage from point 3 to point 8: +20V
- Voltage from point 8 to point 9: 0V
Using KVL, we can write the equation as V_4-3 = V_9-4 + V_3-8 + V_8-9. Substituting the measured voltages, we get V_4-3 = +12V + +20V + 0V. Therefore, the final answer for the voltage from point 4 to point 3 is -32V.
It is important to note that the placement of the voltmeter leads can affect the polarity of the measured voltage. In the above example, if we had started the loop at point 3 and ended at point 4, we would have obtained the same magnitude of voltage (32V) but with a positive polarity, indicating that point 4 is positive with respect to point 3.
Foreign Laws in Embassies: Whose Rules Apply?
You may want to see also

KVL can be applied to any circuit configuration, not just simple series
Kirchhoff's Voltage Law (KVL) applies to any circuit configuration, not just simple series. It is a powerful tool for solving complex circuit problems and understanding voltage distribution. KVL states that the algebraic sum of all voltages in a closed loop within a circuit is equal to zero. This means that the sum of the voltage drops across all components in a closed loop will always be zero, regardless of whether they are in series or parallel.
The versatility of KVL is evident in its ability to analyse circuits with various configurations, including parallel circuits. In a parallel circuit, the voltage across each resistor is the same as the supply voltage. For example, in a simple parallel circuit with a supply voltage of 6 volts, the voltage across each resistor will also be 6 volts. Applying KVL, the sum of these voltages around the loop will equal the supply voltage, resulting in a sum of zero. This demonstrates that KVL holds true for parallel circuits.
Furthermore, KVL can be applied to complex circuits with multiple branches and loops. By following the principles of KVL, we can analyse each closed loop within the circuit, considering the direction of current flow and the polarities of the voltage drops. This allows us to set up equations and calculate unknown voltages or currents within the circuit.
The applicability of KVL to any circuit configuration stems from its foundation in the conservation of energy. Voltage represents the energy per unit charge, and as charges move within a circuit, the energy changes. KVL ensures that the total energy change around any closed loop is zero, aligning with the principle of energy conservation.
It is important to note that while KVL applies to all circuit configurations, the specific techniques for applying it may vary. For instance, in a series circuit, the same current flows through each component, resulting in a straightforward application of KVL. In contrast, parallel circuits have multiple paths for current flow, requiring careful consideration of the different branches and their connections.
In summary, Kirchhoff's Voltage Law is a versatile tool that can be applied to any circuit configuration. Its applicability extends beyond simple series circuits and includes parallel circuits, complex circuits, and even "black box" circuits. By following the principles of KVL and considering voltage drops and polarities, we can analyse and solve problems for a wide range of circuit setups.
CAS and Law School Applications: Are They Necessary?
You may want to see also

KVL can be used to analyse series circuits
Kirchhoff's Voltage Law (KVL) is a fundamental principle in electrical circuits that states: "The algebraic sum of all voltages in a loop must equal zero." This law, discovered by German physicist Gustav Kirchhoff in 1847, is applicable to any closed-loop series path in a circuit.
- Understand Voltage Polarity: Recognise that voltage polarity is crucial in KVL. It refers to the signs (+ and -) of the sources and voltage drops across components in the circuit.
- Assign Current Direction: Assume a direction for the current flowing through the circuit. While the correct direction is desirable, it is not necessary.
- Assign Voltage Polarities: Using the assumed current direction, assign positive and negative polarities to the voltages across each resistor or component. The positive end is where the current flows into the resistor, and the negative end is where it leaves.
- Trace the Circuit Loop: Starting at any point, trace the circuit in a chosen direction (clockwise or counterclockwise). Write down the voltage and polarity of each component as you go.
- Apply KVL Equation: Place the voltages and their polarities into the KVL equation: ΣV = 0, where V1, V2, etc. are the voltages in the loop.
- Solve for Unknowns: Solve the equation to find unknown voltage values or currents in the circuit.
For example, consider a series circuit with three resistors, R1, R2, and R3, connected across a voltage source. If the voltage drops across R1 and R2 are known, you can use KVL to find the voltage drop across R3. Assign a current direction, trace the loop, and apply KVL: V1 + V2 + V3 = 0, where V3 is the unknown voltage drop.
KVL is a powerful tool for analysing series circuits, allowing for the calculation of unknown voltages and currents. It provides a method to determine the distribution of voltages in complex series circuits, making it a valuable technique in electrical engineering.
HIPAA Laws: Do They Apply to Dentists?
You may want to see also

KVL is based on the principle of conservation of energy
Kirchhoff's Voltage Law (KVL) is based on the principle of conservation of energy. Gustav Kirchhoff's second law states that the algebraic sum of all the voltage drops in a closed loop is equal to zero. This is because a circuit loop is a closed conducting path, so no energy is lost.
In other words, the algebraic sum of all the potential differences around the loop must be equal to zero. This means that the polarities and signs of the sources and voltage drops around the loop must be taken into account.
Kirchhoff's Voltage Law can be applied to any circuit configuration, including series and parallel circuits. When applying KVL to a specific circuit element, it is important to pay attention to the algebraic signs of the voltage drops across elements and the emf's of sources, otherwise, calculations may be incorrect.
The direction of current flow around a closed circuit can be assumed to be either clockwise or anticlockwise, and the result will still be correct and valid. However, if the chosen direction is different from the actual direction of current flow, the algebraic answer will have a minus sign.
Kirchhoff's Voltage Law is a useful tool for circuit analysis, particularly when dealing with series circuits, as they also act as voltage dividers.
Understanding Minimum Wage Laws for Minors
You may want to see also
Frequently asked questions
Kirchhoff's Voltage Law (KVL) states that the algebraic sum of the voltages in any closed path or loop in a circuit is equal to zero. In other words, the total voltage around a closed loop is equal to the sum of all the voltage drops within the same loop.
Yes, Kirchhoff's Voltage Law can be applied to any circuit configuration, including parallel circuits. It is a fundamental principle that holds true regardless of the circuit topology.
Some key terms include circuit, path, node, branch, loop, and mesh. A circuit is a closed loop conducting path with electric current flowing through it. A node is a junction or connection point within a circuit where two or more elements are joined. A branch is a single or group of components connected between two nodes. A loop is a simple closed path in a circuit without any intersecting paths.
Kirchhoff's Voltage Law allows us to solve complex circuit problems by defining a set of basic network laws and theorems for voltages and currents. It enables us to determine unknown voltages or currents in a circuit by setting up equations for closed loops.
Kirchhoff's Voltage Law assumes that all voltages and resistances in the circuit are known or can be measured. It also requires a proper understanding of voltage polarity and its application in the circuit.







