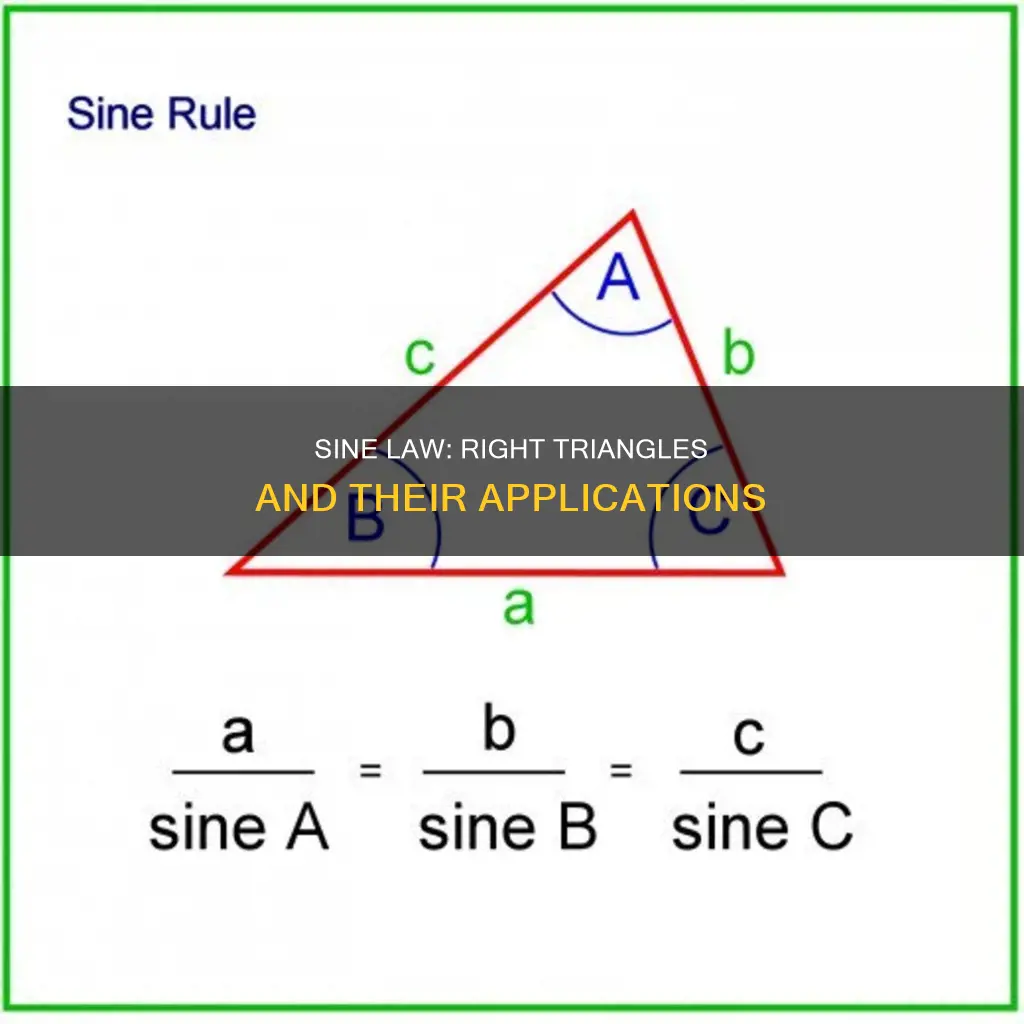
The Law of Sines, also known as the Sine Rule, is a formula used to find unknown sides or angles in triangles. The formula is represented by the equation:
> (sin A / a) = (sin B / b) = (sin C / c)
Where a, b, and c are the sides of a triangle, and A, B, and C are the angles. The law of sines is typically used for non-right triangles, also known as oblique triangles. However, it can also be applied to right triangles. In a right triangle, the hypotenuse is the side opposite the right angle, and the remaining sides are the legs. The law of sines can be used to find unknown sides or angles in right triangles by setting up and solving equations based on the known values.
| Characteristics | Values |
|---|---|
| Does the law of sines apply to right triangles? | Yes, the laws apply to right triangles. |
| What is the law of sines? | The law of sines is one of the most useful triangle equations in mathematics. It allows us to make calculations based on the angles of triangles rather than their sides. |
| What is the law of sines also known as? | The law of sines is also known as the Sine Rule, Sine Law or Sine Formula. |
| What is the equation for the law of sines? | a/Sin A = b/Sin B = c/Sin C |
| What does the law of sines do? | The law of sines is used to find the unknown angle or the side of an oblique triangle. |
| What is an oblique triangle? | Any triangle that is not a right triangle. |
| When can the law of sines be used? | The law of sines can be used when we know two angles and one side or two angles and one included side. |
| What is the sine rule? | The ratio of the side length of a triangle to the sine of the opposite angle. |
What You'll Learn
- The Law of Sines is used to find the unknown angle of an oblique triangle
- The law is also known as the Sine Rule, Sine Law or Sine Formula
- The law of sines can be used to find the unknown side of a triangle
- The law of sines can be used when we know two angles and one side or two angles and one included side
- The sine rule formula can be represented as: a/Sin A = b/Sin B = c/Sin C

The Law of Sines is used to find the unknown angle of an oblique triangle
The Law of Sines, also known as the Sine Rule, is a formula used to find the unknown angle or side of an oblique triangle. An oblique triangle is any triangle that is not a right triangle.
The Law of Sines is represented by the following equation:
> a/sin A = b/sin B = c/sin C
In this equation, a, b, and c are the sides of a triangle, and A, B, and C are the angles. The hypotenuse of a right triangle is also considered the side opposite the 90-degree angle.
The Law of Sines is based on proportions and can be presented in two ways:
> sin A/a = sin B/b = sin C/c
> a/sin A = b/sin B = c/sin C
The Law of Sines can be used to solve oblique triangles without first dividing them into right triangles. There are three possible cases: ASA, AAS, and SSA. In the ASA case, we know the measurements of two angles and the included side. In the AAS case, we know the measurements of two angles and a side that is not between them. In the SSA case, we know the measurements of two sides and an angle that is not between them.
The Law of Sines can also be used to find the unknown angle of an oblique triangle. For example, if we know the value of one side and the values of two angles, we can use the formula to find the unknown angle.
> sin A/a = sin B/b = sin C/c
Let's say we know the following:
> a = 7 cm, angle A = 60 degrees, angle B = 45 degrees
We can plug these values into the formula:
> 7/sin 60 degrees = b/sin 45 degrees
> 7/(sqrt(3)/2) = b/(1/sqrt(2))
> b = 14/(sqrt(6)
So, the length of side b is approximately 14/sqrt(6).
The Law of Sines is a useful tool for solving oblique triangles and finding unknown angles and sides. It is based on the relationship between the angles and sides of a triangle and can be applied in various real-world scenarios, such as engineering and astronomy.
Hunting Laws: Private Property Exemption or Exception?
You may want to see also

The law is also known as the Sine Rule, Sine Law or Sine Formula
The law of sines is also known as the Sine Rule, Sine Law, or Sine Formula. It is one of the most useful triangle equations in mathematics. The law of sines relates the lengths of the sides of any triangle to the sines of its angles.
The law of sines is defined as the ratio of side length to the sine of the opposite angle. This ratio is equivalent for all three sides of a triangle with respect to their sides and angles. The law of sines formula is:
$$\\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}$$
Where a, b, and c are the lengths of the sides of a triangle, and A, B, and C are the opposite angles.
The law of sines can be used to compute the remaining sides of a triangle when two angles and one side are known, or when two sides and one non-enclosed angle are known. It can also be used to find unknown angles or sides of a triangle, especially non-right triangles or oblique triangles.
The sine rule can be represented in three different ways:
- $$\\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}$$
- $$\\frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c}$$
- $$\\frac{a}{b} = \frac{\sin A}{\sin B}; \frac{a}{c} = \frac{\sin A}{\sin C}; \frac{b}{c} = \frac{\sin B}{\sin C}$$
The law of sines is not just useful in mathematics. It is also applied in real life, such as in engineering to measure the angle of tilt, in astronomy to measure distances between planets or stars, and in navigation.
HIPAA Laws and Spouses: What You Need to Know
You may want to see also

The law of sines can be used to find the unknown side of a triangle
The law of sines, also known as the sine rule, is a formula that defines the ratio of the sides of a triangle to the sine of the opposite angle. The formula is represented as:
> a/sin A = b/sin B = c/sin C
Where a, b, and c are the sides of a triangle, and A, B, and C are the angles. This formula can be used to find the unknown side of a triangle when two angles and one side, or two sides and a non-included angle, are known.
To find the unknown side, follow these steps:
- Substitute the known values into the formula.
- Remove any fractions that are unhelpful.
- Solve the remaining equation.
For example, let's say we have a triangle with the following properties:
> a = 8 cm, B = 45°, C = 60°
We can use the law of sines to find the length of side b:
> a/sin A = b/sin B = c/sin C
> 8/sin 60° = b/sin 45°
> b = (8 × sin 45°) / sin 60°
> b = 8 × (√2/2) / (√3/2)
> b = 8/√6
> b = 4.899 cm
So, the length of side b is approximately 4.9 cm.
The law of sines is a versatile tool that can be applied to any triangle, including right triangles. It allows us to make calculations based on the angles of triangles rather than their sides, providing a powerful method for solving unknown values in trigonometry.
Employment Discrimination Law: Resident Aliens' Rights Explored
You may want to see also

The law of sines can be used when we know two angles and one side or two angles and one included side
The law of sines can be used to solve oblique triangles, which are triangles that are not right triangles. It defines the ratio of the sides of a triangle to their respective sine angles.
The law of sines can be used when we know two angles and one side, or two angles and one included side. This is known as the ASA (Angle-Side-Angle) or AAS (Angle-Angle-Side) criteria.
Let's say we have triangle ABC, with angle A = 20°, angle B = 60°, and side a = 10. We can use the law of sines formula to solve for side b:
\[\frac{\sin A}{a} = \frac{\sin B}{b}\]
\[\frac{\sin 20°}{10} = \frac{\sin 60°}{b}\]
\[b = \frac{10 \sin 60°}{\sin 20°}\]
Now, we can find angle C by subtracting angles A and B from 180° (the sum of the angles in a triangle):
\[C = 180° - 20° - 60° = 100°\]
Finally, we can use the law of sines again to find side c, using angle A and side a since their exact values are known:
\[\frac{\sin A}{a} = \frac{\sin C}{c}\]
\[\frac{\sin 20°}{10} = \frac{\sin 100°}{c}\]
\[c = \frac{10 \sin 100°}{\sin 20°}\]
So, the solutions for triangle ABC are: angle A = 20°, angle B = 60°, angle C = 100°, side a = 10, side b = 14/√6, and side c = 10/√3.
Let's consider triangle LMN, with angle L = 30°, angle M = 40°, and side n = 12. First, we need to find angle N using the fact that the sum of the angles in a triangle is 180°:
\[N = 180° - L - M = 180° - 30° - 40° = 110°\]
Now, we can use the law of sines to find side ℓ:
\[\frac{\sin N}{n} = \frac{\sin L}{ℓ}\]
\[\frac{\sin 110°}{12} = \frac{\sin 30°}{ℓ}\]
\[ℓ = \frac{12 \sin 30°}{\sin 110°}\]
Next, we can use the law of sines again to find side m, using angle N and side n:
\[\frac{\sin N}{n} = \frac{\sin M}{m}\]
\[\frac{\sin 110°}{12} = \frac{\sin 40°}{m}\]
\[m = \frac{12 \sin 40°}{\sin 110°}\]
So, the solutions for triangle LMN are: angle L = 30°, angle M = 40°, angle N = 110°, side ℓ = 12/√3, side m = 12/√6, and side n = 12.
Traffic Laws in Parking Lots: What You Need to Know
You may want to see also

The sine rule formula can be represented as: a/Sin A = b/Sin B = c/Sin C
The Law of Sines, also known as the Sine Rule, is a formula used to find the unknown angle or side of a triangle. The formula is represented as:
A/Sin A = b/Sin B = c/Sin C
Here, 'a', 'b' and 'c' represent the sides of a triangle, while 'A', 'B' and 'C' represent the angles. This law is particularly useful for non-right triangles, or oblique triangles, which are any triangles that are not right triangles.
The Law of Sines states that the ratio of the side length of a triangle to the sine of the opposite angle is the same for all three sides. In other words, if we divide side 'a' by the sine of angle 'A', it is equal to dividing side 'b' by the sine of angle 'B', which is also equal to dividing side 'c' by the sine of angle 'C'.
This rule can be used to solve for unknown sides or angles in a triangle when certain combinations of measurements are given. For example, if we know the value of one side and the values of two angles, we can use the Sine Rule to find the length of the unknown side.
The Sine Rule is derived from the right triangle trigonometric relationships, where sine is defined as the ratio of the side opposite an angle to the hypotenuse. However, the rule is applicable to all types of triangles, not just right triangles.
In summary, the Sine Rule formula, a/Sin A = b/Sin B = c/Sin C, is a powerful tool for solving oblique triangles by relating the sides and angles of a triangle.
Exploring the Application of Mail Laws to Emails
You may want to see also
Frequently asked questions
Yes, the law of sines can be used for right triangles. It is also known as the "Sine Rule" and it defines the ratio of sides of a triangle and their respective sine angles.
The law of sines is one of the most useful triangle equations. It allows us to make calculations based on the angles of triangles rather than their sides. It is particularly helpful when we want to find unknown sides or angles of a triangle.
The formula for the law of sines is:
(Sin A/a) = (Sin B/b) = (Sin C/c)
To solve a triangle using the law of sines, you need to know either two angles and one side, or two sides and a non-included angle. You can then set up a proportion to solve for the unknown side or angle.







