Ohm's Law And Ac: What's The Relationship?

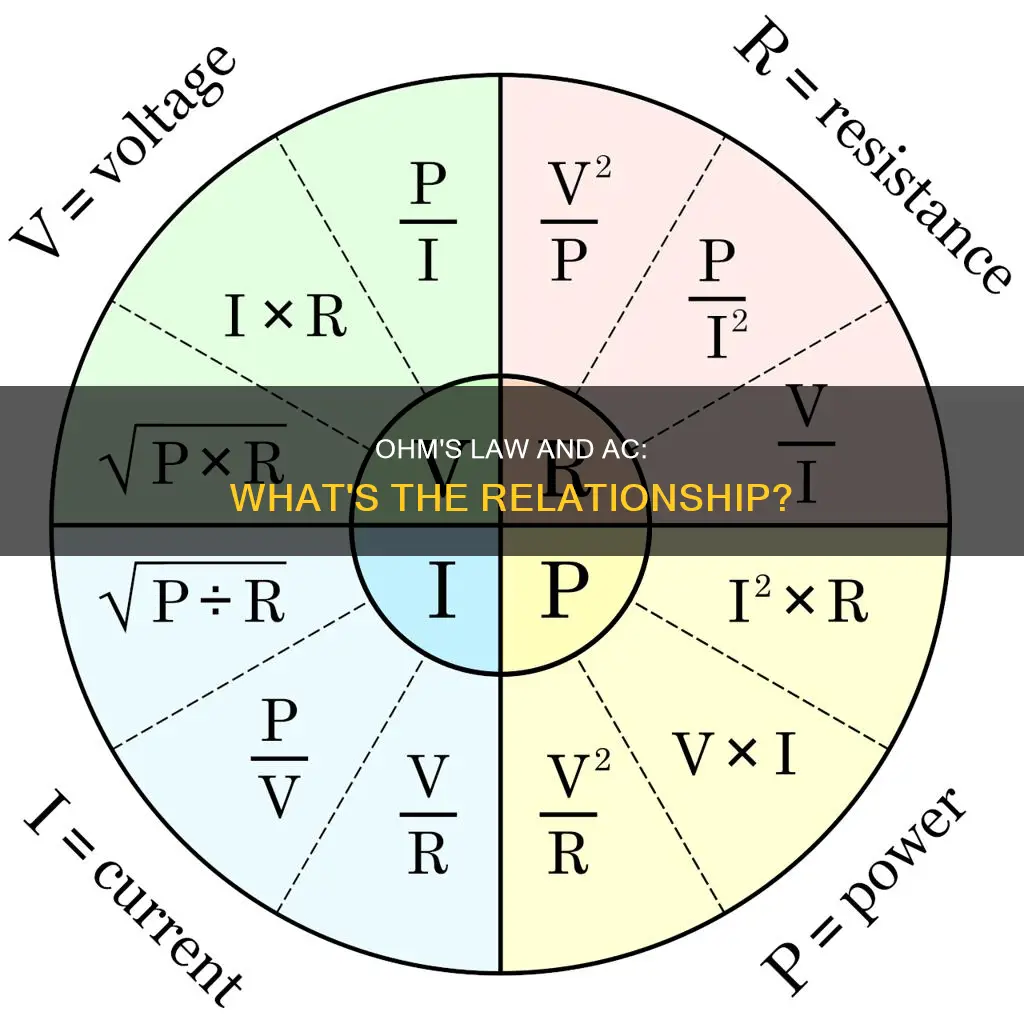
Ohm's law applies to both direct current (DC) and alternating current (AC) circuits. However, the formula for calculating power differs between the two: for DC, the formula is P = VI = V^2/R = I^2*R, while for AC, it is P = VIcos. In AC circuits, the law is expressed as V = IZ, where Z is the impedance, and V and I are the RMS or effective values of voltage and current. Impedance is the ratio of the voltage and current peaks, but the peaks do not occur simultaneously, so a phase angle is necessary to characterise the circuit.

Ohm's Law applies to AC circuits, but the formula is different

Ohm's Law applies to both AC and DC circuits. However, the formula for AC circuits is different.

Ohm's Law states that the current flowing through a circuit is proportional to the voltage applied across the circuit. In other words, the ratio of voltage to current is always constant. This law holds true for both AC and DC circuits, but the formula used to calculate it differs.

For DC circuits, the formula is:

> R = Resistance of the circuit

> V = IR

Where I is the current and R is the resistance.

However, for AC circuits, the formula becomes:

> Z = Net impedance of the circuit (including the effect of mutual inductance)

> V = IZ

Where Z is the net impedance of the circuit, which includes resistance, inductive reactance, and capacitive reactance. Inductive reactance and capacitive reactance are forms of electrical opposition that are different from normal resistance and change with the AC frequency.

The AC formula also involves complex sources and impedances, which vary with time or frequency. This means that V, I, and R are not always real numbers but can be complex expressions.

Additionally, the AC formula requires taking into account the phase angle, which is necessary to characterize the circuit and calculate the average power used. This phase angle indicates that even though Z is the ratio of the voltage and current peaks, these peaks do not occur simultaneously.

Therefore, while Ohm's Law applies to both types of circuits, the formula for AC circuits involves additional considerations and calculations to account for the unique characteristics of alternating current.

AC circuits have complex sources and impedances which vary with time or frequency

AC circuits have complex sources and impedances that vary with time or frequency. Impedance is the term used to describe the opposition to the flow of alternating electrical current in an AC circuit. It is measured in ohms and is influenced by resistance, inductance, and capacitance.

In a DC circuit, resistance is the term used to describe the opposition to current flow. However, in an AC circuit, the presence of reactive components such as inductors and capacitors results in a more complex relationship between voltage and current. This is where the concept of impedance comes into play.

The impedance of a circuit is determined by the combined effects of resistance (R) and reactance (X). While resistance remains constant, reactance can change with frequency. Inductive reactance increases with frequency, while capacitive reactance decreases. This variation in reactance means that the overall impedance of an AC circuit is not simply the sum of resistance and reactance; instead, they are combined using vector addition, resulting in a phase difference between the two.

The impedance of a circuit can be calculated using complex numbers, with the formula Z = R + jX, where Z is the impedance, R is the resistance, j is the imaginary unit, and X is the reactance. This complex representation allows for a more comprehensive analysis of AC circuits, taking into account both the magnitude and phase of the impedance.

Ohm's Law, which states that the current flowing through a circuit is proportional to the voltage applied across it, can be applied to both DC and AC circuits. In an AC circuit, the expression becomes more complex, taking into account the net impedance of the circuit, which includes the effect of mutual inductance.

In summary, while AC circuits introduce additional complexity with their varying impedances, Ohm's Law still holds true. The key difference lies in the expressions used to calculate resistance and impedance, with R being used for DC circuits and Z (which includes the effects of reactance) being used for AC circuits.

AC circuits involve time-varying voltages and currents

AC circuits, unlike their DC counterparts, involve time-varying voltages and currents. This means that the voltage and current in an AC circuit change over time, resulting in a more complex behaviour compared to DC circuits.

In an AC circuit, the relationship between voltage and current is described by Ohm's Law, which states that the current flowing through a circuit is proportional to the voltage applied across it. However, in an AC circuit, this relationship becomes more intricate due to the presence of complex sources and impedances. Impedance, denoted as Z, is a measure of the opposition to the flow of alternating current and includes both resistance and reactance. Reactance, on the other hand, is the opposition to the flow of current due to inductors and capacitors, which can cause a phase shift between the voltage and current.

Ohm's Law for AC circuits takes the form of V = IZ, where V is the voltage, I is the current, and Z is the impedance. This equation considers the time-varying nature of AC voltages and currents and accounts for the effects of inductors and capacitors. By using complex numbers and phasors, we can describe the magnitude and phase of the voltage and current in an AC circuit.

It is important to note that the impedance of an AC circuit may vary with time or frequency, resulting in complex expressions for V, I, and Z. Nevertheless, the fundamental relationships established in Ohm's Law for DC circuits remain applicable in AC circuits.

Additionally, when dealing with AC circuits, it is crucial to consider the frequency of the AC signal. At high frequencies, such as radio frequencies, the current density in wires can no longer be assumed to be constant across the cross-section of a wire. This phenomenon, known as the "skin effect", occurs due to significant magnetic effects and must be taken into account when designing high-frequency circuits.

In AC circuits, Ohm's Law is V = IZ, where Z is impedance

Ohm's Law applies to both DC and AC circuits. However, in AC circuits, the law is expressed as V = IZ, where Z is the impedance of the circuit. Impedance is a measure of the opposition to the flow of AC current and includes resistance, inductive reactance, and capacitive reactance.

In AC circuits, the voltage and current are time-varying and can be out of phase, which means they do not rise and fall in sync. This is why the formula for Ohm's Law in AC circuits includes impedance, which takes into account the effects of inductors and capacitors, in addition to resistance.

The formula for impedance, Z, is given as Z = R + jX, where R is resistance, j is the imaginary number, and X is the reactance, which includes both inductive and capacitive reactance.

Ohm's Law in AC circuits is valid for typical wires and elements used in household electricity, which is at 60Hz frequency. At this frequency, the current density in wires can be assumed to be constant across the cross-section of a wire. However, at high frequencies, such as radio frequencies, the magnetic effects become significant, and the current is predominantly in the outer parts of the conductors, an effect known as the "skin effect". Therefore, for high-frequency circuits, this effect must be considered in the design.

Impedance includes resistance, inductive reactance and capacitive reactance

Impedance is a measure of how much a circuit resists or impedes the flow of charge. It is denoted by the symbol Z and measured in ohms (Ω). Impedance includes resistance, inductive reactance, and capacitive reactance.

Resistance is the opposition to the flow of current in a circuit and is denoted by R. It is always positive and remains constant regardless of frequency. Resistance is the real part of impedance.

Reactance, on the other hand, is the opposition to the flow of current due to inductance and capacitance in a circuit. It is denoted by X and can be either positive or negative. Reactance is the imaginary part of impedance.

Inductive reactance is caused by inductors, which store electrical energy in the form of a magnetic field. Inductors cause the current to lag behind the voltage by 90 degrees. The reactance of an ideal inductor is positive for all frequencies and its impedance increases with frequency.

Capacitive reactance is caused by capacitors, which store electrical energy in the form of an electric field. Capacitors cause the voltage to lag behind the current by 90 degrees. The reactance of an ideal capacitor is negative for all frequencies and its impedance decreases with frequency.

Ohm's Law, which states that the current flowing through a circuit is proportional to the voltage applied across it, applies to both DC and AC circuits. However, in AC circuits, the concept of impedance, which includes resistance and reactance, is used to account for the effects of inductance and capacitance. The formula for impedance is Z = R + jX, where R is resistance, j is the imaginary unit, and X is reactance.

Frequently asked questions