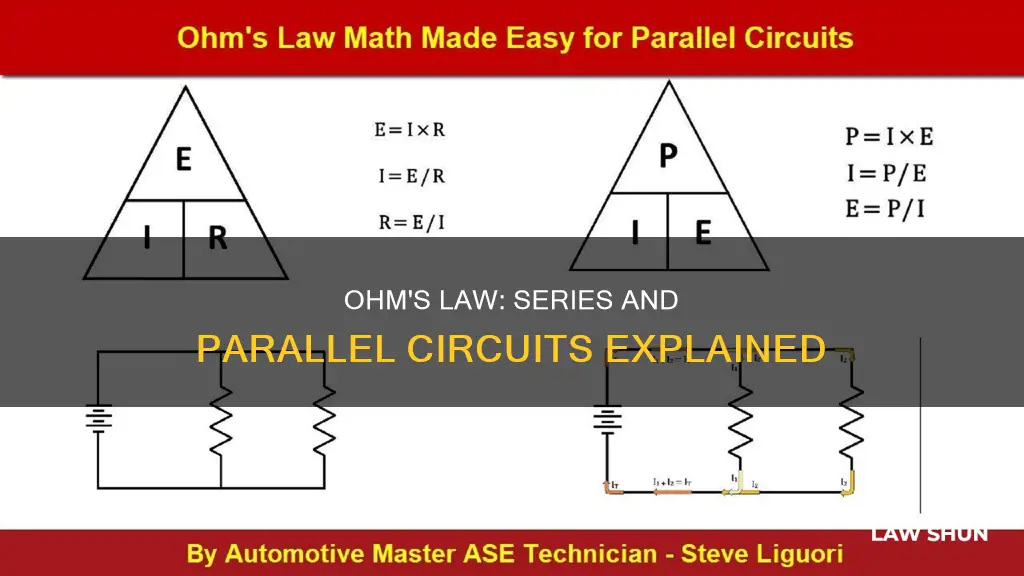
Ohm's Law, named after Georg Ohm, is a formula used to determine the relationship between voltage, current, and resistance in an electrical circuit. Ohm's Law is particularly helpful when resistance needs to be calculated as it cannot be measured in an active circuit. When applying Ohm's Law to series and parallel circuits, it is important to remember that the variables used in the equations must be common to the same two points in the circuit under consideration. In a series circuit, the current is the same through each component, and the total resistance is equal to the sum of the individual resistances. On the other hand, in a parallel circuit, the voltage is the same across all components, and the total current is the sum of all the individual branch currents.
| Characteristics | Values |
|---|---|
| Series Circuit | All components are connected end-to-end to form a single path for current flow |
| Series Circuit | The total resistance is equal to the sum of the individual resistors |
| Series Circuit | The total voltage drop is equal to the sum of the individual voltage drops |
| Series Circuit | The current is the same through each component |
| Parallel Circuit | All components share the same electrical nodes |
| Parallel Circuit | The voltage is the same across all components |
| Parallel Circuit | The total circuit current is the sum of the individual branch currents |
| Parallel Circuit | The total resistance is less than any of the individual branch resistances |
What You'll Learn

Ohm's Law and Kirchhoff's Voltage Law
Kirchhoff's Voltage Law states that the sum of the voltage drops in a closed circuit is equal to the voltage supplied by the source. In other words, in a series of connected components, the total voltage supplied is equal to the sum of the voltage drops across each component. This is represented as: Voltage Supplied (Vs) = Voltage Drop 1 (VD1) + Voltage Drop 2 (VD2) +...
When applying Ohm's Law to series and parallel circuits, it is important to remember that the variables used in the equations must be common to the same two points in the circuit under consideration. In a series circuit, the total resistance is calculated by adding up the individual resistances, resulting in a total resistance greater than any single resistor in the circuit. The total current in a series circuit remains the same throughout, and the voltage supplied is equal to the sum of the individual voltage drops.
On the other hand, in a parallel circuit, all components share the same electrical nodes, resulting in the same voltage across all components. The total current in a parallel circuit is the sum of the individual branch currents, and the total resistance is calculated differently, resulting in a value less than any single resistor in the circuit.
By applying Ohm's Law and Kirchhoff's Voltage Law, engineers can determine the voltage, current, resistance, and power in complex series and parallel circuits, aiding in the design and analysis of electrical systems.
Understanding Age Discrimination Laws: Employee Rights and Protections
You may want to see also

Calculating total resistance in a series circuit
Ohm's Law states that the voltage across a component is found by multiplying the current and resistance in a circuit or component. In other words, V=IxR, R=V/I, and I=V/R, where V = voltage, I = current, and R = resistance.
When applying Ohm's Law to a series circuit, it is important to remember that the total resistance of a series circuit is equal to the sum of the individual resistances. This means that the current flowing in each circuit element is the same across the circuit.
For example, let's say we have a series circuit with three resistors, R1, R2, and R3, with values of 4 Ω, 3 Ω, and 6 Ω, respectively. To calculate the total resistance, we simply add up the individual resistances:
> R_total = R1 + R2 + R3 = 4 Ω + 3 Ω + 6 Ω = 13 Ω
So, the total resistance of this series circuit is 13 Ω.
It is worth noting that the equivalent resistance of a series circuit is always higher than any of its individual components. This is in contrast to a parallel circuit, where the total resistance is less than any of the individual resistances.
Additionally, when working with complex series and parallel circuits, it is important to remember that the variables used in Ohm's law equations must be common to the same two points in the circuit under consideration. This means that when calculating the resistance of a single component, you should ensure that the voltage, current, and resistance are specific to that component alone.
By following these guidelines and applying Ohm's Law, you can accurately calculate the total resistance in a series circuit.
Sonography's Legal and Ethical Challenges: A Guide
You may want to see also

Calculating total resistance in a parallel circuit
Ohm's Law states that the voltage across a component is equal to the product of the current flowing through it and its resistance, i.e., V = IR. This law can be applied to both series and parallel circuits.
In a parallel circuit, the voltage is the same across all components, and the total current is the sum of all the individual branch currents. The total resistance of a parallel circuit is less than any of the individual branch resistances.
The formula for calculating the total resistance of a parallel circuit is:
$$R_{total} = \frac{1}{\frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}}$$
Where:
R1, R2, and R3 are the resistances of the individual branches.
To calculate the total resistance of a parallel circuit, follow these steps:
- Take the reciprocal of each branch resistance value.
- Add these reciprocal values together.
- Take the reciprocal of the sum to find the total resistance.
For example, let's consider a parallel circuit with three branches having resistances of 10 Ω, 2 Ω, and 1 Ω, respectively.
Using the formula:
$$\frac{1}{R_{total}} = \frac{1}{10} + \frac{1}{2} + \frac{1}{1}$$
First, convert the fractions to a common denominator:
$$\frac{1}{R_{total}} = \frac{1}{10} + \frac{5}{10} + \frac{10}{10} = \frac{16}{10} = 1.6$$
Now, multiply both sides by Rtotal:
$$1 = 1.6 \times R_{total}$$
$$R_{total} = \frac{1}{1.6} = 0.625 \, \Omega$$
So, the total resistance of the parallel circuit is 0.625 Ω.
It's important to note that the total resistance of a parallel circuit is always less than the resistance of any individual branch. This is because each parallel resistor added to the circuit provides an additional path for the current to flow, reducing the overall resistance.
Security Deposit Laws: Sublease Rights and Responsibilities
You may want to see also

Calculating total current in a series circuit
Ohm's Law states that the voltage between two points is equal to the product of the current and resistance between those points. In other words, V = IR, where V is the voltage, I is the current, and R is the resistance.
When calculating the total current in a series circuit, it's important to remember that the total resistance is the sum of the individual resistances. So, if you have three resistors in series, R1, R2, and R3, the total resistance (R-total) is equal to R1 + R2 + R3.
The total voltage in a series circuit is also the sum of the individual voltages. So, if you have voltages V1, V2, and V3, the total voltage (V-total) is equal to V1 + V2 + V3.
Once you have the total resistance and voltage, you can use Ohm's Law to calculate the total current (I-total). The formula for this is:
I-total = V-total / R-total
For example, let's say you have a series circuit with three resistors: R1 = 10Ω, R2 = 2Ω, and R3 = 9Ω. If the total voltage applied to the circuit is 2.5V, you can calculate the total current as follows:
First, find the total resistance:
R-total = 10Ω + 2Ω + 9Ω = 21Ω
Now, use Ohm's Law to find the total current:
I-total = V-total / R-total = 2.5V / 21Ω = 0.119A or 119mA
So, the total current in the circuit is 0.119 Amperes or 119 milliAmperes.
It's important to note that in a series circuit, the current is the same through all the components. This is because there is only one path for the current to flow.
Understanding Series Circuits with Ohm's Law
You may want to see also

Calculating total current in a parallel circuit
In a parallel circuit, the total current is the sum of all the individual branch currents. This is because the total current exiting the positive battery terminal splits into multiple branches, and the combined flow rates of all branches must equal the flow rate of the whole river.
To calculate the total current, you can use the following formula:
IT = I1 + I2 + I3 + ...
Where:
- IT is the total current
- I1, I2, I3, etc. are the currents in each branch
For example, let's say we have a parallel circuit with three resistors, R1, R2, and R3, with the following currents:
- IR1 = 0.9 mA
- IR2 = 4.5 mA
- IR3 = 9.0 mA
To find the total current, we would add up these individual branch currents:
IT = IR1 + IR2 + IR3
IT = 0.9 mA + 4.5 mA + 9.0 mA
IT = 14.4 mA
So, the total current in this parallel circuit is 14.4 mA.
It's important to note that in a series circuit, the total current is the same through all the components, whereas in a parallel circuit, the total current is the sum of the individual branch currents.
Men's Legal Responsibilities: Unique Laws for Men?
You may want to see also
Frequently asked questions
Ohm's law relates the resistance of a component to its voltage and current. It allows us to formulate rules to determine total resistance.
In a series circuit, all components are connected to form a single path for current flow. The total resistance in a series circuit is the sum of the individual resistances, and the total voltage drop is equal to the sum of the individual voltage drops across those resistors.
In a parallel circuit, all components share the same electrical nodes, so the voltage is the same across all components. The total current is the sum of all the individual branch currents, and the total resistance is less than any of the individual branch resistances.
In a series circuit, there is only one path for the current to flow, whereas a parallel circuit has multiple paths.
The total resistance of a series circuit is equal to the sum of the individual resistances.