The law of sines, also known as the sine rule, sine formula, or sine law, is a trigonometric equation that relates the lengths of the sides of a triangle to the sines of its angles. The law of sines applies to all triangles, including right triangles, and can be used to find the unknown angle or side of a triangle.
| Characteristics | Values |
|---|---|
| Definition | The law of sines defines the ratio of sides of a triangle and their respective sine angles are equivalent to each other. |
| Other names | Sine law, sine rule, sine formula |
| Purpose | Used to find the unknown angle or the side of an oblique triangle (non-right triangle) |
| Formula | a/sin A = b/sin B = c/sin C |
| General formula | a sin A = b sin B = c sin C |
| Application | Used in engineering, astronomy and navigation |
What You'll Learn

The law of sines can be used to find unknown sides or angles
The law of sines, also known as the sine rule, sine formula, or sine law, is a trigonometric equation that relates the lengths of a triangle's sides to the sines of its angles. The law of sines can be used to find unknown sides or angles of a triangle when certain combinations of measurements are given.
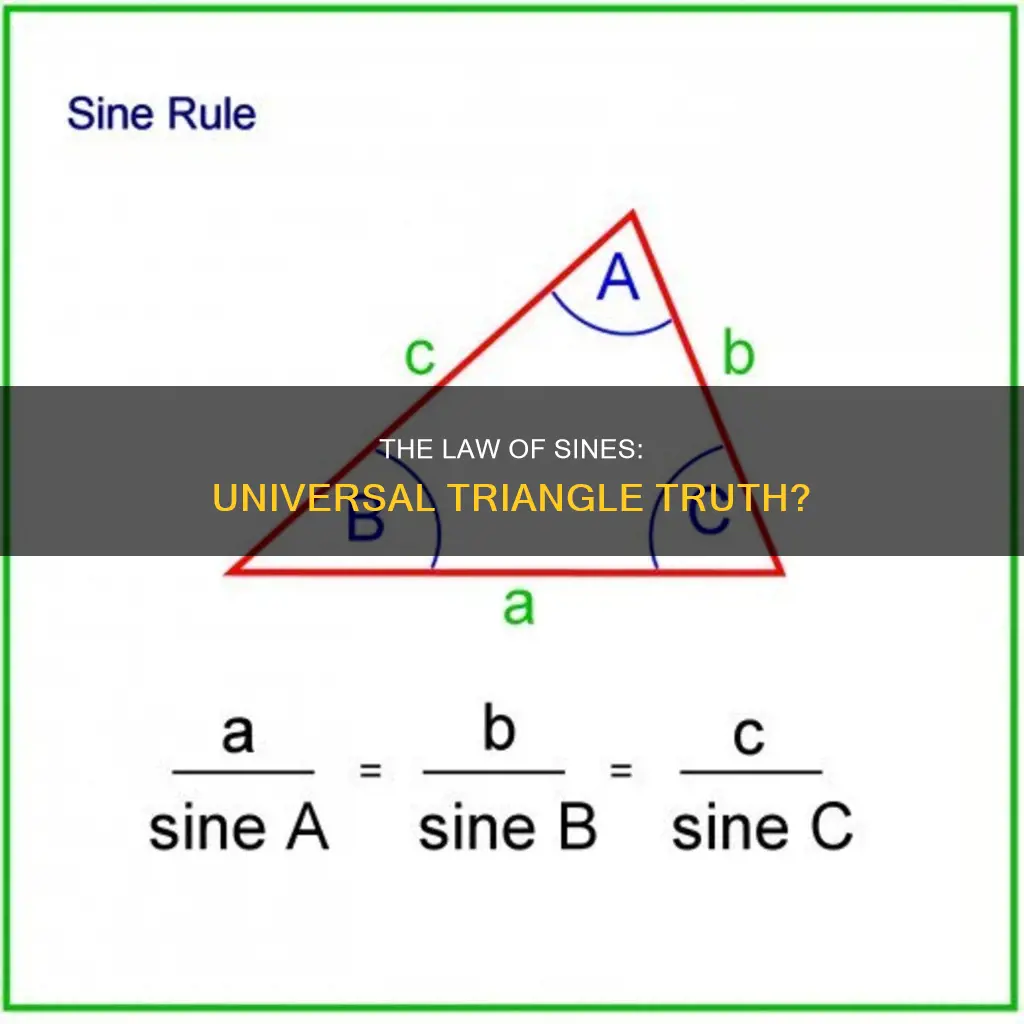
The law of sines is defined as the ratio of side length to the sine of the opposite angle, and it holds for all three sides of a triangle regardless of their sides and angles. The formula for the law of sines is:
A/sin A = b/sin B = c/sin C
Here, a, b, and c represent the lengths of the sides of the triangle, and A, B, and C are the angles opposite those sides. This formula can be rearranged in three different ways:
A/sinA = b/sinB = c/sinC
SinA/a = sinB/b = sinC/c
A/b = sinA/sinB; a/c = sinA/sinC; b/c = sinB/sinC
For example, let's say we have a triangle with side a = 7 cm, angle A = 60 degrees, and angle B = 45 degrees. Using the law of sines formula, we can find the length of side b:
7/sin 60° = b/sin 45°
7/(√3/2) = b/(1/√2)
B = 14/(√3√2) = 14/√6
So, the length of side b is approximately 14/√6.
The law of sines is a valuable tool for solving triangles and can be applied in various fields, including engineering, astronomy, and navigation.
Lemon Laws and Vans: What's the Verdict?
You may want to see also

The law of sines is also known as the sine rule
The law of sines, also known as the sine rule, is an equation relating the lengths of the sides of any triangle to the sines of its angles. The Persian mathematician Nasir al-Din al-Tusi was the first to state and prove the law of sines, which applies to all plane triangles.
The law of sines can be used to compute the remaining sides of a triangle when two angles and a side are known, or when two sides and one non-enclosed angle are known. In some cases, the triangle is not uniquely determined by this data (the ambiguous case) and the technique gives two possible values for the enclosed angle.
The law of sines can be used to find the unknown angle or unknown side of a triangle. This law can be used if certain combinations of measurements of a triangle are given. The sine rule formula gives the ratio of the sides and angles of a triangle. The sine rule can be explained using the expression:
A/sinA = b/sinB = c/sinC
Here, a, b, c are the length of the sides of the triangle, and A, B, C are the angles of the triangle.
The sine rule can be represented in three different forms:
- A/sinA = b/sinB = c/sinC
- SinA/a = sinB/b = sinC/c
- A/b = sinA/sinB; a/c = sinA/sinC; b/c = sinB/sinC
The sine rule is helpful in finding the sides of a triangle when two angles and one side of a triangle are known. This technique is known as triangulation. The sine law in trigonometry should not be confused with the sine law in physics.
The law of sines can also be used to find the area of an oblique triangle. The area of a triangle = (1/2)ab sinC = (1/2)bc sinA = (1/2)ca sinB.
Implied Consent Law: Who Does It Affect?
You may want to see also

The formula for the law of sines
The law of sines, also known as the sine rule, sine formula, or sine law, is an equation that relates the lengths of the sides of a triangle to the sines of its angles.
$$\frac{a}{\sin \alpha} = \frac{b}{\sin \beta} = \frac{c}{\sin \gamma} = 2R$$
Where:
- A, b, and c are the lengths of the sides of a triangle
- Α, β, and γ are the angles opposite their respective sides
- R is the radius of the triangle's circumcircle
The formula can also be written in its reciprocal form:
$$\frac{\sin \alpha}{a} = \frac{\sin \beta}{b} = \frac{\sin \gamma}{c}$$
The law of sines can be used to find the unknown sides or angles of a triangle when two angles and one side are known, or when two sides and one non-enclosed angle are known.
The formula can be applied to all types of triangles, including right triangles and oblique triangles.
Zoning Laws: Do They Affect Your Web Store?
You may want to see also

The law of sines can be used on right triangles
The law of sines, also known as the sine rule, sine law, or sine formula, is defined as the ratio of side length to the sine of the opposite angle. It holds for all three sides of a triangle, regardless of their sides and angles.
The law of sines can be used to find the unknown angle or side of an oblique triangle, which is any triangle that is not a right triangle. It should be noted that the trigonometric functions are typically defined in terms of right triangles only.
The law of sines formula can be written as:
- A/Sin A = b/Sin B = c/Sin C
- Sin A/a = Sin B/b = Sin C/c
The law of sines can be used to solve oblique triangles, which are non-right triangles, and is particularly useful when we know two angles and one side or two angles and one included side. This is known as the ASA (Angle-Side-Angle) or AAS (Angle-Angle-Side) criteria, respectively.
In the case of a right triangle, the law of sines still applies and is valid. However, it may not be the most interesting or efficient approach as it becomes largely redundant due to the definitions of sine and cosine in terms of right triangles.
For example, let's consider a right triangle with a right angle at angle C and side AB = c, BC = a, and AC = b. To prove the law of sines, we can draw a perpendicular CD ⊥ AB, where CD = h is the height of the triangle. This separates the triangle ABC into two right-angled triangles, CDA and CDB.
Now, let's calculate Sin A/Sin B:
Sin A/Sin B = (h/b)/(h/a) = a/b
Similarly, we can prove that Sin B/Sin C = b/c and so on for any pair of angles and their opposite sides.
Therefore, the law of sines can be used on right triangles, but it is more commonly applied to oblique triangles where it provides a useful method for solving triangles when other approaches may be more complex.
Labor Laws: Contractors and the Fine Print
You may want to see also

The law of sines can be used to find the area of a triangle
> "T = (1/2) ab sin θ, where θ is the angle enclosed by the sides of lengths a and b."
Substituting the sine law into this formula gives:
> "T = (1/2) ab x (c/2R) = abc/4R."
Here, R is the radius of the circumcircle.
The law of sines can also be used to find the area of an oblique triangle. The formula for this is:
> "Area of triangle = (1/2) ab sin C = (1/2) bc sin A = (1/2) ca sin B."
The sine law can be applied to any triangle, including right triangles, to establish a relationship between the ratios of sides and their respective opposite angles.
Fair Housing Law: Does It Apply to Your Home?
You may want to see also