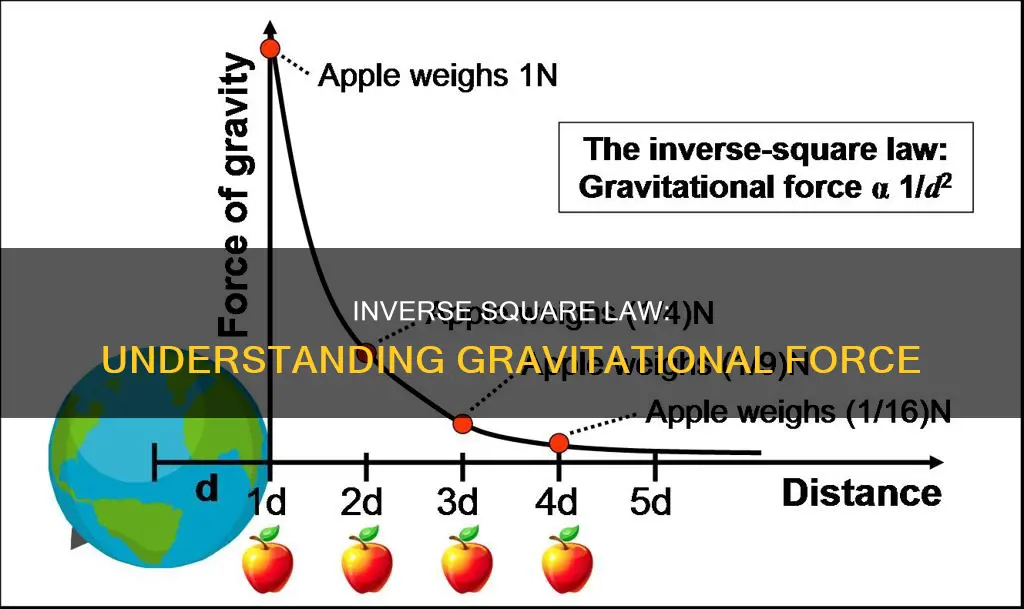
The inverse square law is a scientific law that states that the intensity of a physical quantity is inversely proportional to the square of the distance from its source. In other words, as the distance from the source of a physical quantity, such as energy or force, doubles, its intensity is divided by four. This law applies to diverse phenomena, including gravitational force, electric fields, light, sound, and radiation. Newton's law of universal gravitation, which states that the gravitational force between two bodies is directly proportional to the product of their masses and inversely proportional to the square of their separation, follows the inverse square law. The law can be expressed mathematically as F = GMm/r^2, where F is the force, G is Newton's gravitational constant, M and m are the masses of the objects, and r is the distance between them.
| Characteristics | Values |
|---|---|
| The inverse square law applies to | Point sources of gravitational force, electric field, light, sound or radiation |
| The intensity of the influence at any given radius r | The source strength divided by the area of the sphere |
| The effect of gravity | Inversely proportional to the square of their separation distance |
| The two things that control gravity | Mass and distance |
What You'll Learn
- The inverse square law applies to gravitational force because it is a point source
- The intensity of the influence at any radius is the source strength divided by the area of the sphere
- The inverse square law can be used to calculate the gravitational force between two bodies
- The inverse square law is used to understand the role of gravity in creating stable elliptical orbits
- The inverse square law can be applied to other forces, such as sunlight

The inverse square law applies to gravitational force because it is a point source
The inverse square law states that the intensity of a physical quantity is inversely proportional to the square of the distance from the source of that physical quantity. In the case of gravitational force, the source is a point mass. The law can be expressed mathematically as:
> {\displaystyle {\text{intensity}}\ \propto \ {\frac {1}{{\text{distance}}^{2}}}\,}
Or:
> {\displaystyle {\frac {{\text{intensity}}_{1}}{{\text{intensity}}_{2}}}={\frac {{\text{distance}}_{2}^{2}}{{\text{distance}}_{1}^{2}}}}
The law essentially describes the geometric dilution of a point source's radiation into three-dimensional space. As the emitted radiation moves farther from the source, it spreads out over an increasingly large area. Therefore, the intensity of radiation passing through any unit area is inversely proportional to the square of the distance from the point source.
The inverse square law can be applied to gravitational force by considering the force to be the intensity of the influence at any given radius. This influence is the source strength (mass) divided by the area of the sphere. As the distance from the point mass increases, the area of the sphere increases as the square of the radius, and so the intensity of the gravitational force decreases proportionally.
This is why the gravitational force between two bodies is inversely proportional to the square of their separation distance.
Laws and Their Application: Understanding the Basics
You may want to see also

The intensity of the influence at any radius is the source strength divided by the area of the sphere
The inverse square law is a scientific principle that explains the relationship between the intensity of a physical quantity and its distance from the source. According to this law, the intensity of a physical quantity or influence is inversely proportional to the square of the distance from its source. In other words, as the distance from the source increases, the intensity decreases. This law is based on the geometric dilution of point-source radiation into three-dimensional space.
The law can be expressed mathematically as:
> {\displaystyle {\text{intensity}}\ \propto \ {\frac {1}{{\text{distance}}^{2}}}\,}
Now, let's focus on the statement: "The intensity of the influence at any radius is the source strength divided by the area of the sphere."
This statement describes a key aspect of the inverse square law. The "intensity of influence" refers to the strength or power of a particular phenomenon, such as gravitational force, electric field, light, sound, or radiation, at a certain distance from its source. The "source strength" represents the potency or magnitude of the source that generates this influence. Meanwhile, the "area of the sphere" pertains to the spatial extent of the influence as it spreads out from the source.
At any given radius (distance) from the source, the intensity of the influence is determined by dividing the source strength by the area of the sphere at that radius. This calculation takes into account the dilution or dispersion of the influence as it expands into three-dimensional space. By considering the area of the sphere, we account for the spreading out of the influence over a larger and larger area as the distance from the source increases.
For example, let's consider a point source of light. As the light radiates outward in all directions, it spreads over an increasingly larger spherical area. Consequently, the intensity of illumination decreases as you move away from the source. This decrease in intensity follows the inverse square law, where the intensity is inversely proportional to the square of the distance from the light source.
The same principle applies to gravitational force. According to Newton's law of universal gravitation, the gravitational attraction force between two masses is directly proportional to the product of their masses and inversely proportional to the square of the distance between them. Therefore, as objects with mass get farther apart, the gravitational force between them weakens, following the inverse square law.
The inverse square law has broad applications and is essential for understanding various natural phenomena. It helps explain how different types of waves, such as light and sound, propagate and how their intensity diminishes with distance. Additionally, it plays a crucial role in fields like telecommunications, medical imaging, and astrophysics, where understanding the behaviour of gravitational forces is vital.
The Law of Moses: Still Relevant Today?
You may want to see also

The inverse square law can be used to calculate the gravitational force between two bodies
Mathematically, this can be expressed as:
> {\displaystyle {\text{intensity}}\ \propto \ {\frac {1}{{\text{distance}}^{2}}}\,}
Or, in terms of specific intensities and distances:
> {\displaystyle {\frac {{\text{intensity}}_{1}}{{\text{intensity}}_{2}}}={\frac {{\text{distance}}_{2}^{2}}{{\text{distance}}_{1}^{2}}}}
This can also be written as:
> {\displaystyle {\text{intensity}}_{1}\times {\text{distance}}_{1}^{2}={\text{intensity}}_{2}\times {\text{distance}}_{2}^{2}}
In the context of gravitational force, the physical quantity of interest is the force of gravity, and the source of this quantity is the object exerting the gravitational force. Therefore, the inverse square law can be applied to calculate the gravitational force between two objects by considering the distance between them.
The formula for gravitational force between two objects, as described by Newton's law of universal gravitation, is:
> F = GMm/r^2
Where F is the force, G is Newton's gravitational constant, M and m are the masses of the objects, and r is the distance between them.
This formula illustrates that the gravitational force between two objects is directly proportional to the product of their masses and inversely proportional to the square of the distance between them. This inverse proportionality with the square of the distance aligns with the inverse square law.
By applying this formula and considering the masses and distance between two bodies, the gravitational force between them can be calculated.
Kepler's Second Law: Universal or Unique?
You may want to see also

The inverse square law is used to understand the role of gravity in creating stable elliptical orbits
The inverse square law is a scientific law that states that the "intensity" of a physical quantity is inversely proportional to the square of the distance from the source of that physical quantity. In other words, as the distance from the source of a physical quantity, such as gravitational force, increases, the intensity of that force decreases. This law is based on geometric dilution, which corresponds to point-source radiation into three-dimensional space.
The inverse square law can be applied to understand the role of gravity in creating stable elliptical orbits. Gravity is the force that keeps objects in orbit around a larger body, such as a planet orbiting the Sun. The inverse square law explains that the force of gravity between two bodies is directly proportional to the product of their masses and inversely proportional to the square of their separation distance. This means that as the distance between two objects increases, the gravitational force between them decreases.
For example, let's consider a planet orbiting the Sun. As the planet moves further away from the Sun, the gravitational force between them weakens according to the inverse square law. However, the planet also needs to be moving at a velocity greater than the pull of the Sun to maintain its orbit. If the planet were to move closer to the Sun, the gravitational force would increase, and the planet would need to increase its velocity to maintain a stable orbit.
The inverse square law also applies to other forces, such as sunlight. Using the previous example, if the planet were to move three times closer to the Sun, it would receive nine times the amount of sunlight (the square of 3 is 9). This is because the intensity of sunlight is inversely proportional to the square of the distance from the source, in this case, the Sun.
By understanding the inverse square law and its application to gravitational force, scientists can predict and explain the stable elliptical orbits of objects in space. This law helps explain how planets maintain their orbits around stars, how moons orbit planets, and how artificial satellites can remain in stable orbits around Earth or other celestial bodies.
Competition Law: EU's Influence on the UK
You may want to see also

The inverse square law can be applied to other forces, such as sunlight
The inverse square law is a scientific law that states that the "intensity" of a physical quantity is inversely proportional to the square of the distance from the source of that physical quantity. In other words, the intensity of the influence at any given radius is the source strength divided by the area of the sphere.
The law generally applies when a force, energy, or other conserved quantity is evenly radiated outward from a point source in three-dimensional space. As the emitted radiation moves away from the source, it is spread out over an area that is proportional to the square of the distance from the source. This means that the intensity of radiation passing through any unit area is inversely proportional to the square of the distance from the point source.
The inverse square law can also be applied to other phenomena, such as electric fields, sound, and radiation. In the case of electric fields, the electric force follows the inverse square law, where the force between two electrically charged particles is inversely proportional to the square of the distance between them. For sound, the inverse square law applies to the intensity of sound waves radiating from a point source. The law also applies to radiation exposure from a point source, where the exposure decreases as the distance from the source increases.
Unclaimed Property Laws: Do Massachusetts Non-Profits Comply?
You may want to see also
Frequently asked questions
The inverse square law is a scientific law that states that the "intensity" of a physical quantity is inversely proportional to the square of the distance from the source of that physical quantity.
The inverse square law applies to gravitational force because the force of gravitation between two bodies is proportional to the product of their masses and inversely proportional to the square of their separation.
The formula for the inverse square law is: F = GMm/r^2, where F is the force, G is Newton's gravitational constant, M and m are the masses of the objects, and r is the distance between them.