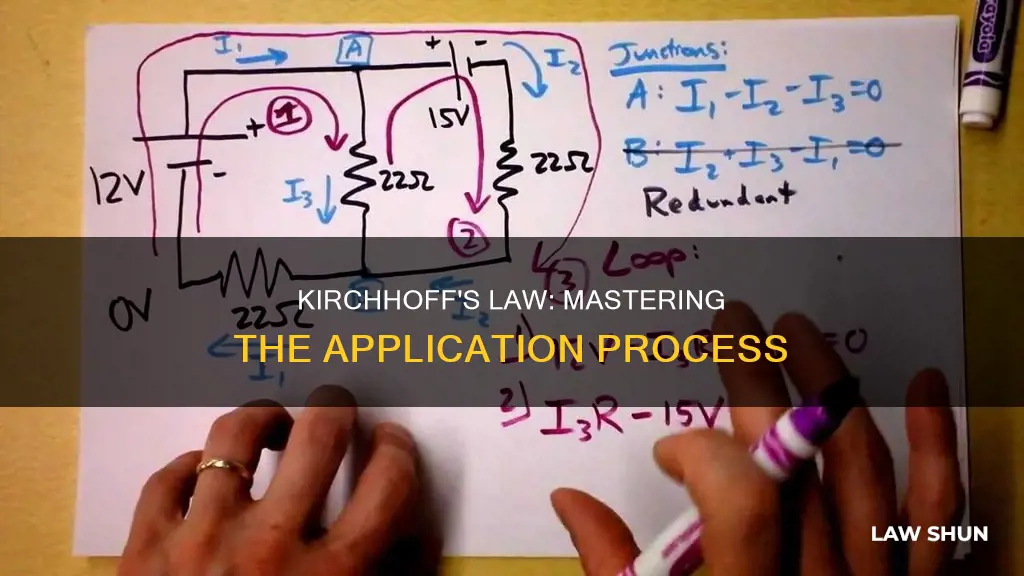
Kirchhoff's Circuit Laws are a set of rules that allow us to solve complex circuit problems by defining a set of basic network laws and theorems for the voltages and currents around a circuit. These laws are especially useful when Ohm's Law falls short, such as when dealing with circuits that have both parallel and series resistance, or when there is no constant current source.
The two laws are:
- Kirchhoff's Current Law (KCL) — the total current entering a junction or node is exactly equal to the charge leaving the node.
- Kirchhoff's Voltage Law (KVL) — the total voltage around a closed loop is equal to the sum of all the voltage drops within the same loop.
| Characteristics | Values |
|---|---|
| Inventor | Gustav Kirchhoff |
| Year | 1845 |
| First Rule | Junction Rule |
| First Rule | The sum of all currents entering a junction must equal the sum of all currents leaving the junction |
| First Rule | I(exiting) + I(entering) = 0 |
| First Rule | Conservation of Charge |
| Second Rule | Loop Rule |
| Second Rule | The algebraic sum of changes in potential around any closed circuit path (loop) must be zero |
| Second Rule | The sum of the voltages around the closed loop is equal to null |
| Second Rule | The algebraic sum of all voltage sources and voltage drops within a closed loop must be equal to zero |
| Second Rule | Conservation of Energy |
What You'll Learn
- Kirchhoff's Current Law (KCL) states that the sum of currents entering a node is equal to the sum of currents leaving the node
- KCL can be applied to analyse parallel circuits
- KCL can be used to solve for unknown currents in a circuit
- KCL simplifies complex circuits and makes unknown voltage and current calculations easier
- KCL is based on the principle of conservation of charge

Kirchhoff's Current Law (KCL) states that the sum of currents entering a node is equal to the sum of currents leaving the node
Kirchhoff's Current Law (KCL) is a fundamental principle in electrical engineering that allows us to analyse complex electrical circuits. It is named after German physicist Gustav Kirchhoff, who first described the law in 1845.
Kirchhoff's Current Law states that the sum of currents entering a node is equal to the sum of currents leaving the node. This principle is based on the conservation of charge, as current entering a node must exit the node and cannot simply disappear. In other words, what goes in must come out. This law can be applied to any node in a circuit, where a node is a junction point where two or more paths are connected via a common point.
To apply Kirchhoff's Current Law, we can follow these steps:
- Calculate the total current of the circuit: Use Ohm's Law (I = V/R) to find the total current, where V is the total voltage and R is the total resistance of the circuit.
- Calculate the current flowing through each node: Again, use Ohm's Law (I = V/R) to determine the current for each node branch.
- Compare input and output currents: By comparing the input and output currents at specific nodes, we can validate Kirchhoff's Current Law.
It is important to note that Kirchhoff's Current Law is typically used in conjunction with Kirchhoff's Voltage Law (KVL) to solve complex circuits. KVL states that the directed sum of potential differences (voltages) around any closed loop in a circuit is zero. By combining these two laws, we can analyse both the current and voltage in complex electrical circuits.
Hunting Laws: Private Property Exemption or Exception?
You may want to see also

KCL can be applied to analyse parallel circuits
Kirchhoff's Current Law (KCL) is a fundamental principle in electrical engineering that allows us to analyse complex circuits with multiple branches and nodes. It is based on the principle of conservation of charge, stating that the total current entering a node equals the total current leaving it. This law is particularly useful when dealing with circuits that cannot be simplified using Ohm's Law or series-parallel techniques.
When applying KCL to analyse parallel circuits, we consider the currents at each node, which is a junction point where two or more paths are connected. In a parallel circuit, the total current is split into multiple branches, and KCL helps us understand how this current divides and merges at each node.
Let's consider a parallel circuit with a positive "rail" and a negative "rail". At each node on the positive rail, we observe the current splitting off the main flow to each successive branch. Conversely, at each node on the negative rail, these branch currents merge together to form the main flow. This behaviour can be likened to a plumbing system, where water flow splits or merges at "tee" fittings.
By applying KCL, we can determine that the current entering a node is equal in magnitude to the current exiting it. This means that for any node, the algebraic sum of all entering and exiting currents must be zero. This principle holds true regardless of the number of currents entering or exiting the node.
To illustrate this concept, let's examine a specific node in our parallel circuit, such as node 6. At this node, we have two currents entering from the top and right, and a single current exiting to the left. Using KCL, we can set up an equation to determine the magnitude of the exiting current:
I_exit = I_enter1 + I_enter2
In this equation, I_exit represents the unknown current exiting the node, while I_enter1 and I_enter2 are the currents entering the node. By assigning mathematical signs to each current, indicating their direction (+ for entering, - for exiting), we can solve for the unknown value.
KCL is a powerful tool for analysing parallel circuits, as it allows us to balance the currents at each node and ensure that the conservation of charge is satisfied. By applying KCL to each node in a complex circuit, we can gain insights into the distribution of currents and validate the behaviour of the circuit.
Leash Laws: Do Cats Need to Follow Them?
You may want to see also

KCL can be used to solve for unknown currents in a circuit
Kirchhoff's Current Law (KCL) is a powerful tool for understanding and analysing the flow of current in electrical circuits. It is based on the principle of charge conservation, stating that the total current entering a junction equals the total current leaving the junction. In other words, the sum of currents entering the junction is exactly equal to the sum of currents flowing out. This can be expressed by the equation:
\[ \displaystyle\sum_{k=1}^{n} I_k=0\]
Where:
- ∑ represents the summation, indicating that all currents entering and leaving the junction must be added together.
- K is an index used to reference each individual current entering or leaving the junction.
- N is the total number of currents flowing into or out of the junction.
- Ik represents the current of the kth path. Currents entering are considered positive, while currents leaving are considered negative.
- Identify and label the direction of currents with respect to the node.
- Apply KCL by summing the currents entering and leaving the node, setting the equation to equal zero.
- Solve for the unknown current by rearranging the equation.
For example, consider a circuit node where three branches converge. Branch 1 has a current I1 flowing towards the node, branch 2 has a current I2 flowing away from the node, and branch 3 has an unknown current I3 flowing towards the node. By applying KCL and substituting the known values, we get:
\+I1\−I2\+I3=0
Rearranging the equation, we find that I3=3A−2A, which gives us the unknown current I3 flowing towards the node as 1A.
KCL can also be applied to more complex circuits involving resistors and power sources by incorporating Ohm's Law (V=IR). First, apply KCL to each node in the circuit, setting up equations based on the current flowing into and out of the nodes. Then, apply Ohm's Law to express the voltages in terms of current and resistance. Finally, solve the resulting system of equations to find the unknown currents.
KCL is a fundamental principle in circuit analysis, but it has certain limitations. It assumes a steady-state condition, implying no charge accumulation at any node over time. It also assumes ideal conductors and no time-varying electromagnetic fields within the circuit. In scenarios with changing magnetic fields, high-frequency AC circuits, or quantum/nano-scale circuits, KCL might not directly apply due to non-conservative electric fields or transient behaviours.
Employment Laws: Contractors' Rights and Legal Protections
You may want to see also

KCL simplifies complex circuits and makes unknown voltage and current calculations easier
Kirchhoff's Current Law (KCL) is a powerful tool for simplifying complex circuits and facilitating calculations of unknown voltages and currents. KCL is based on the principle of conservation of charge, stating that the total current entering a node equals the total current leaving it. This law enables us to analyse intricate circuits with multiple paths and junctions, making it an essential technique for electronics engineers and designers working with complex circuitry.
When dealing with complex circuits, KCL simplifies the process of identifying unknown currents and voltages. By applying KCL, we can set up a system of linear equations that relates the known and unknown values in the circuit. This systematic approach ensures that all relevant factors are considered, reducing the chances of error and simplifying the circuit analysis process.
To illustrate the application of KCL, let's consider a complex circuit with multiple branches and junctions. We can start by labelling each branch with a unique current label, such as I1, I2, and so on. Next, we identify the nodes or junctions where three or more wires connect. At each node, we apply KCL, stating that the sum of incoming currents equals the sum of outgoing currents. This results in a set of equations that represent the current flow at each node.
Additionally, KCL can be combined with Kirchhoff's Voltage Law (KVL) to further simplify complex circuits. KVL states that the sum of voltage drops around any closed loop in a circuit is zero. By applying both KCL and KVL, we can create a comprehensive set of equations that describe the circuit's behaviour. This combination of laws allows us to analyse circuits with multiple loops and interconnected components effectively.
For instance, consider a circuit with two voltage sources, V1 and V2, and multiple resistors. By applying KCL at the junctions and KVL to the loops, we can establish equations that relate the currents and voltages in the circuit. Solving these equations will provide us with the unknown current and voltage values, enabling a comprehensive understanding of the circuit's behaviour.
In conclusion, KCL is a valuable tool for simplifying complex circuits and facilitating voltage and current calculations. By applying KCL, we can set up a system of equations that relates the known and unknown values, making it easier to analyse intricate circuits with multiple paths and junctions. When combined with KVL, KCL becomes an even more powerful tool for circuit analysis, providing a systematic approach to understanding and designing complex electrical systems.
Understanding Romeo and Juliet Laws: Applicability for 21-Year-Olds
You may want to see also

KCL is based on the principle of conservation of charge
Kirchhoff's Current Law (KCL) is a fundamental principle in electrical engineering that plays a crucial role in understanding and analysing complex circuits. This law is firmly rooted in the principle of conservation of charge, which asserts that the total charge entering a system must be equal to the total charge leaving it. In the context of electrical circuits, this translates to the idea that the current flowing into a node or junction must be equal to the current flowing out.
KCL, also known as the junction rule, essentially states that the algebraic sum of currents meeting at a junction is zero. In mathematical terms, this can be expressed as Σ i = 0. This means that at any given junction within a circuit, the sum of currents flowing into that junction must be equal to the sum of currents exiting it. For example, if we consider the currents i1, i2, i3, and i4, KCL dictates that i1 + i3 = i2 + i4. This equation underscores the fundamental principle of conservation of charge.
The significance of KCL lies in its ability to ensure charge conservation within a circuit. If the current entering a junction is not equal to the current leaving it, charge would not be conserved, leading to an accumulation or depletion of charge at the junction. KCL prevents this by requiring that the sum of currents at the junction be zero, ensuring a dynamic equilibrium where incoming charges pass through the junction without net accumulation.
Kirchhoff's laws, which include KCL and Kirchhoff's Voltage Law (KVL), provide powerful tools for analysing complex circuits. While Ohm's Law is sufficient for simpler circuits, KCL and KVL come into play when dealing with more intricate arrangements, such as those with bridges or T networks. By applying KCL, engineers can validate the current flow within a circuit, ensuring that the conservation of charge principle is upheld.
Duverger's Law and Its Application in France
You may want to see also







