What Law Applies To Triangles: A Comprehensive Guide

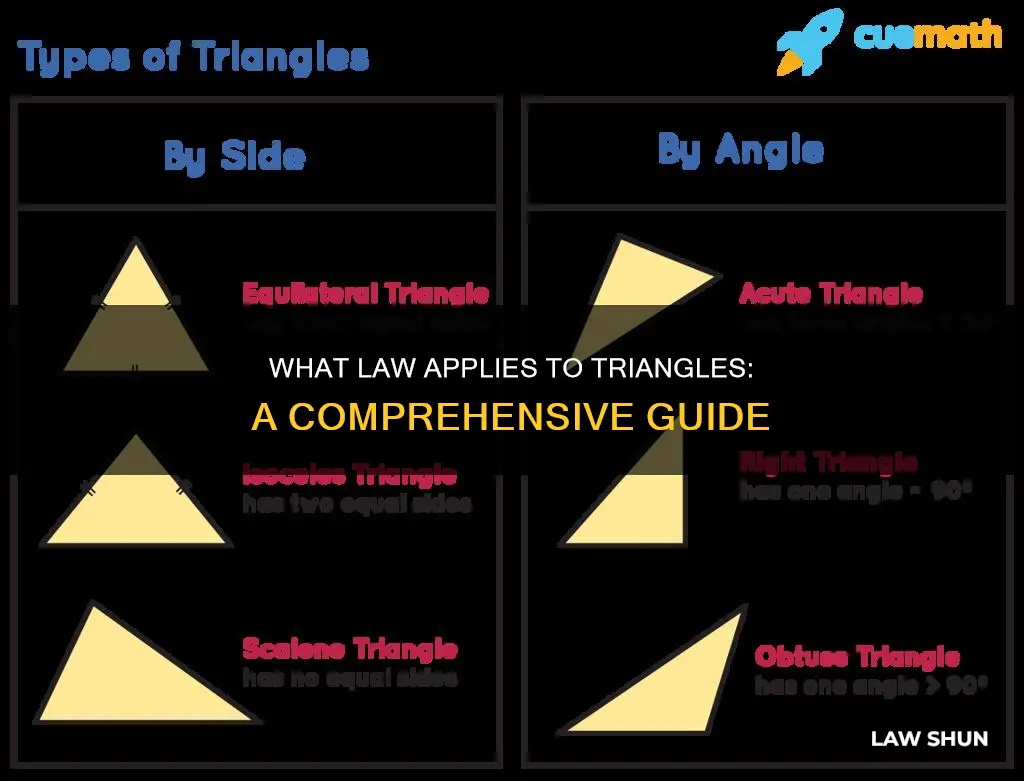
Triangles are one of the most fundamental shapes in geometry and have a variety of properties. One of the most well-known rules about triangles is that the sum of all three interior angles is always 180°. There are several laws that apply to triangles, such as the Law of Sines (or Sine Rule) and the Law of Cosines, which can be used to solve for unknown sides or angles in a triangle. The Law of Sines states that the ratio of the sides of a triangle is equal to the ratio of the sines of the angles opposite those sides. The Law of Cosines, on the other hand, is used to find unknown sides or angles in scalene triangles. Triangles can also be classified in two major ways: according to their internal angles and according to the length of their sides.

The Law of Sines

A/sin A = b/sin B = c/sin C

This law can be used to find unknown sides or angles in a triangle. For example, if we know the values of two sides and one angle, we can use the Law of Sines to find the other angle. Similarly, if we know the values of two angles and one side, we can use the law to find the third angle.

The Triangle Inequality Theorem

This theorem can be expressed mathematically as:

A + b > c, b + c > a, and c + a > b, where a, b, and c represent the lengths of the sides of a triangle.

For example, let's consider the following side lengths: 4 cm, 8 cm, and 2 cm. By applying the Triangle Inequality Theorem, we can determine if a triangle can be formed:

4 cm + 8 cm > 2 cm: True

8 cm + 2 cm > 4 cm: True

4 cm + 2 cm > 8 cm: False

Since one of the conditions does not satisfy the theorem, we conclude that a triangle cannot be formed with these side lengths.

The Triangle's Interior Angles

The interior angles of a triangle are the angles inside the triangle. There are three interior angles in a triangle, and the sum of these angles is always 180° or π radians. This is known as the Triangle Angle Sum Theorem.

The interior angles of a triangle are bounded by a pair of adjacent edges. The largest interior angle is opposite the largest side, the smallest interior angle is opposite the smallest side, and the middle-sized interior angle is opposite the middle-sized side.

The sum of the interior angles of a triangle in Euclidean space is always 180°. This fact is equivalent to Euclid's parallel postulate, which allows us to determine the measure of the third angle of any triangle when given the measure of two angles.

The interior angles of a triangle can be used to find missing angles inside the triangle. For example, if we are given that angle A = 15° and angle C = 92° in a triangle, we can use the Triangle Angle Sum Theorem to find the measure of the third angle, B.

B = 180° - A - C

B = 180° - 15° - 92°

B = 73°

Therefore, the three interior angles of the triangle are 15°, 73°, and 92°.

The Triangle's Exterior Angles

The exterior angles of a triangle are the angles formed outside it. In other words, an exterior angle is formed between one side of the triangle and the extension of an adjacent side. Each exterior angle forms a linear pair with its corresponding interior angle, meaning the sum of each exterior angle and its respective interior angle is 180°.

There are three exterior angles in a triangle, and each vertex has two exterior angles. The sum of all the exterior angles of a triangle is 360°.

The exterior angle of a triangle is equal to the sum of the two opposite interior angles (also known as the remote interior angles). This is also known as the Exterior Angle theorem.

• If one interior angle of a triangle is 56°, its corresponding exterior angle is 180° - 56° = 124°.
• If the exterior angle, ∠PRS = 60° and ∠PQR = 70°, then the unknown exterior angle, ∠PRS = 60° + 70° = 130°.

The Triangle's Sides

The triangle is a fundamental geometric shape with three sides and three angles, each angle being bounded by a pair of adjacent sides. The sum of the angles of a triangle is always 180 degrees or π radians.

The sides of a triangle are one-dimensional line segments that connect the corners or vertices. The sides are also called edges. Sometimes, an arbitrary side is chosen to be the base, in which case the opposite vertex is called the apex, and the shortest distance between the base and apex is the height. The area of a triangle is half the product of the height and the base length.

There are several laws and rules that relate to the sides of a triangle. The Triangle Inequality Theorem states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side. The largest interior angle and side are opposite each other, with the same rule applying to the smallest and middle-sized angles and sides.

The Law of Sines, or Sine Rule, is a trigonometric equation that can be used to find unknown sides and angles in any triangle. It states that:

> a/sin A = b/sin B = c/sin C = 2R

Where a, b, and c are the lengths of the sides, and A, B, and C are the angles opposite those sides, and R is the radius of the triangle's circumcircle.

The Law of Sines can be used when two angles and a side are known, or when two sides and one non-enclosed angle are known. In some cases, this may result in two possible values for the enclosed angle, as two separate triangles can be constructed from the data.

The Law of Cosines is another trigonometric equation that can be used to find unknown sides and angles in a triangle.

Frequently asked questions