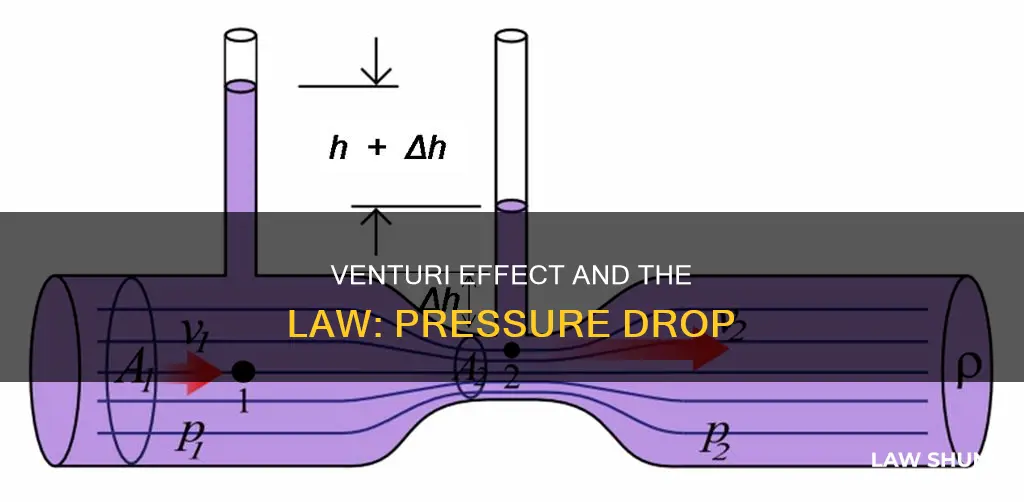
The Venturi effect is a principle in fluid dynamics that explains the decrease in fluid pressure as it flows through a constricted section of a pipe. This phenomenon is named after 18th-century Italian physicist Giovanni Battista Venturi, who discovered that when a fluid moves through a narrower section of a pipe, its velocity increases while its static pressure decreases. The Venturi effect is not limited to fluids in pipes but can also be observed in everyday situations, such as the wind blowing stronger between skyscrapers or the suction created by placing your thumb over a garden hose. Bernoulli's principle, based on the conservation of energy, helps explain this effect by demonstrating that an increase in kinetic energy leads to a decrease in potential energy or static pressure. This relationship between pressure and velocity is essential for understanding process control and the safe operation of industrial plants, as well as for designing aircraft wings and natural ventilation systems.
| Characteristics | Values |
|---|---|
| Name | Venturi effect |
| Discovery | Named after 18th-century Italian physicist Giovanni Battista Venturi |
| Definition | Drop in static pressure of a fluid as it flows through a constricted area of a pipe |
| Formula | \(p_1 – p_2 = \frac{\rho}{2} (v_2^2 – v_1^2)\) |
| Variables | p = pressure, \(\rho\) = fluid density, v = velocity |
| Principle | Bernoulli's principle |
| Applications | Measuring fluid flow, moving other fluids, flow measurement devices, mixing liquid and gas components |
What You'll Learn

Bernoulli's principle
$p_1 - p_2 = \frac{\rho}{2} (v_2^2 - v_1^2)$
Where:
- $p_1$ and $p_2$ represent the pressures at two different points in the fluid, with $p_1$ being the pressure in the wider section and $p_2$ the pressure in the narrower section
- $\rho$ is the density of the fluid
- $v_1$ and $v_2$ are the fluid velocities at the respective points
The Bernoulli equation shows that when there is a pressure drop ($p_1 - p_2$), the velocity of the fluid increases ($v_2^2 - v_1^2$), and vice versa. This relationship is essential for understanding and designing various engineering applications, such as flow measurement devices and fluid transport systems.
By utilising Bernoulli's principle and the Venturi effect, engineers can design more efficient systems and optimise processes. For example, in industrial and scientific settings, Venturi tubes are commonly used to measure the flow rate of fluids by attaching manometers to measure pressure differences, which can then be used to calculate flow rates. Additionally, Venturi tubes can be used to mix liquid and gas components by taking advantage of the pressure difference created within the tube.
Black Holes: Beyond the Laws of Physics?
You may want to see also

The principle of conservation of energy
The Venturi effect is named after 18th-century Italian physicist Giovanni Battista Venturi. It is defined as the drop in static pressure of a fluid as it flows through a narrower section of a pipe, resulting in an increase in velocity. This phenomenon is described by Bernoulli's principle, which is based on the principle of conservation of energy. Bernoulli's principle states that in a steady, streamlined flow, the sum of all forms of energy (kinetic, potential, and internal) remains constant at all points.
In the context of the Venturi effect, as the fluid's velocity increases, its potential energy decreases, leading to a drop in pressure. This relationship between velocity and pressure can be expressed mathematically using the Bernoulli equation:
> p1 – p2 = (ρ/2) * (v2^2 – v1^2)
Where:
- P1 and p2 represent the pressure at two different points in the pipe
- Ρ is the density of the fluid
- V1 and v2 are the fluid velocities at the wider and narrower sections of the pipe, respectively
This equation demonstrates that an increase in velocity leads to a decrease in pressure, and vice versa. The conservation of energy is evident in this equation, as the total energy of the fluid remains constant, even as its form changes.
The Venturi effect has various engineering applications and is utilized in everyday machines such as vacuum cleaners, ventilators, and automobile diffusers. It is also employed in flow measurement devices like Venturi meters and nozzles, where the change in pressure is used to determine the flow rate.
Airplane Laws: Jurisdiction in the Skies
You may want to see also

The principle of mass continuity
This principle is essential for comprehending the Venturi effect, which is defined as the reduction in fluid pressure that occurs when a moving fluid speeds up as it flows through a constricted section of a pipe. The Venturi effect was named after 18th-century Italian physicist Giovanni Battista Venturi, who discovered it.
The Venturi effect and the principle of mass continuity have significant engineering applications. By understanding how fluid velocity and pressure change in a constricted section of a pipe, engineers can design and optimise systems that rely on these principles. For example, in heat sink design, large posts and fins are used to constrict airflow and enhance heat transfer into a nearby flowing fluid.
Additionally, the principle of mass continuity is essential for flow rate calculations. By measuring the change in pressure using devices such as Venturi meters, engineers can determine the flow rate of fluids. This is particularly useful in industrial applications and scientific laboratories for measuring the flow rate of liquids.
Applying to the University of Law: A Step-by-Step Guide
You may want to see also

The principle of conservation of mechanical energy
This principle is based on the law of conservation of energy, which states that energy cannot be created or destroyed, only transferred or transformed. In the case of mechanical energy, this means that the total amount of mechanical energy in a system stays the same unless non-conservative forces, such as friction, act upon it.
The Venturi effect, which is the decrease in fluid pressure as it passes through a constriction, can be explained by the principle of conservation of mechanical energy. As the fluid flows through a narrower section of a pipe, its velocity increases, leading to a decrease in pressure. This relationship between velocity and pressure is described by Bernoulli's principle, which states that any gain in kinetic energy due to increased velocity is balanced by a drop in pressure due to a loss in potential energy.
The Venturi effect is not limited to fluids; it can also be observed in gases. For example, when you place your thumb over the end of a garden hose, the water's velocity increases, creating a decrease in cross-sectional area. As a result, the pressure increases over a smaller surface area, and the fluid's kinetic energy increases, resulting in a pressure decrease.
Applying for Temporary Lawful Residency in the USA
You may want to see also

The principle of conservation of momentum
The Venturi effect is a phenomenon observed in fluid dynamics, where the pressure of a fluid flowing through a pipe decreases as it passes through a constricted section. This effect is named after the 18th-century Italian physicist Giovanni Battista Venturi, who discovered it.
The Venturi effect is based on the principle of conservation of momentum, which is related to the conservation of mass and energy. When a fluid flows through a narrower section of a pipe, it must increase its velocity to ensure that the mass flow rate remains constant, as per the continuity condition in the Navier-Stokes equation. This increase in velocity is facilitated by a decrease in pressure, demonstrating the conservation of momentum.
The Bernoulli equation, which describes the relationship between velocity and pressure, can be used to explain the Venturi effect:
P_1 – p_2 = (1/2) * rho * (v_2^2 – v_1^2)
Where:
- P_1 and p_2 are the pressures at two different points in the pipe
- Rho is the fluid density
- V_1 and v_2 are the fluid velocities at the same points
This equation shows that when there is a pressure drop (p_1 – p_2), the velocity of the fluid increases (v_2^2 – v_1^2). This relationship is essential in understanding the Venturi effect, as it illustrates the trade-off between pressure and velocity.
The Venturi effect has numerous applications in engineering, particularly in measuring fluid flow and moving other fluids. Devices such as Venturi meters, nozzles, and orifice plates utilise the Venturi effect to determine flow rates by measuring pressure differences. Additionally, the Venturi effect is used in vacuum ejectors, fuel injectors, jet pumps, and carburettors, among other applications.
Obtaining a Law License in Texas: A Guide
You may want to see also
Frequently asked questions
The Venturi effect is the reduction in fluid pressure that results when a moving fluid speeds up as it flows through a constricted section (or choke) of a pipe.
Bernoulli's principle states that within a specified flow field, a decrease in pressure occurs when there is an increase in velocity. Bernoulli's principle is based on the principle of conservation of energy, according to which, in a steady, streamlined flow, the sum of all energy (kinetic, potential, and internal energy) should remain constant at all points.
The Venturi effect has various engineering applications, as the reduction in pressure inside the constriction can be used both for measuring the fluid flow and for moving other fluids (e.g. in a vacuum ejector). Venturi tubes are often used in industrial and scientific fields to measure the flow rate of a fluid.