Kirchhoff's circuit laws are two equalities that deal with the current and voltage in electrical circuits. They were first described in 1845 by German physicist Gustav Kirchhoff and are widely used in electrical engineering. The laws can be applied to both AC and DC circuits, and they form the basis for network analysis. Kirchhoff's current law, or his first law, states that the sum of currents flowing into a node is equal to the sum of currents flowing out of that node. Kirchhoff's voltage law, or his second law, states that the directed sum of potential differences (voltages) around any closed loop is zero. These laws can be used to calculate the currents and voltages in a circuit and are particularly useful for complex circuits where Ohm's Law alone is insufficient.
| Characteristics | Values |
|---|---|
| What are Kirchhoff's Laws? | Two equalities that deal with the current and potential difference (commonly known as voltage) in the lumped element model of electrical circuits. |
| When were Kirchhoff's Laws first described? | 1845 |
| Who described Kirchhoff's Laws? | German physicist Gustav Kirchhoff |
| What do Kirchhoff's Laws generalize? | The work of Georg Ohm |
| What did Kirchhoff's Laws precede? | The work of James Clerk Maxwell |
| When are Kirchhoff's Laws accurate? | For DC circuits, and for AC circuits at frequencies where the wavelengths of electromagnetic radiation are very large compared to the circuits. |
| What is another name for Kirchhoff's Current Law? | Kirchhoff's First Law or Kirchhoff's Junction Rule |
| What does Kirchhoff's Current Law state? | The sum of the currents flowing into a node is equal to the sum of currents flowing out of that node. |
| What is another name for Kirchhoff's Voltage Law? | Kirchhoff's Second Law or Kirchhoff's Loop Rule |
| What does Kirchhoff's Voltage Law state? | The directed sum of the potential differences (voltages) around any closed loop is zero. |
What You'll Learn

Kirchhoff's First Law – The Current Law, (KCL)
Kirchhoff's Current Law, also known as Kirchhoff's First Law or KCL, is a fundamental principle in circuit analysis. Gustav Kirchhoff, a German physicist, formulated this law in 1845 as part of his work on the conduction of electricity.
KCL states that the total current entering a junction or node in a circuit is equal to the total current leaving that same junction. In other words, no charge is lost at a node, and the algebraic sum of all currents entering and exiting a node is always zero. This principle is often referred to as the Conservation of Charge.
Mathematically, KCL can be expressed as:
I(exiting) + I(entering) = 0
Or:
Σ I_IN = Σ I_OUT
This law is particularly useful when analysing parallel circuits and complex circuits with multiple junctions or nodes. By applying KCL, we can determine the magnitude of currents at each node and ensure that the conservation of charge is satisfied.
For example, consider a simple parallel resistor circuit with two distinct junctions, at nodes B and E. At node B, the current can flow in two directions: downwards through resistor R1 or continue through resistor R2 via node C. Using KCL, we can calculate the sum of currents entering and leaving node B. This calculation helps verify that Kirchhoff's Junction Rule, or KCL, holds true for this circuit.
KCL is a powerful tool for understanding and analysing electrical circuits, and it forms the basis for more complex circuit analysis techniques.
The Ever-Relevant Moses Law: Still Applicable Today?
You may want to see also

Kirchhoff's Second Law – The Voltage Law, (KVL)
Kirchhoff's Second Law, also known as Kirchhoff's Voltage Law (KVL), is a fundamental concept in electrical circuit theory. KVL is one of the two laws formulated by German physicist Gustav Kirchhoff in 1845 as part of his doctoral dissertation. The law deals with the conservation of energy within electrical circuits and provides a powerful tool for analysing complex circuits.
Kirchhoff's Voltage Law states that in any closed-loop network driven by a voltage source, the total voltage around the loop is equal to the sum of all the voltage drops within the same loop, which is equal to zero. In other words, the algebraic sum of all voltage sources and voltage drops within a closed loop must be equal to zero. This is based on the principle of conservation of energy, which states that the net change in energy of a charge after completing a closed loop must be zero.
To apply Kirchhoff's Voltage Law, one must follow a consistent direction, either clockwise or anticlockwise, around the loop. The direction of current flow and the polarity of voltage drops are crucial for accurate calculations. Voltage drops across components are considered negative when the looping direction is the same as the current flow. By accounting for all voltage drops and gains and maintaining a consistent direction, the final voltage sum will be zero.
The law is particularly useful for analysing series circuits and calculating unknown voltages and currents in complex closed-loop circuits. It is important to note that Kirchhoff's laws assume the absence of fluctuating magnetic fields, as their presence could induce electromotive forces and violate the laws.
Men's Legal Responsibilities: Unique Laws for Men?
You may want to see also

Kirchhoff's Current Law and Ohm's Law
Kirchhoff's Current Law (KCL) and Ohm's Law are fundamental concepts in understanding the behaviour of electrical circuits.
Kirchhoff's Current Law:
Gustav Kirchhoff, a German physicist, formulated a set of rules, now known as Kirchhoff's Circuit Laws, in 1845. These laws deal with the conservation of current and energy within electrical circuits. KCL states that the "total current or charge entering a junction or node is exactly equal to the charge leaving the node as it has no other place to go except to leave, as no charge is lost within the node." Mathematically, this can be expressed as I(exiting) + I(entering) = 0, or in other words, the algebraic sum of all currents entering and leaving a node must be equal to zero. This principle is based on the idea of charge conservation.
Ohm's Law:
Ohm's Law, formulated by German physicist Georg Ohm and published in 1827, characterises the relationship between voltage, current, and resistance in an electrical circuit. It is expressed by the equation: V = IR, where V is voltage, I is current, and R is resistance. This law reveals that electric current flowing through a conductor between two points is directly proportional to the voltage across those points, with resistance serving as the constant of proportionality.
Application in DC Circuits:
In DC circuits, Ohm's Law can be used to calculate voltage, current, or resistance. For instance, if voltage (V) and current (I) are known, resistance (R) can be calculated by rearranging Ohm's Law to give R = V/I. Similarly, if voltage (V) and resistance (R) are known, current (I) can be found using I = V/R. These calculations are particularly useful when a circuit is operational, as resistance cannot be measured directly in such cases.
Castle Law: Children's Rights and Protections Explored
You may want to see also

Kirchhoff's Voltage Law and Capacitors
Kirchhoff's Circuit Laws, developed by German physicist Gustav Kirchhoff in 1845, are a set of rules that deal with the conservation of current and energy within electrical circuits. They allow us to solve complex circuit problems by defining a set of basic network laws and theorems for voltages and currents.
Kirchhoff's Voltage Law (KVL) is one of these two laws and it states that "in any closed-loop network being driven by a voltage source, the total voltage around the loop is equal to the sum of all the voltage drops within the same loop", which is equal to zero. In other words, the algebraic sum of all voltage sources and voltage drops within a closed loop must be equal to zero as the algebraic sum of the voltage drops equals the algebraic sum of the voltage sources. This principle is known as the Conservation of Energy.
When applying Kirchhoff's Voltage Law, it is important to maintain the same direction, either clockwise or anticlockwise, when noting the direction of all the voltage drops, otherwise, the final voltage sum will not be equal to zero. This law can be used when analysing series circuits.
Kirchhoff's Voltage Law can be applied to circuits with capacitors. Kirchhoff's rules can be used to determine the potential difference and charge on the plates of a capacitor in any electric circuit. A capacitor circuit obeys the principle of conservation of charge, which is the Junction Rule. This rule states that the incoming charge at any junction is equal to the outgoing charge from the junction, i.e. q = q1 + q2, or in other words, in any isolated system, the net charge is conserved.
Ohm's Law: Powering Our Daily Lives
You may want to see also

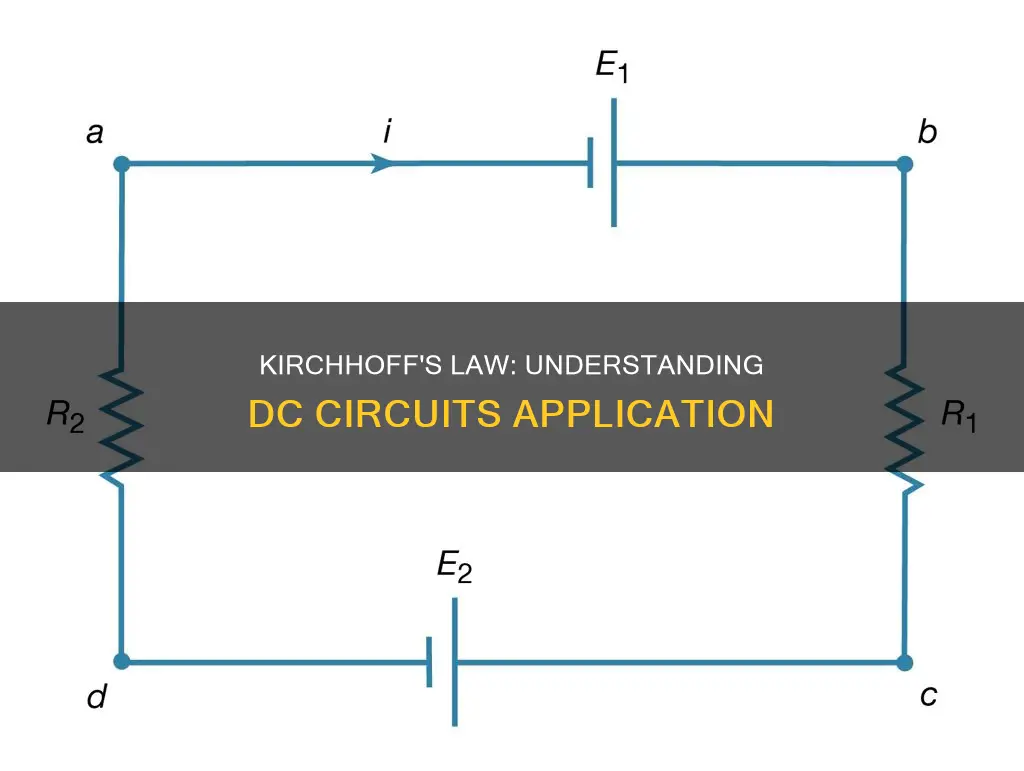
Kirchhoff's Law and DC Circuit Theory
Kirchhoff's Circuit Laws are fundamental to understanding and analysing electrical circuits. They were formulated by German physicist Gustav Kirchhoff in 1845, building on the work of Georg Ohm and preceding that of James Clerk Maxwell. These laws are widely used in electrical engineering and form the basis for network analysis.
Kirchhoff's laws consist of two equalities that deal with the current and voltage in the lumped element model of electrical circuits. They are accurate for DC circuits and can be applied in both time and frequency domains. The laws are derived from experimental results and are applicable to any lumped network, irrespective of its nature.
Kirchhoff's Current Law (KCL)
Kirchhoff's Current Law, also known as Kirchhoff's First Law or Kirchhoff's Junction Rule, states that the total current entering a junction or node is equal to the total current leaving that node. In other words, the algebraic sum of all currents entering and leaving a node is equal to zero (I(exiting) + I(entering) = 0). This principle is based on the conservation of charge, where no charge is lost within the node.
Kirchhoff's Voltage Law (KVL)
Kirchhoff's Voltage Law, also known as Kirchhoff's Second Law or Kirchhoff's Loop Rule, states that the sum of the voltages around any closed loop in a circuit is equal to zero. This is based on the conservation of energy, where the algebraic sum of all voltage sources and drops within a closed loop must be equal to zero.
Application to DC Circuits
When analysing DC circuits using Kirchhoff's laws, it is important to understand the definitions and terminologies used to describe the circuit components. Common terms include:
- Circuit: A closed-loop conducting path in which an electrical current flows.
- Path: A single line of connecting elements or sources.
- Node: A junction, connection, or terminal within a circuit where two or more elements are joined, indicated by a dot.
- Branch: A single or group of components connected between two nodes.
- Loop: A simple closed path in a circuit where no element or node is encountered more than once.
- Mesh: A single closed-loop series path that does not contain any other paths.
Kirchhoff's laws can be used to calculate voltages and currents in a DC circuit. By applying these laws to each node and loop in the circuit, a set of simultaneous equations can be derived, which can then be solved to find the unknown currents and voltages.
In summary, Kirchhoff's Circuit Laws provide a powerful tool for analysing DC circuits, allowing us to solve complex problems and calculate voltages and currents within the circuit. These laws are based on the conservation of charge and energy and are widely applied in electrical engineering.
Service Animal Laws: Contractor Compliance Explored
You may want to see also
Frequently asked questions
Kirchhoff's laws are two equalities that deal with the current and potential difference (commonly known as voltage) in the lumped element model of electrical circuits. They were formulated by German physicist Gustav Kirchhoff in 1845.
Kirchhoff's First Law, also known as Kirchhoff's Current Law, states that the total current entering a junction or node is equal to the charge leaving the node, as no charge is lost. In other words, the sum of the currents flowing into a node is equal to the sum of currents flowing out of that node.
Kirchhoff's Second Law, also known as Kirchhoff's Voltage Law, states that the sum of the voltages around any closed loop in a circuit is equal to zero.







