Kepler's Laws: Binary Star Motions Explained

Kepler's Third Law is the last of the revolutionary theorems by German astronomer Johannes Kepler, which explains planetary orbits around the sun. The law states that the orbit of a planet is an ellipse with the sun at one of the two foci. Kepler's third law can be used to calculate the masses of stars in binary systems, which is vital to understanding the structure and evolution of stars. The binary mass function is derived from Kepler's third law and the fact that bodies orbit a mutual center of gravity.

Kepler's Third Law and binary star motions

Kepler's Third Law, also known as The Law of Harmony, was the last of the revolutionary theorems by German astronomer and mathematician Johannes Kepler. Kepler's Third Law describes the motion of two bodies orbiting a common centre of mass. It relates the orbital period with the orbital separation between the two bodies and the sum of their masses.

The law can be used to calculate the masses of the bodies involved in the system described. Given mass 1 (m1) and mass 2 (m2), the masses of the two bodies, m1 describing the star is usually so significantly larger than m2 that the mass of the orbiting body can be ignored.

Kepler's Third Law can be applied to binary star motions. In this case, the binary mass function is derived from Kepler's third law and the fact that bodies orbit a mutual centre of gravity. When considering stars and planets, this is much closer to the star because of the planet's much smaller mass. For binary stars, astronomers can calculate the sum of the masses of the two stars if they know the period of the stars and their average separation.

The equation for Kepler's Third Law is P² = a³, so the period of a planet's orbit (P) squared is equal to the size of the semi-major axis of the orbit (a) cubed when expressed in astronomical units.

Kepler's Third Law can be used to calculate the masses of planets in our solar system, with accurate masses and mean densities found for Mars, Jupiter, and Saturn. It can also be applied to planets and their moons and even artificial satellites placed in orbit around them.

Calculating the mass of a binary star system

Binary star systems are important to astronomers as they provide a means of directly determining the masses of stars other than our Sun. This is vital in refining our models of stars as mass is such a key property of stars.

Kepler's Laws

The German astronomer Johannes Kepler (1571–1630) devised a set of three laws, called Kepler's laws of planetary motion, that describe the orbits of all bodies satisfying two conditions:

• The mass of the orbiting object, m, is small compared to the mass of the object it orbits, M.
• The system is isolated from other massive objects.

Kepler's Third Law states that the ratio of the squares of the periods of any two planets around a central body is equal to the ratio of the cubes of their average distances from that body.

The mass of a binary star system can be calculated from measurements of their orbits, just as the mass of the Sun can be derived by measuring the orbits of the planets around it. The mass of a binary system can be deduced from Kepler's Third Law. The total mass of a binary system can be found from the relation M1 + M2 = a^3/P^2, where a is the orbital separation of the two bodies and P is the orbital period.

However, it is harder to determine the individual masses of the component stars. This requires the distance from a component star to the barycenter (the centre of mass of the system) to be measured as well. The distance of the two stars from the barycenter is given by the relation M1/M2 = a2/a1, where a1 = distance of the first star from the barycenter, and a2 = distance of the second star from the barycenter.

To summarise, a good measurement of the motion of two stars around a common centre of mass, combined with the laws of gravity, allows us to determine the masses of stars in such systems.

The binary mass function

In astronomy, the binary mass function is a function that determines the mass of the unseen component (usually a star or exoplanet) in a single-lined spectroscopic binary star or in a planetary system. It is calculated using only observable quantities, namely the orbital period of the binary system and the peak radial velocity of the observed star.

The true mass and true orbital velocity of a binary system cannot be determined solely from radial velocity measurements. This is because the orbital inclination, or the angle of the orbit from the observer's perspective, is typically unknown. This uncertainty leads to a degeneracy between mass and inclination. For example, a low measured radial velocity could indicate either low-mass objects with a high inclination (edge-on orbit) or high-mass objects with a low inclination (face-on orbit).

To address this challenge, astronomers use additional techniques such as observing eclipses, modelling ellipsoidal variations, or making assumptions about the mass of the observed object. By combining these approaches with the binary mass function, astronomers can estimate the minimum mass of the unseen companion.

Eccentricity and elliptical orbits

Eccentricity is a measure of how elliptical an orbit is. In the case of binary star systems, the two stars orbit a common centre of mass, also known as the barycentre, and their orbits are elliptical. These elliptical orbits can vary from almost circular to highly elliptical. The eccentricity of an elliptical orbit is calculated by dividing the distance from the centre of the ellipse to one of the foci by half the length of the long axis. This value, denoted as 'e', is always less than 1. If e is close to 0, the orbit is more circular, and as e increases towards 1, the orbit becomes more elliptical.

In binary star systems, the two stars' elliptical orbits share a common focus at the barycentre. The radius vector joining the two stars always passes through the barycentre. The distances between each star and the barycentre change over time, but the stars never collide as they are always on opposite sides of the centre of mass. The semi-major axis of an ellipse is one-half of its long axis, and in the case of binary star systems, each star's orbit has its own semi-major axis, denoted as 'a1' and 'a2' for the two stars, respectively.

The concept of eccentricity is closely tied to Kepler's laws of planetary motion, specifically the first and third laws. Kepler's first law states that the orbit of each planet around the sun is an ellipse with the sun at one focus. This law can be applied to binary star systems, where each star orbits the common centre of mass in an elliptical path. Kepler's third law describes the motion of two bodies orbiting a common centre of mass and relates the orbital period and the orbital separation between the two bodies to the sum of their masses. This law is particularly useful in binary star systems, as it allows astronomers to determine the masses of the stars by measuring the orbital period and separation.

In summary, eccentricity plays a crucial role in understanding the elliptical orbits of binary star systems. The orbits of the stars can vary in their ellipticity, with eccentricity values closer to 0 being more circular and values closer to 1 being more elliptical. Kepler's laws, particularly the first and third laws, provide a framework for understanding the elliptical nature of these orbits and enable astronomers to calculate important characteristics of the system, such as the masses of the stars.

Kepler's Laws and the Copernican revolution

The Copernican Revolution refers to the paradigm shift from the geocentric model of the universe, with Earth at its centre, to the heliocentric model, with the Sun at the centre of the Solar System. This revolution is named after Nicolaus Copernicus, who first presented the heliocentric model in his Commentariolus, written before 1514. However, the idea of heliocentrism is much older, dating back to the 3rd century BC with the Hellenistic author, Aristarchus of Samos.

Despite the Copernican Revolution, ancient ideas about the universe persisted. Philosophers and astronomers, including Copernicus himself, continued to believe that the planets followed circular orbits. This belief was rooted in the idea that the circle was the universe's perfect shape, a manifestation of divine order. It was not until Johannes Kepler, working with Tycho Brahe's extensive astronomical observations, discovered that the planets followed elliptical orbits.

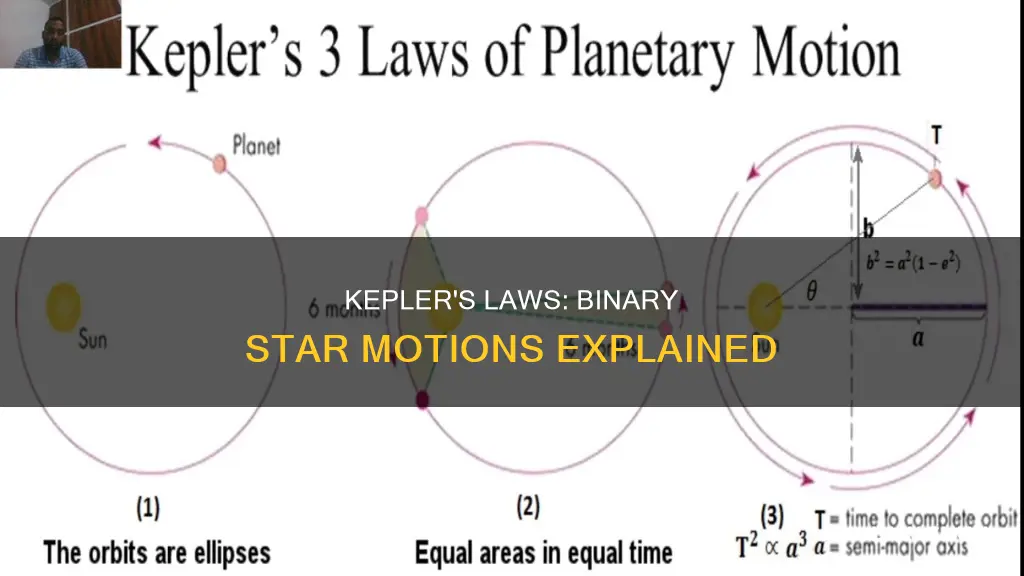
Kepler's three laws of planetary motion were:

• The Law of Ellipses: All planets move in elliptical orbits, with the Sun at one focus.
• The Law of Equal Areas in Equal Time: A line that connects a planet to the Sun sweeps out equal areas in equal times.
• The Law of Harmony: The time required for a planet to orbit the Sun, called its period, is proportional to the long axis of the ellipse raised to the 3/2 power. The constant of proportionality is the same for all the planets.

Kepler's laws were purely descriptive and did not provide any causal explanation for the patterns he observed. However, they marked a significant advancement in our understanding of the cosmos and set the stage for later astronomers like Galileo Galilei and Isaac Newton to build upon. Newton, in particular, used Kepler's laws to derive his law of universal gravitation, which explained the gravitational force of attraction between two objects.

Frequently asked questions