The law of cosines, also known as the cosine formula or cosine rule, relates the lengths of the sides of a triangle to the cosine of one of its angles. The law of cosines can be used to find the third side of a triangle when we know two sides and the angle between them, or the angles of a triangle when we know all three sides. The formula for the law of cosines is:
c^2 = a^2 + b^2 - 2ab cos(C)
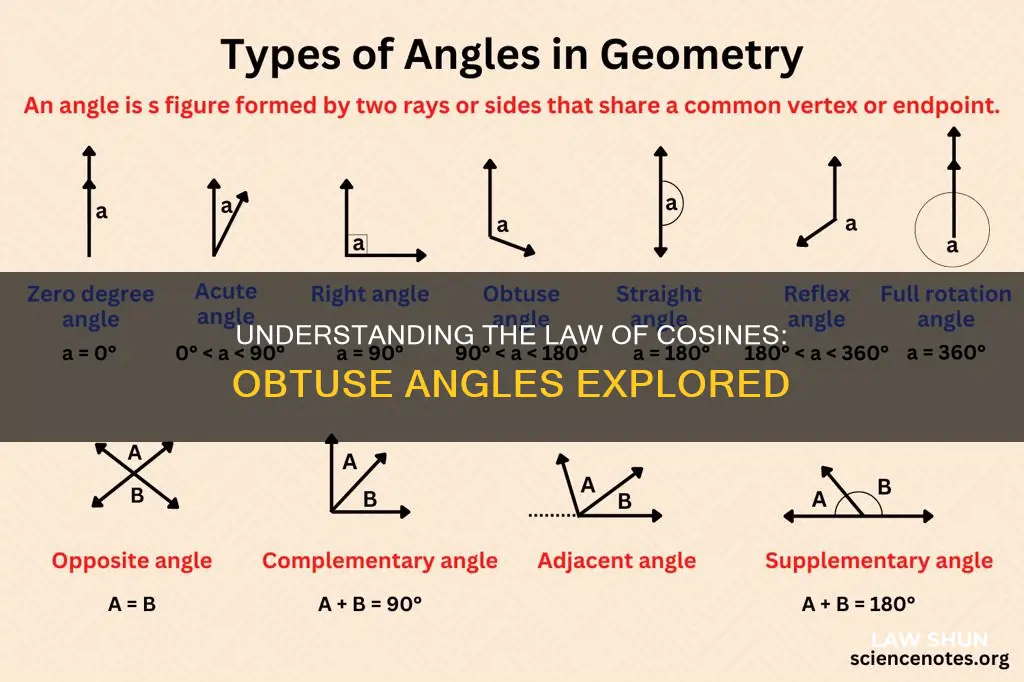
Where c, a, and b are sides, and C is the angle opposite side c. The law of cosines can be used for both acute and obtuse triangles. The cosine of an obtuse angle is always negative.
| Characteristics | Values |
|---|---|
| General formula | c2 = a2 + b^2 - 2ab cos(C) |
| Pythagorean Theorem | a2 + b2 = c^2 |
| Cosine of obtuse angle | -1 |
| Sine of obtuse angle | 0 |
What You'll Learn
- The law of cosines is a generalisation of the Pythagorean theorem
- The cosine rule can be used to find the third side of a triangle when two sides and the angle between them are known
- The cosine rule can be used to find the angles of a triangle when all three sides are known
- The cosine of an obtuse angle is always negative
- The cosine rule is also known as the cosine formula

The law of cosines is a generalisation of the Pythagorean theorem
The Pythagorean theorem states that for a right-angled triangle with sides a, b, and c, where c is the hypotenuse, a^2 + b^2 = c^2. The law of cosines takes this further by stating that a^2 = b^2 + c^2 - 2bc cos(A). Here, A is the angle opposite side a.
The law of cosines can be used to find the third side of a triangle when two sides and the angle between them are known, or to find the angles of a triangle when all three sides are known.
For example, let's say we have a triangle with sides a = 9, b = 5, and c unknown, and we want to find the value of c. Using the law of cosines, we can set up the equation:
C^2 = a^2 + b^2 - 2ab cos(C)
C^2 = 9^2 + 5^2 - 2(9)(5) cos(60)
C^2 = 81 + 25 - 90(0.5)
C^2 = 106
C = 10.3
So, the length of the unknown side c is approximately 10.3.
The law of cosines can also be used to find an angle in a triangle when all three sides are known. For example, let's consider a triangle with sides a = 8, b = 6, and c = 7, and we want to find the value of angle C. Using the law of cosines, we can set up the equation:
C^2 = a^2 + b^2 - 2ab cos(C)
7^2 = 8^2 + 6^2 - 2(8)(6) cos(C)
49 = 64 + 36 - 96 cos(C)
49 = 100 - 96 cos(C)
41 = -96 cos(C)
Cos(C) = 41/96
C = cos^-1(41/96)
C = 57.9 degrees
So, the measure of angle C is approximately 57.9 degrees.
The law of cosines is a versatile tool that can be used to solve triangles of any type, making it a valuable addition to the Pythagorean theorem, which is limited to right-angled triangles.
Kepler's Third Law: Moons Included?
You may want to see also

The cosine rule can be used to find the third side of a triangle when two sides and the angle between them are known
The law of cosines, or the cosine rule, is a formula in trigonometry that relates the lengths of the sides of a triangle to the cosine of one of its angles. The rule is:
C^2 = a^2 + b^2 - 2ab cos(C).
The rule can be used to find the third side of a triangle when two sides and the angle between them are known. For example, if we know that angle C = 37º, and sides a = 8 and b = 11, we can use the rule to find the length of side c:
C^2 = 8^2 + 11^2 - 2 x 8 x 11 x cos(37º)
C^2 = 64 + 121 - 176 x 0.798...
C^2 = 44.44...
C = √44.44 = 6.67 to 2 decimal places
The cosine rule is a generalisation of the Pythagorean theorem, which only applies to right triangles. The cosine rule can be used for all triangles, including obtuse triangles.
The cosine of an obtuse angle is always negative.
Sharia Law and Non-Muslims: Who Does It Affect?
You may want to see also

The cosine rule can be used to find the angles of a triangle when all three sides are known
The law of cosines, or the cosine rule, is a trigonometric rule that relates the lengths of the sides of a triangle to the cosine of one of its angles. The rule is:
For a triangle with sides a, b, and c, and angles α, β, and γ, the law of cosines states:
C^2 = a^2 + b^2 - 2abcosγ
A^2 = b^2 + c^2 - 2bccosα
B^2 = a^2 + c^2 - 2accosβ
The law of cosines can be used to find the angles of a triangle when all three sides are known. This is particularly useful when dealing with obtuse triangles, as the Pythagorean theorem only applies to right triangles.
To find the angle of an obtuse triangle when all three sides are known, the law of cosines can be used. The formula for the law of cosines is modified slightly to account for the obtuse angle. The cosine of an obtuse angle is always negative.
For example, let's say we have an obtuse triangle with sides a = 9, b = 6, and c = 8. We want to find the measure of angle C, which is opposite side c.
Using the law of cosines formula for finding an angle, we get:
Cos(C) = (a^2 + b^2 - c^2) / (2ab)
Plugging in our values, we get:
Cos(C) = (9^2 + 6^2 - 8^2) / (2*9*6) = 57.9°
So, the measure of angle C in this obtuse triangle is approximately 57.9 degrees.
The law of cosines is a versatile tool that can be used to solve triangles, whether they are right, acute, or obtuse. It is an extension of the Pythagorean theorem and can be derived using various methods, including the unit circle, Pythagorean theorem, and trigonometric identities.
HVAC and Lemon Law: What's the Connection?
You may want to see also

The cosine of an obtuse angle is always negative
The cosine rule can be used to find the third side of a triangle when we know two sides and the angle between them, or to find the angles of a triangle when we know all three sides. The formula for the law of cosines is:
C^2 = a^2 + b^2 - 2ab cos(C)
Where:
- C, a, and b are sides
- C is the angle opposite side c
The cosine rule can be derived from the Pythagorean theorem by applying it to each of the two right triangles formed by dropping a perpendicular from one vertex onto the side opposite the angle of interest. This proof handles cases of obtuse and acute angles in a unified fashion.
Antitrust Laws: Global Reach and Overseas Application
You may want to see also

The cosine rule is also known as the cosine formula
The law of cosines, also known as the cosine formula or cosine rule, is a fundamental concept in trigonometry that relates the lengths of the sides of a triangle to the cosine of one of its angles. This formula can be applied to any triangle, whether it has acute, obtuse, or right angles.
The cosine rule is particularly useful when solving triangles, and it can be used to find the length of the third side of a triangle when the lengths of the other two sides and the angle between them are known. It can also be used to determine the angles of a triangle when the lengths of all three sides are given.
The formula for the law of cosines is:
C^2 = a^2 + b^2 - 2ab * cos(C)
Where 'a', 'b', and 'c' represent the sides of the triangle, and 'C' is the angle opposite side 'c'.
When dealing with obtuse angles, it is important to remember that the cosine of an obtuse angle is always negative. This is because, in the context of a unit circle, the cosine value represents the x-component of the hypotenuse, which will be negative for angles in the second quadrant (obtuse angles).
The law of cosines can be derived using various methods, including algebraic manipulations, geometric proofs, and applications of other trigonometric identities such as the law of sines. It is a versatile tool in trigonometry and has analogues in spherical and hyperbolic geometry as well.
Understanding Commercial Property Rights: Tenant and Landlord Laws
You may want to see also
Frequently asked questions
Yes, the law of cosines can be used to find the cosine of an obtuse angle. The law of cosines is a more general formula that works for all types of triangles, not just right triangles.
To calculate the cosine of an obtuse angle, you can use the law of cosines formula:
c^2 = a^2 + b^2 - 2ab * cos(C)
Where:
- c is the side opposite the angle C
- a and b are the other two sides of the triangle
- C is the obtuse angle
Yes, the law of cosines can be used to find the angles of a triangle when the lengths of all three sides are known. Here is the formula:
cos(C) = (a^2 + b^2 - c^2) / (2*a*b)
Where:
- a, b, and c are the lengths of the sides of the triangle
- C is the angle opposite side c