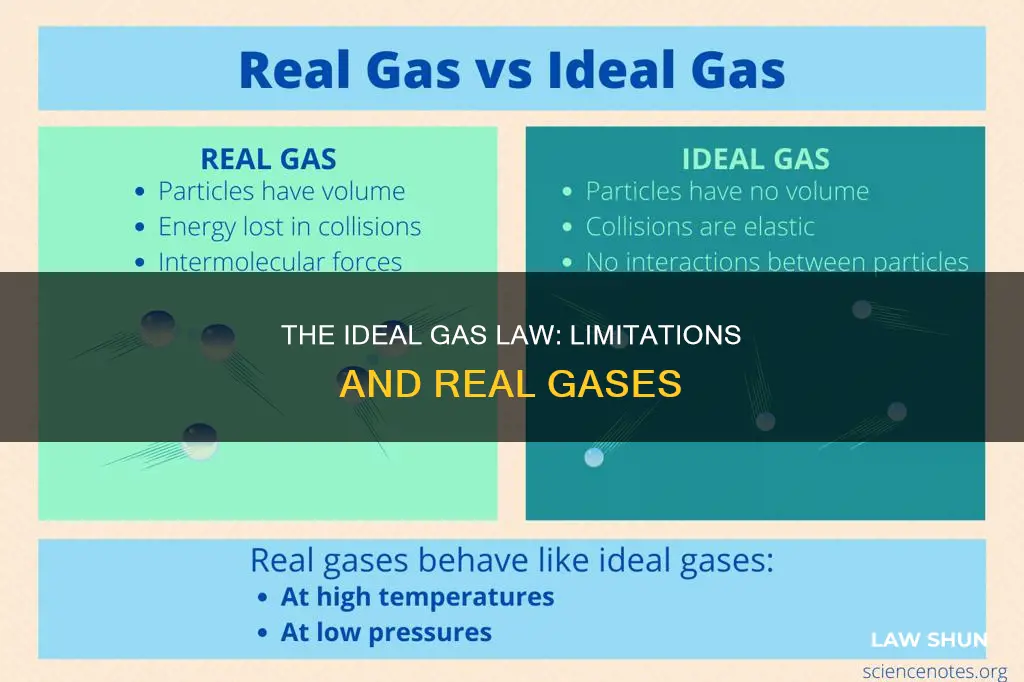
The ideal gas law is an equation that demonstrates the relationship between temperature, pressure, and volume for gases. However, it does not apply to real gases because it is based on certain assumptions that are not true in reality. These assumptions include the gas particles having negligible volume compared to the total volume of gas, the gas particles being equally sized without intermolecular forces, the gas particles moving randomly in agreement with Newton's laws of motion, and the gas particles having perfect elastic collisions with no energy loss or gain. In reality, all gases have nonzero molecular volumes, and the molecules of real gases interact with one another in ways that depend on their structure. Real gases deviate from ideal gas behaviour at high pressures and low temperatures, and they approach ideal behaviour at higher temperatures and lower pressures.
| Characteristics | Values |
|---|---|
| Gas particles have volume | In reality, gas particles have a volume within the system, violating the first assumption of ideal gas. |
| Gas particles are of different sizes | Gas particles vary in size; for example, hydrogen gas is significantly smaller than xenon gas. |
| Gas particles experience intermolecular forces | Gas particles exhibit intermolecular forces with adjacent gas particles, especially at low temperatures when they move slowly and interact with each other. |
| Gas particles do not have perfect elastic collisions | Gas particles move randomly but do not have perfect elastic collisions due to the conservation of energy and momentum within the system. |
| Ideal gas law does not account for chemical reactions | The ideal gas law does not consider chemical reactions in the gaseous phase, which can change the system's pressure, volume, or temperature. |
| Ideal gas law is based on certain assumptions | The ideal gas law assumes gas particles have negligible volume, are equally sized, experience no intermolecular forces, move randomly, and have perfect elastic collisions. |
| Real gases behave ideally under certain conditions | Real gases can behave ideally when subjected to very low pressures or high temperatures. |
What You'll Learn

Real gases have non-zero volume
At low pressures, the molecules of a real gas are relatively far apart, but as pressure increases, the distance between molecules decreases. This means that the volume occupied by the molecules becomes significant compared to the volume of the container. As a result, the total volume of a real gas is greater than the volume predicted by the ideal gas law.
At very high pressures, the experimentally measured value of PV/nRT is greater than the value predicted by the ideal gas law. This is because the ideal gas law does not account for the volume of gas particles, which means there is less space for them to move around in the container.
The Van der Waals equation of state is often used to model real gas behaviour, as it takes into account the volume of gas particles and the intermolecular interactions.
Sunlight and Earth: Inverse Square Law's Applicability
You may want to see also

Intermolecular forces are present
The ideal gas law assumes that gas particles do not interact with each other, and hence, there are no intermolecular forces. However, in reality, gas particles do interact with each other through intermolecular forces, which can be both attractive and repulsive. These forces become particularly prominent at low temperatures and high pressures, where the average distance between molecules is shorter.
At low temperatures, gas particles move slowly, and the effect of intermolecular forces becomes more pronounced. The attractive forces between the molecules reduce the number of collisions with the container wall, leading to a decrease in pressure exerted by the gas. This results in the observed pressure being lower than expected.
Additionally, at high pressures, the intermolecular distances become smaller, and the volume occupied by the molecules becomes significant compared to the volume of the container. Consequently, the total volume of the gas is greater than predicted by the ideal gas law.
The van der Waals equation modifies the ideal gas law to account for these intermolecular forces. It includes terms that correct for the volume occupied by the molecules and the reduction in pressure due to attractive forces. The equation introduces two empirical constants, 'a' and 'b', which are specific to each gas and reflect the strength of intermolecular forces.
The ideal gas law, therefore, does not account for the presence of intermolecular forces, which significantly influence the behaviour of real gases, particularly under conditions of high pressure and low temperature.
Applying to Law School: A Step-by-Step Guide
You may want to see also

Ideal gases are theoretical
Ideal gases are indeed theoretical constructs. In reality, no ideal gases exist.
For a gas to be ideal, four governing assumptions must be true. Firstly, the gas particles must have a negligible volume compared to the total volume of gas. Secondly, the gas particles must be of equal size and must not have intermolecular forces, such as attraction or repulsion, with other gas particles. Thirdly, the gas particles must move randomly in agreement with Newton's laws of motion that describe kinetic energy. And lastly, the gas particles must have perfect elastic collisions with no energy loss or gain.
However, in reality, all gases have a nonzero volume. For instance, the volume of hydrogen gas is significantly smaller than that of xenon gas. Furthermore, gas particles do experience intermolecular forces with adjacent gas particles, especially at low temperatures when their movement slows down. Additionally, gas particles do not have perfect elastic collisions due to the conservation of energy and momentum within the system.
Despite this, real gases can behave ideally under certain conditions. Real gases behave ideally when subjected to either very low pressures or high temperatures. Low-pressure systems allow gas particles to experience fewer intermolecular forces with other gas particles. Similarly, high-temperature systems enable gas particles to move faster and exhibit fewer intermolecular forces. Therefore, real gases can be treated as ideal for calculation purposes in either low-pressure or high-temperature systems.
HVAC and Lemon Law: What's the Connection?
You may want to see also

Real gases behave ideally under certain conditions
The ideal gas law is an equation that demonstrates the relationship between temperature, pressure, and volume for gases. It is based on four assumptions: the gas particles have negligible volume compared to the total volume of gas; the gas particles are equally sized and do not have intermolecular forces with other gas particles; the gas particles move randomly in agreement with Newton's laws of motion; and the gas particles have perfect elastic collisions with no energy loss or gain.
However, in reality, ideal gases do not exist. Any gas particle possesses a volume, no matter how minute, violating the first assumption. Gas particles also vary in size, and they do exhibit intermolecular forces with adjacent particles, especially at low temperatures. While gas particles do move randomly, they do not have perfect elastic collisions due to the conservation of energy and momentum within the system.
Despite this, real gases can behave ideally under certain conditions. This occurs when they are subjected to either very low pressures or high temperatures. Low-pressure systems allow gas particles to experience fewer intermolecular forces with other gas particles. Similarly, high-temperature systems enable gas particles to move quickly and exhibit fewer intermolecular forces. Thus, real gases can be treated as ideal for calculation purposes in either low-pressure or high-temperature systems.
The ideal gas law also holds for a system containing multiple ideal gases, known as an ideal gas mixture. In such a mixture, the total pressure of the system is the sum of the partial pressures of each gas particle.
Trampoline Product Safety: Business Law Essentials
You may want to see also

Ideal gas law has versatile applications
The ideal gas law, represented by the equation PV=nRT, where P is pressure, V is volume, n is the number of moles of gas, R is the universal gas constant, and T is absolute temperature, has versatile applications in various fields.
The ideal gas law can be used to determine the fourth property of a gas if the other three are known. For example, if the pressure, volume, and temperature of a gas are known, the ideal gas law can be used to calculate the number of moles of gas present. This law is particularly useful in stoichiometry problems, where the volume of gas produced or consumed in a chemical reaction needs to be determined.
Additionally, the ideal gas law can be used to calculate the molar volume of a gas at standard temperature and pressure (STP) conditions. STP is defined as a temperature of 273 K and a pressure of 100 kPa or 1 atm. At STP, any gas will have a molar volume of 22.4 L per mole, which is a useful approximation for stoichiometry calculations.
The ideal gas law also has applications in healthcare and medicine. For instance, it can be used to calibrate anesthetic mixtures in anesthesia machines, ensuring accurate and safe delivery of anesthetic gases to patients. Furthermore, it can be applied to respiratory physiology, helping clinicians understand and manage ventilation and gas exchange in the lungs.
Moreover, the ideal gas law can be used to determine thedensity of gases. By knowing the identity of the gas, its molar mass, and its volume and pressure conditions, the density can be calculated. This is particularly useful in industrial and laboratory settings where knowledge of gas density is essential for safety and handling.
While the ideal gas law is a useful approximation, it is important to recognize that real gases may deviate from ideal behavior under certain conditions, especially at high pressures and low temperatures. The van der Waals equation is often used to account for these deviations by considering the volume of gas molecules and intermolecular forces.
Lemon Law: Where You Buy or Register?
You may want to see also
Frequently asked questions
The ideal gas law assumes that gas particles have negligible volume, no intermolecular forces, move randomly, and have perfectly elastic collisions. However, real gas particles have volume and are affected by intermolecular forces, especially at low temperatures and high pressures.
The ideal gas law fails at low temperatures and high pressures due to the low volume occupied by the gas. Real gases behave ideally under very low pressures or high temperatures.
Real gases deviate from ideal behaviour at high pressures and low temperatures. At high pressures, the volume occupied by gas particles becomes significant, increasing the total volume. At low temperatures, intermolecular forces become more pronounced, reducing the pressure exerted by the gas.







