The inverse square law states that the intensity of a specified physical quantity is inversely proportional to the square of the distance from the source of that physical quantity. In other words, as the distance from the source increases, the intensity of the energy it emits decreases. This law applies to many forms of energy, including light, sound, and radiation. As such, it is relevant to understanding the sunlight that reaches Earth from the Sun. The inverse square law can be used to calculate how much sunlight reaches Earth compared to other planets in the solar system, and it is also important for designing solar-powered spacecraft.
| Characteristics | Values |
|---|---|
| Definition | Any scientific law stating that the observed "intensity" of a specified physical quantity is inversely proportional to the square of the distance from the source of that physical quantity |
| Formula | {displaystyle {\text}\ \propto \ {\frac {1}{{\text}^{2}}},} |
| Application | Used to measure astronomical distances |
| Other names | Lambert's first law |
What You'll Learn

Light intensity decreases with distance from the Sun
The inverse square law can be applied to understand the decrease in light intensity from the Sun as you move away from it. The law states that the intensity of light is inversely proportional to the square of the distance from the source. This means that if you double the distance from the source of light, the intensity of the light will decrease by four times (to one-quarter of its original intensity). Similarly, if you triple the distance, the intensity will decrease by nine times (to one-ninth of its original intensity), and so on.
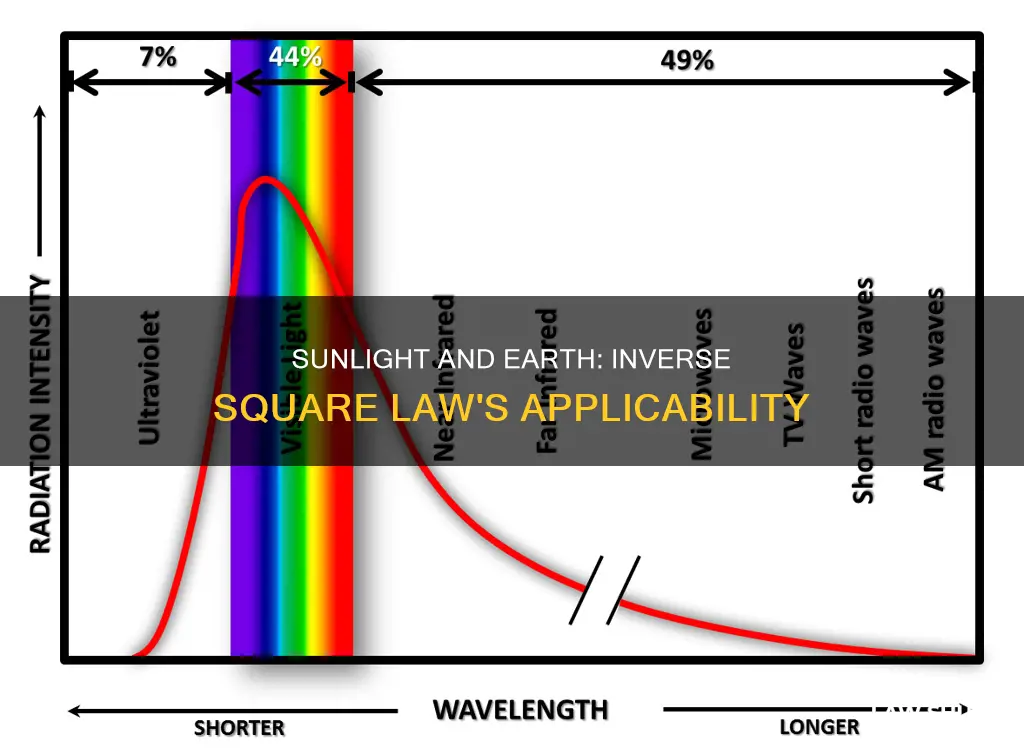
For example, let's consider the amount of sunlight received on different planets in our solar system. Earth is on average 149,597,870.66 kilometers (or 1 Astronomical Unit, or AU) away from the Sun, and it receives 1 solar constant of sunlight. Mars, which is 1.5 AUs from the Sun, receives only about 44% of the sunlight that Earth does. Jupiter, at 5.2 AUs, receives only about 3.7% of the sunlight that Earth does. As we move further out, to Neptune, which is 30 AUs from the Sun, the sunlight intensity decreases drastically to just 0.1% of what Earth receives!
The inverse square law can also be applied to other forms of energy, such as heat, ultraviolet rays, and X-rays, and even gravitational force. In the case of sunlight, the law helps us understand the variation in sunlight intensity across different planets, which has implications for the potential for life on those planets. Additionally, understanding this law is crucial for designing and operating spacecraft that rely on solar power, as the intensity of sunlight decreases significantly as the spacecraft travels further away from the Sun.
In summary, the inverse square law states that light intensity decreases with the square of the distance from the source. This law applies to sunlight, resulting in varying intensities of sunlight on different planets in our solar system. It also has practical applications in fields such as space exploration and photography, where understanding light intensity is essential for technological design and artistic endeavours.
Lemon Laws: Do They Apply to Campers?
You may want to see also

The inverse square law and solar power
The inverse square law states that the intensity of light or electromagnetic radiation from a point source is inversely proportional to the square of the distance from that source. In other words, as the distance from the source increases, the intensity of the radiation decreases, and this relationship can be expressed mathematically as I ∝ 1/d^2, where I is the intensity and d is the distance. This law is applicable in various fields, including optics, telecommunications, and solar energy.
In the context of solar power, the inverse square law helps explain the decrease in sunlight intensity as one moves away from the Sun. The law describes how the same amount of sunlight from the Sun is spread out over an increasingly larger spherical area as the distance increases. This results in a "dilution" of photon density, leading to a decrease in irradiance or illuminance on the expanding surface.
For example, let's consider the amount of sunlight reaching the Earth compared to other planets in our solar system. The average distance from the Sun to Earth is approximately 150 million km, or 1 Astronomical Unit (AU). At this distance, the Earth receives about 1367 watts per square meter (W/m^2) of solar radiation, which we can refer to as 1 solar constant.
Now, let's apply the inverse square law to calculate the amount of sunlight received by other planets. Mars, at a distance of 1.5 AUs from the Sun, receives only about 44% of the sunlight that Earth does. Jupiter, at 5.2 AUs, receives only 3.7% of Earth's sunlight, and on Neptune, which is 30 AUs from the Sun, the noon illumination is comparable to deep twilight on Earth, with only 0.1% of Earth's sunlight reaching its surface.
The inverse square law also works in the opposite direction, as we move closer to the Sun. Mercury, at a distance of 0.387 AUs, receives almost seven times more sunlight than Earth (about 666.67% more).
The implications of the inverse square law are significant for solar-powered spacecraft. As a spacecraft travels farther from the Sun, the amount of sunlight available for conversion into energy decreases significantly. To compensate for this, spacecraft travelling to distant planets require larger solar arrays or panels to collect enough solar energy to meet their power needs. For instance, NASA's Juno spacecraft, which orbited Jupiter, and the Europa Clipper mission, which will study Jupiter's moon Europa, have much larger solar arrays compared to spacecraft operating closer to the Sun.
In summary, the inverse square law is a fundamental principle that governs the behaviour of light and electromagnetic radiation, including sunlight. It has practical applications in various fields, including solar power, where it is essential for designing and operating spacecraft that rely on solar energy for distant missions.
Stark Law and Physical Therapists: Understanding the Legal Boundaries
You may want to see also

The inverse square law in photography
The inverse square law is a scary phrase for photographers, bringing to mind complex physics and equations. However, it is an essential concept for photographers to understand if they want to create well-lit images. In simple terms, the law states that as the distance from a light source increases, the intensity of light falls off very quickly and the light spreads out over a larger area. This means that light intensity or brightness drops much faster closer to the source than it does further away.
For photographers, this translates to harsher shadows and quicker light dissipation when the subject is closer to the light source. Moving the subject further away from the light source will result in dimmer light, softer shadows, and the light spreading over a larger area. This is important to consider when photographing groups of people to ensure even lighting across the group. It also impacts the tone and brightness of the background.
The inverse square law is particularly relevant when using studio lighting and off-camera flash, but it applies to all light sources, including natural light. For example, doubling the distance between a subject and a window will result in a 75% drop in light intensity.
Photographers can use the inverse square law to their advantage by manipulating the distance between the subject, light source, and background to achieve the desired lighting effects. A common mistake photographers make is placing the light source too close to the subject, resulting in uneven lighting. By understanding and applying the inverse square law, photographers can improve their lighting setups and create more consistent images with less trial and error.
Examples and Applications
- Lighting Setup: If your light meter measures F/11 when your studio flash is 5 feet from the subject, and you double the distance to 10 feet, the light intensity decreases by two full F-stops. To compensate and properly expose your image, you would need to adjust your lens aperture to F/5.6.
- Background Lighting: By placing your subject 10 feet from the background and the light source 5 feet from the subject, the inverse square law ensures that the light intensity on the background is at least a quarter of the light intensity on the subject, creating a darker background.
- High-Key Photography: In a high-key photo shoot, you can move the subject closer to the background than the light source to increase the brightness of the background.
- Low-Key Photography: To ensure a black background stays dark in a low-key scenario, the distance between the subject and the light source should be at least half or less than the distance between the subject and the background.
- Skin Tone Differences: When photographing two people with different skin tones, the inverse square law can be used to ensure even lighting. Place the darker-toned subject closer to the main light and the lighter-toned subject towards the fill light or backlight.
- Hair Color Differences: When photographing a subject with blonde or lighter hair than their face, the difference in F-stop between the hair and the face can be minimized by moving the light source further away.
- Group Photography: When photographing groups with rows of people, the inverse square law can be used to ensure even lighting across the rows. Place the light source at an appropriate distance to minimize the difference in light intensity between the rows.
Nevada Lemon Law: Does It Cover Boat Owners?
You may want to see also

The inverse square law and the brightness of the Sun from other planets
The inverse square law states that the intensity of light or energy from a point source is inversely proportional to the square of the distance from that source. In other words, as the distance from the source increases, the intensity of the light or energy decreases, and this relationship can be expressed mathematically as I ∝ 1/d^2, where I is the intensity and d is the distance. This law applies to various phenomena, including light, sound, and radiation, and is relevant in fields such as engineering, physics, and space exploration.
Now, let's apply this law to the brightness of the Sun as observed from different planets in our solar system. The Sun is a point source of light and energy, and the law dictates that as we move farther away from it, the brightness of the Sun will decrease. This is because, at a greater distance, the same amount of light and energy from the Sun is spread out over a larger area, resulting in a decrease in intensity.
Mercury, being the closest planet to the Sun at a distance of 0.387 astronomical units (AU), experiences a much brighter Sun than Earth. Using the inverse square law, we find that Mercury receives about 9126 watts per square meter of solar radiation, compared to Earth's 1367 watts per square meter at 1 AU. This is a significant difference and illustrates how the Sun's brightness decreases rapidly with distance.
For planets farther away from the Sun, the effect becomes even more pronounced. Mars, at 1.5 AUs, receives less than half the sunlight intensity compared to Earth. Jupiter, at 5.2 AUs, only receives about 3.7% of the sunlight intensity that Earth does. By the time we reach Neptune, at a distance of 30 AUs, the Sun's brightness has diminished to a mere 0.1% of what we experience on Earth. Noon on Neptune is akin to deep twilight on Earth!
The inverse square law, therefore, provides a clear understanding of the Sun's brightness from various planets in our solar system. It demonstrates that the Sun's energy and light intensity decrease rapidly with distance, resulting in significantly reduced brightness for planets farther away from the Sun. This law is crucial in astronomy and space exploration, helping us comprehend the varying illumination conditions on different planets and influencing the design of spacecraft and their power requirements for missions to distant celestial bodies.
Lead Paint Laws: Who Is Accountable?
You may want to see also

The inverse square law and other electromagnetic radiation
The inverse square law is a scientific law that states that the "intensity" of a physical quantity is inversely proportional to the square of the distance from the source of that physical quantity. In other words, as the distance from the source increases, the intensity of the quantity decreases, and this relationship is described by the inverse square law. This law generally applies to any force, energy, or conserved quantity that is evenly radiated outward from a point source in three-dimensional space.
Now, let's discuss the inverse square law in the context of electromagnetic radiation.
The Inverse Square Law and Electromagnetic Radiation
The inverse square law is applicable to various forms of electromagnetic radiation, including visible light and other frequencies of the electromagnetic spectrum. As light or electromagnetic waves travel away from their source, their intensity decreases following the inverse square law. This means that the intensity of the waves is inversely proportional to the square of the distance from the source. Mathematically, this can be expressed as I ∝ 1/d^2, where I is the intensity and d is the distance from the source.
The inverse square law for electromagnetic radiation has important implications and applications. For example, it is used in the design of solar panels for spacecraft travelling to distant planets. As the distance from the Sun increases, the amount of sunlight available decreases, and larger solar arrays are required to collect sufficient energy. This relationship is described by the inverse square law, which helps engineers determine the necessary size of solar panels for specific missions.
Additionally, the inverse square law can be applied to other forms of electromagnetic radiation, such as heat, ultraviolet rays, X-rays, and even gravity. By understanding this law, we can compare the intensity of these radiations at different distances from their sources. For instance, using the inverse square law, we can calculate that Jupiter, being five times farther from the Sun than Earth, receives only 1/25 the amount of sunlight as Earth.
In summary, the inverse square law is a fundamental principle that helps us understand the behaviour of electromagnetic radiation, including light and other frequencies. It describes how the intensity of radiation decreases as we move away from the source, and it has practical applications in fields such as astronomy, engineering, and physics.
Boyle's Law: Liquids and Gases Explored
You may want to see also
Frequently asked questions
The inverse square law states that the intensity of a specified physical quantity is inversely proportional to the square of the distance from the source of that physical quantity. In other words, as the distance from the source increases, the intensity of the energy it emits decreases.
The inverse square law applies to sunlight on Earth because the Sun is a point source of light/energy that radiates outward in three-dimensional space. As the distance from the Sun increases, the surface area of the sphere over which the same amount of light/energy is spread increases by the square of the distance. This means that the intensity of sunlight/energy on Earth is inversely proportional to the square of the distance from the Sun.
The inverse square law affects the amount of sunlight received on other planets in the solar system in a similar way to Earth. For example, Mars is 1.5 times further from the Sun than Earth, so it receives approximately 44% of the amount of sunlight that Earth receives. Jupiter, which is 5.2 times further from the Sun, receives only 3.7% of the amount of sunlight that Earth receives.