The Universal Gas Law: Why Does It Work?

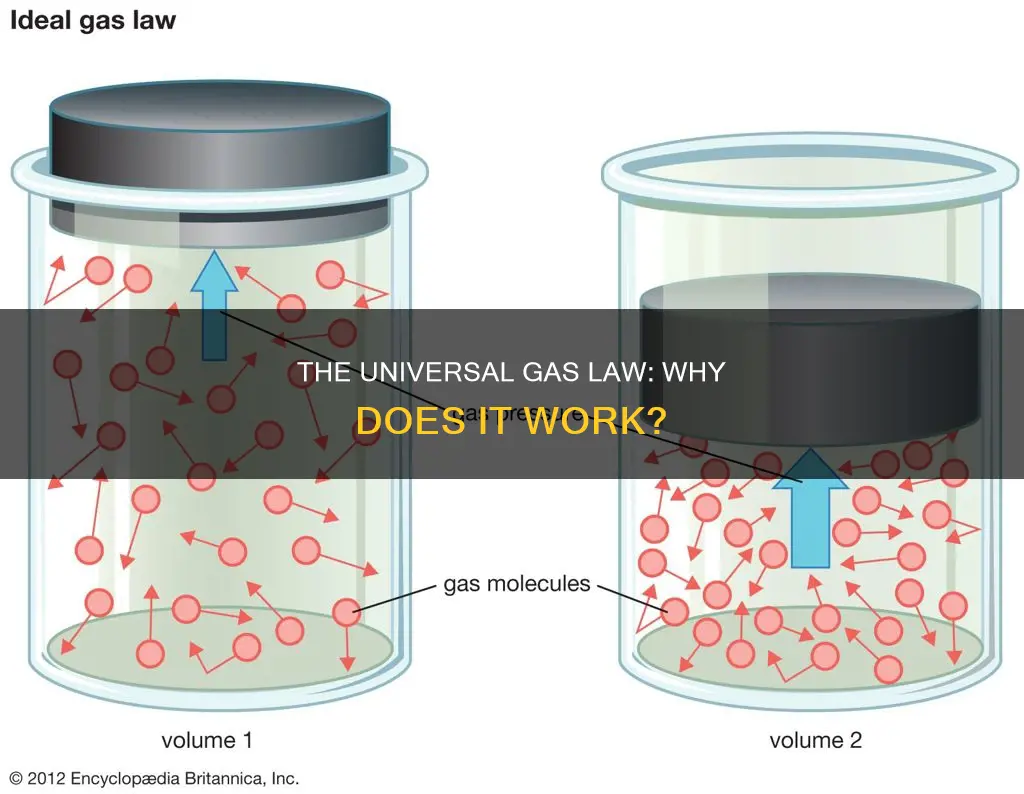
The ideal gas law, also known as the general gas equation, is an equation that describes the relationship between the pressure, volume, and temperature of a gas. It is a good approximation of the behaviour of many gases under various conditions, although it does have some limitations. The ideal gas law is PV = nRT, where P is the pressure, V is the volume, n is the number of moles of gas, R is the universal gas constant, and T is the absolute temperature. This law can be derived from the kinetic theory of gases, which assumes that gas molecules have negligible volume, do not interact, and move randomly with no loss of energy during collisions. While no real gas has these properties, the ideal gas law closely describes the behaviour of real gases under most conditions, particularly at low pressures and high temperatures.

The ideal gas law is a good approximation of the behaviour of many gases under many conditions

The ideal gas law is expressed as:

PV = nRT

Where P is the pressure, V is the volume, n is the number of moles of gas, R is the universal gas constant, and T is the absolute temperature. The ideal gas law is a good approximation of the behaviour of many gases because it assumes that gas particles have negligible volume compared to the total volume of a gas, and that gas particles are equally sized and do not have intermolecular forces, such as attraction or repulsion, with other gas particles. Additionally, it assumes that gas particles move randomly in agreement with Newton's laws of motion that describe kinetic energy, and that gas particles have perfect elastic collisions with no energy loss or gain.

While these assumptions do not perfectly describe real gases, they are a good approximation under certain conditions. Real gases behave ideally when subjected to either very low pressures or high temperatures. Low-pressure systems allow gas particles to experience fewer intermolecular forces with other gas particles, while high-temperature systems allow gas particles to move quickly and exhibit fewer intermolecular forces. Therefore, the ideal gas law is a good approximation for real gases under conditions of low pressure or high temperature.

The ideal gas law can also be applied to systems containing multiple ideal gases, known as an ideal gas mixture. In such cases, the ideal gas equation can be rewritten as:

PiV = niRT

Where Pi is the partial pressure of species i and ni are the moles of species i. Ideal gas mixtures are useful for easy calculations at low-pressure or high-temperature conditions.

In summary, the ideal gas law is a good approximation of the behaviour of many gases under many conditions because it makes simplifying assumptions about gas particles that hold true in certain situations, particularly low-pressure and high-temperature conditions.

The ideal gas law is a combination of Boyle's law, Charles's law, Avogadro's law, and Gay-Lussac's law

The ideal gas law is a combination of four empirical laws: Boyle's law, Charles's law, Avogadro's law, and Gay-Lussac's law. Each of these laws describes the behaviour of gases under certain conditions.

Boyle's law states that the volume of a given amount of gas held at a constant temperature varies inversely with the applied pressure when the temperature and mass are constant. In other words, decreasing the volume of a contained gas will increase its pressure, and vice versa.

Charles's law describes the relationship between the volume and temperature of a given amount of gas at constant pressure. It states that the volume of a given amount of gas is directly proportional to its temperature on the Kelvin scale when the pressure is held constant.

Avogadro's law gives the relationship between the volume and amount of gas in moles when pressure and temperature are held constant. It states that equal volumes of all gases, measured under the same conditions of temperature and pressure, contain the same number of molecules.

Gay-Lussac's law, also known as Amontons' law, describes the relationship between the pressure and temperature of a gas when the volume is held constant. It states that the pressure of a given amount of gas is directly proportional to its temperature on the Kelvin scale.

By combining these four laws, scientists established the ideal gas law, which relates the pressure, volume, temperature, and number of moles of a gas. The ideal gas law is expressed as:

PV = nRT

Where p is the absolute pressure of the gas, V is the volume, n is the amount of substance (or number of moles), and T is the absolute temperature. R is the ideal gas constant, which can be calculated as the product of the Boltzmann constant and the Avogadro constant.

The ideal gas law provides a good approximation of the behaviour of many gases under various conditions, although it has some limitations. It is most accurate for monatomic gases at high temperatures and low pressures.

The ideal gas law applies to a system containing multiple ideal gases, known as an ideal gas mixture

The ideal gas law can be applied to a mixture of ideal gases by treating the mixture as a single entity. The pressure, volume, and temperature of the mixture are the same as those of the individual gases within it. The amount of substance (or number of moles) of the mixture is the sum of the amounts of substance (or number of moles) of the individual gases. The ideal gas constant, R, is the same for all ideal gases. Therefore, the ideal gas law for a mixture of ideal gases can be written as:

PV = (n1 + n2 + ... + nx)RT

Where P, V, and T are the pressure, volume, and temperature of the mixture, n1, n2, ..., nx are the amounts of substance (or number of moles) of the individual gases in the mixture, and R is the ideal gas constant.

The ideal gas law can be derived from basic principles but was originally deduced from experimental measurements of Charles' law (which states that the volume occupied by a gas is proportional to its temperature at a fixed pressure) and Boyle's law (which states that, for a fixed temperature, the product of pressure and volume is constant). The ideal gas law can also be derived from the kinetic theory of gases, which assumes that gas molecules are in constant, random motion and that the volume of the molecules is negligible compared to the volume occupied by the gas.

While no gas has the properties of an ideal gas, the ideal gas law describes the behaviour of real gases quite closely. However, a gas will deviate from ideal behaviour when it is near its condensation point, the temperature at which it liquefies.

The ideal gas law can be used to model the behaviour of certain plasmas and gaseous mixtures

The ideal gas law applies to all gases because it is a good approximation of the behaviour of many gases under many conditions. The ideal gas law, also called the general gas equation, is the equation of state of a hypothetical ideal gas. It was first stated by Benoît Paul Émile Clapeyron in 1834 as a combination of Boyle's law, Charles's law, Avogadro's law, and Gay-Lussac's law.

The ideal gas law also applies to systems containing multiple ideal gases, known as an ideal gas mixture. In such a system, the total pressure is partitioned into the partial pressure contributions of each gas particle. The ideal gas equation can be rewritten as:

PiV=niRT

Where Pi is the partial pressure of species i and ni are the moles of species i.

The ideal gas law can be used to calculate the density and molar mass of an ideal gas. The ideal gas law relates the properties of pressure, volume, temperature, and the number of moles of a gas. By rearranging the ideal gas equation to isolate volume and substituting into the density equation, we can calculate the density of a gas.

The ideal gas law is a useful tool in various fields, including chemistry, physics, biotechnology, and clinical medicine.

The ideal gas law can be used to calibrate gas mixtures for use in anaesthetics

The ideal gas law applies to all gases because it is a good approximation of the behaviour of many gases under many conditions. It is an equation demonstrating the relationship between temperature, pressure, and volume for gases. The ideal gas law is a combination of Boyle's law, Charles's law, Avogadro's law, and Gay-Lussac's law.

The ideal gas law states that PV = nRT, where P is the pressure, V is the volume, n is the number of moles of gas, R is the universal gas constant, and T is the absolute temperature. The universal gas constant R is a number that satisfies the proportionalities of the pressure-volume-temperature relationship. The temperature value in the ideal gas law must be in absolute units, either Rankine (°R) or Kelvin (K), to prevent the right-hand side of the equation from being zero, which violates the pressure-volume-temperature relationship.

The ideal gas law can be used to calculate the volume of oxygen available from a cylinder. For example, an oxygen 'E' cylinder has a physical volume of 4.7 L, at a pressure of 137 bar (13700 kPa or 1987 PSI). Applying the ideal gas law at room temperature, we can calculate the volume of oxygen available from the cylinder, assuming a negligible reduction in temperature as gas is removed. With a basal oxygen consumption of 250 ml/min for the average-sized adult, we can calculate how long the oxygen will last.

The ideal gas law can also be used to calculate the number of molecules in a cubic meter of gas at standard temperature and pressure (STP). At STP, the pressure is 1.01 x 10^5 Pa, the volume is 1.00 m^3, and the temperature is 273 K. Using the ideal gas law, PV = NkT, we can calculate that there are 2.68 x 10^25 molecules in a cubic meter of gas at STP.

In summary, the ideal gas law is a useful tool for calibrating gas mixtures for use in anaesthetics, as it provides a reasonably accurate description of the volumetric behaviour of anesthetic gas mixtures at atmospheric conditions. It can also be applied to calculate the volume of oxygen available from a cylinder and the number of molecules in a cubic meter of gas at STP.

Frequently asked questions