The Combined Gas Law: Plasma's Exception Or Rule?

The combined gas law combines Boyle's Law, Charles' Law, and Gay-Lussac's Law. It states that the ratio of the product of pressure and volume to the absolute temperature of a gas is equal to a constant. This law applies to ideal gases, but does it apply to plasma? Plasma is a unique state of matter that resembles a gas but consists of ions and electrons coexisting. It is created by striking a gas under fixed volume with an electrical discharge, causing it to become ionized. The behaviour of plasma is influenced by the electromagnetic interactions between its particles, which can lead to effects significantly different from those observed in neutral gases.

Plasma's electromagnetic interactions

Plasma is a state of matter that is distinct from solids, liquids, and gases. It is characterised by the presence of a significant portion of charged particles, which can be a combination of ions and electrons. These charged particles make plasma electrically conductive, and its behaviour is dominated by long-range electric and magnetic fields.

The electromagnetic interactions of plasmas can occur on various scales, from local interactions to those between distant celestial objects such as galaxies, stars, and planets. One example of a local electromagnetic interaction is the coupling between Earth's magnetosphere and ionosphere, which includes plasma circulation, plasma escape along field lines, and field-aligned particle acceleration.

On a larger scale, plasmas interact with magnetic fields, electromagnetic radiation, and other plasma populations. For instance, magnetic field lines connecting different plasma populations facilitate the transfer of mass, momentum, and energy. This results in the electromagnetic coupling of the two plasmas.

The presence of charged particles in plasma also enables interactions with electric fields. Plasma waves, for instance, can be classified as electromagnetic or electrostatic depending on the presence of an oscillating magnetic field. Plasma waves can further be categorised by the species that are oscillating and the direction of propagation relative to the stationary magnetic field.

Additionally, the dynamics of individual particles and the motion of plasma as a whole are governed by collective electromagnetic fields. These fields are very sensitive to externally applied fields, and this responsiveness is leveraged in many modern devices and technologies, such as plasma televisions.

In summary, the electromagnetic interactions of plasmas encompass a wide range of phenomena, from local interactions within the Earth's atmosphere to large-scale interactions between celestial bodies. These interactions are facilitated by the presence of charged particles in plasma, which enable responses to electric and magnetic fields, leading to various wave phenomena and technological applications.

The applicability of the ideal gas law

The ideal gas law, also called the general gas equation, is an equation that demonstrates the relationship between temperature, pressure, and volume for gases. The ideal gas law is often written in an empirical form: PV=nRT, where P is the pressure, V is the volume, n is the amount of substance (or number of moles), R is the ideal gas constant, and T is the absolute temperature. The ideal gas law is a good approximation of the behavior of many gases under many conditions, although it has several limitations.

For a gas to be considered ideal, four governing assumptions must be true:

• The gas particles have negligible volume compared to the total volume of the gas.
• The gas particles are equally sized and do not have intermolecular forces, such as attraction or repulsion, with other gas particles.
• The gas particles move randomly in agreement with Newton's laws of motion that describe kinetic energy.
• The gas particles have perfect elastic collisions with no energy loss or gain.

In reality, ideal gases do not exist. Any gas particle possesses a volume within the system, violating the first assumption. Gas particles also vary in size and exhibit intermolecular forces, especially at low temperatures. While gas particles move randomly, they do not have perfect elastic collisions due to the conservation of energy and momentum within the system.

Although ideal gases are theoretical constructs, real gases can behave ideally under certain conditions. Real gases behave ideally when subjected to either very low pressures or high temperatures. The low pressure of a system allows gas particles to experience fewer intermolecular forces with other gas particles. Similarly, high-temperature systems allow gas particles to move quickly within the system and exhibit fewer intermolecular forces. Therefore, real gases can be considered ideal for calculation purposes in either low-pressure or high-temperature systems.

While the ideal gas law may not hold exactly for plasma, it can still be a useful approximation in certain parameter ranges. For example, the Saha equation, which relates temperature and particle density, is often used to describe certain plasma systems. Additionally, in some cases, Debye shielding can render net electromagnetic effects negligible, making the ideal gas law a more reasonable approximation.

The role of temperature, pressure and volume

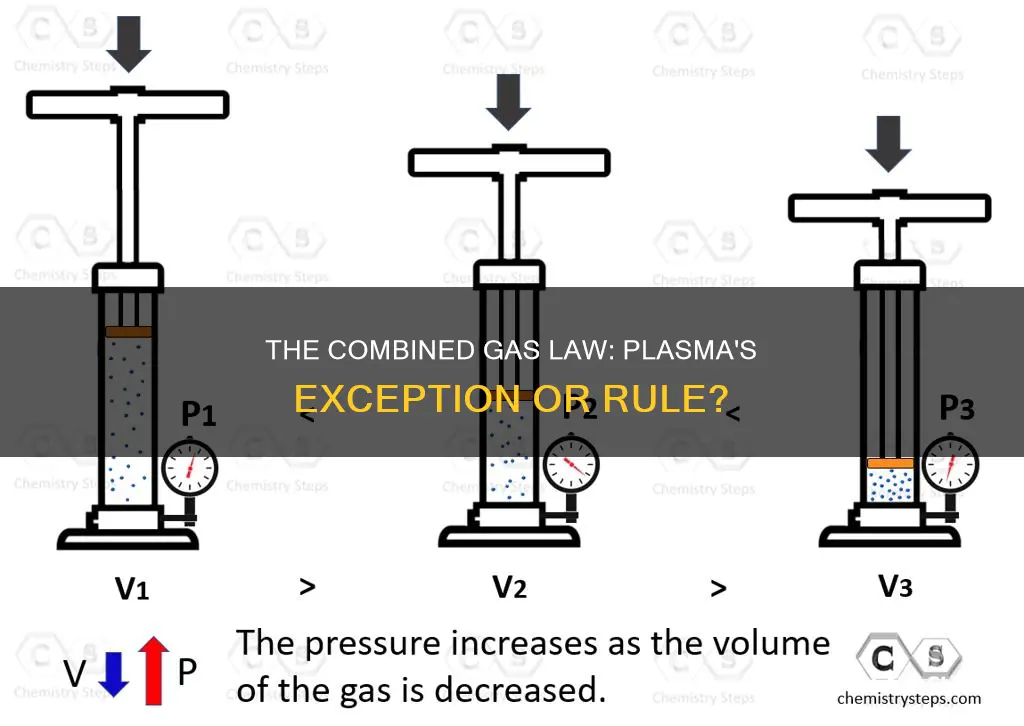
The combined gas law combines three gas laws: Boyle's Law, Charles' Law, and Gay-Lussac's Law. It states that the ratio of the product of pressure and volume to the absolute temperature of a gas is equal to a constant. The law gets its name from the fact that it combines these three laws and only applies when everything except temperature, pressure, and volume is held constant. The amount or number of moles of gas is kept constant.

The combined gas law plays a crucial role in understanding the behaviour of gases, particularly in relation to temperature, pressure, and volume. It allows us to predict how changes in one of these variables will affect the others. For example, if we know the initial conditions of a gas (pressure, volume, and temperature), we can use the combined gas law to calculate the final conditions after a change has been made to one of these variables.

Temperature plays a significant role in the combined gas law. As temperature increases, the kinetic energy of gas molecules also increases, leading to greater collisions and an increase in pressure. This relationship is described by the equation PV = nRT, where n is the number of moles and R is the gas constant. This equation demonstrates that pressure (P) and volume (V) are directly proportional to temperature (T) when the number of moles (n) is held constant.

Pressure and volume are also key factors in the combined gas law. According to Boyle's Law, pressure and volume are inversely proportional. This means that as the volume of a gas increases, the pressure decreases, and vice versa. This relationship can be observed when compressing a gas; as the volume decreases, the pressure increases.

The combined gas law also highlights the importance of understanding the absolute temperature of a gas. The law uses the Kelvin scale, which has a fixed starting point at absolute zero (-273.15°C). This fixed scale ensures consistency and accuracy when measuring temperature.

In summary, the combined gas law provides valuable insights into the behaviour of gases by examining the relationships between temperature, pressure, and volume. It allows us to make predictions and calculations about gas behaviour, particularly when dealing with gases at ordinary temperatures and pressures. By manipulating these variables, scientists and engineers can design and optimise systems involving gases, such as those used in thermodynamics and fluid mechanics.

The degree of ionization of the gas/plasma

The degree of ionization of a gas or plasma is a critical factor in determining whether the combined gas law applies to plasma. The degree of ionization refers to the proportion of neutral particles that are ionized, and it plays a significant role in understanding the behaviour of plasmas.

In plasma physics, the degree of ionization, denoted as alpha (α), is defined as the ratio of the number of ionized molecules (n_i) to the total number of molecules, which includes both ionized and neutral molecules (n_i + n_n). This value is usually expressed as a decimal number or a percentage. A low degree of ionization indicates a partially ionized plasma, while a high degree of ionization suggests a fully ionized state.

The degree of ionization is influenced by temperature and density. In the case of fully ionized matter, alpha (α) equals 1, indicating that all neutral particles have been ionized. This is often observed in very hot thermonuclear plasmas, such as those found in stars like our Sun.

Plasma, as a state of matter, is characterized by the presence of a significant portion of charged particles, which can be ions, electrons, or a combination of both. The transition to plasma from other states of matter is not well-defined and depends on interpretation and context. The degree of ionization becomes a crucial factor in determining whether a substance should be classified as plasma. While there is no precise threshold, a very low degree of ionization, even as little as 0.1%, can be sufficient for a gas to exhibit electromagnetic properties and behave as a plasma.

The distinction between fully ionized and partially ionized plasmas is important. In a fully ionized plasma, charged particle collisions dominate, whereas in a partially ionized plasma, collisions between charged particles and neutrals are more frequent. The transition between these two states can be abrupt, as described by Lehnert in 1970. As the input energy to the plasma gradually increases, the degree of ionization can suddenly jump from a fraction of 1% to full ionization.

In summary, the degree of ionization of the gas/plasma is a critical factor in understanding plasma behaviour and determining its classification. It refers to the proportion of neutral particles that have been ionized, and it influences the electromagnetic interactions within the plasma. The degree of ionization can vary significantly, and even a small fraction of ionized particles can lead to plasma-like behaviour. This makes the degree of ionization a key consideration when evaluating the applicability of the combined gas law to plasma.

The use of the Saha equation

The Saha equation, developed by physicist Meghnad Saha in 1920, is a crucial tool in physics that combines the principles of quantum mechanics and statistical mechanics. It relates the ionization state of a gas in thermal equilibrium to its temperature and pressure. This equation is particularly useful for gases at high temperatures or densities, where thermal collisions of atoms can lead to ionization and the formation of an ionized gas or plasma.

The Saha equation is expressed as:

> {\displaystyle {\frac {n_{i+1}n_{\text{e}}}{n_{i}}}={\frac {2}{\lambda _{\text{th}}^{3}}}{\frac {g_{i+1}}{g_{i}}}\exp \left [-{\frac {(\varepsilon _{i+1}-\varepsilon _{i})}{k_{\text{B}}T}}} ]}

Here, the variables represent the densities of atoms in different states of ionization, electron density, the Boltzmann constant, thermal de Broglie wavelength, and the energy required to remove electrons from a neutral atom.

The equation is applicable to weakly ionized plasmas with negligible Coulomb interactions between ions and electrons. It helps determine the ratio of particle densities at different ionization levels and has been instrumental in understanding stellar spectral sequences and the evolution of the early universe.

The Saha equation is an essential tool for understanding the behaviour of gases at high temperatures and densities, providing insights into the degree of ionization and the interactions between particles. It has been applied to explain various natural phenomena and has been a valuable contribution to the fields of physics and astrophysics.

Frequently asked questions