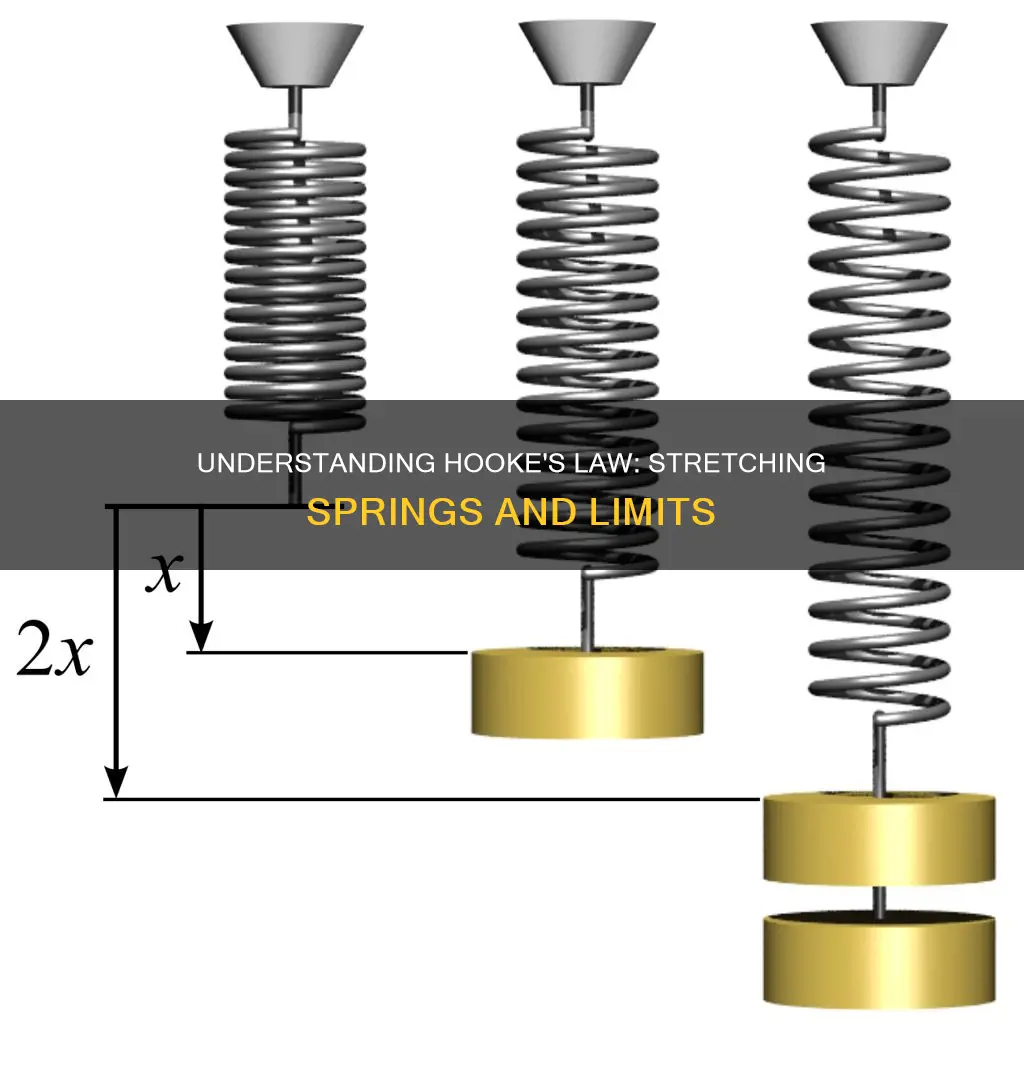
Hooke's Law is a fundamental principle of physics that explains the mechanics of springs. It states that the force required to extend or compress a spring is directly proportional to the distance of that extension or compression. In other words, the more you stretch or compress a spring, the greater the force it will exert in response. This law is named after 17th-century British physicist Robert Hooke, who first stated it in 1660 and later published the solution in Latin as ut tensio, sic vis, which translates to as the extension, so the force. Hooke's Law is not just limited to springs but also applies to many other situations involving elastic bodies, such as pulling a rubber band or inflating a balloon.
| Characteristics | Values |
|---|---|
| Named After | 17th-century British physicist Robert Hooke |
| Law States | The extension of a spring is proportional to the load that is applied to it |
| Equation | F = -kX, where F is the force applied to the spring, X is the displacement of the spring, and k is the spring constant |
| Law Type | Principle of physics |
| Application | Applicable to a wide range of springs, including compression, extension, torsion, and coil springs |
| Limitations | Only applies when the load does not exceed the material's elastic limit; many materials will deviate from the law before reaching this limit |
What You'll Learn

Hooke's Law and the extension of a spring
Springs are a marvel of human engineering and come in many varieties, including compression, extension, torsion, and coil springs. They are used in a wide range of applications, from automotive suspension systems to clocks, and even children's toys.
Hooke's Law is a fundamental principle of physics that explains the behaviour of springs and other elastic objects. Named after 17th-century British physicist Robert Hooke, it states that the force required to extend or compress a spring is directly proportional to the distance of that extension or compression. In other words, the extension of a spring is proportional to the load applied to it. This can be expressed mathematically as F= -kX, where F is the force, X is the displacement, and k is the spring constant, or a measure of the spring's stiffness.
Hooke's Law is considered the earliest explanation of the concept of elasticity, which is the property of an object that causes it to return to its original shape after being manipulated. This ability of an object to return to its original shape is known as the restoring force, and in the context of Hooke's Law, this force is generally proportional to the amount of stretch experienced.
While Hooke's Law is a useful approximation, it does have its limitations. It only applies when the forces and deformations involved are small. Beyond a certain point, materials will deviate from Hooke's Law before their elastic limit is reached, and permanent deformation or a change of state will occur.
In its general form, Hooke's Law is compatible with Newton's laws of static equilibrium, and it has applications in various scientific and engineering disciplines, including seismology, molecular mechanics, and acoustics. It is also the basis for many everyday inventions, such as the spring scale, the manometer, and the mechanical clock.
Employment Discrimination Law: Resident Aliens' Rights Explored
You may want to see also

The force needed to extend or compress a spring
Hooke's law is a fundamental principle of physics that explains the mechanics of springs. The law is named after 17th-century British physicist Robert Hooke, who sought to elucidate the relationship between the forces exerted on a spring and its resulting elasticity.
Hooke's law states that the force required to extend or compress a spring is directly proportional to the distance by which the spring is stretched or compressed. This relationship can be expressed mathematically as F = -kX, where F represents the force applied to the spring, X denotes the displacement of the spring from its equilibrium position, and k is the spring constant, indicating the stiffness of the spring.
The spring constant, k, is a critical factor in determining the behaviour of a spring under varying loads. It is a property of the spring that characterises its stiffness or resistance to deformation. The value of k depends on the physical characteristics of the spring, such as the material used, its length, and its cross-sectional area.
By using Hooke's law, we can calculate the force needed to extend or compress a spring by a certain distance. For example, if a spring has a spring constant of 8 lbf/in and we want to compress it by 0.25 inches, we can calculate the required force as F = kx = 8 lbf/in x 0.25 inches = 2 lbf.
Additionally, Hooke's law has broader applications beyond just springs. It can be applied to any elastic body or material that undergoes deformation, such as wind blowing on a tall building or a musician plucking a guitar string. This versatility has made Hooke's law a foundational principle in various scientific and engineering disciplines, including seismology, molecular mechanics, and acoustics.
Leash Laws in Alabama: Do Cats Need Them?
You may want to see also

The spring constant and stiffness
Hooke's Law, a principle of physics, states that the force required to extend or compress a spring is proportional to the distance it is extended or compressed. The law is named after 17th-century British physicist Robert Hooke, who sought to demonstrate the relationship between the forces applied to a spring and its elasticity.
The spring constant, also known as "k", is a measure of a spring's stiffness. It is a constant indicating how stiff a spring is and is represented in Newtons per meter (N/m). The higher the spring constant, the stiffer the spring, and the more force required to stretch it.
The spring constant is calculated using the formula F = -kx, where F is the force applied to the spring, and x is the displacement of the spring from its equilibrium position. The negative sign indicates that the force and displacement are in opposite directions.
For example, if a spring with an unknown spring constant supports a weight of 0.1 N, and adding another 0.1 N weight stretches the spring by 3.5 cm, we can calculate the spring constant as k = 2.85 N/m.
The spring constant is a crucial factor in understanding the behaviour of springs and designing them for specific applications. It helps determine the amount of force a spring can exert and how much it will stretch under a given load.
Laws and Fake Bald Eagles: Who's Protected?
You may want to see also

The restoring force
Hooke's Law, named after 17th-century British physicist Robert Hooke, states that the extension or compression of a spring is proportional to the force applied to it. Mathematically, this can be expressed as F = -kx, where F is the force, x is the displacement, and k is the spring constant, indicating the stiffness of the spring.
Shipping Laws: Home Brew and Wine, What's the Difference?
You may want to see also

The limits of Hooke's Law
Hooke's Law is a principle of physics that states that the force required to extend or compress a spring is directly proportional to the distance it is extended or compressed. However, this law has its limitations.
Firstly, it is important to note that Hooke's Law only applies to springs and other elastic bodies within a limited frame of reference. The law assumes that the spring will always return to its original shape after being manipulated, but this is not always the case. If a spring is compressed beyond a certain minimum size or stretched beyond a maximum size, it will undergo permanent deformation or a change of state. This means that Hooke's Law only holds true as long as the amount of force or deformation involved is relatively small. Many materials will noticeably deviate from Hooke's Law well before their elastic limits are reached.
In addition, Hooke's Law is a first-order linear approximation of the real response of springs and other elastic bodies to applied forces. It is based on the assumption that the relationship between the force applied to a spring and its elasticity is linear. However, in reality, this relationship may be nonlinear, especially when the spring is subjected to large deformations. Therefore, Hooke's Law is most accurate for small deformations and may not hold true for larger distortions.
Furthermore, Hooke's Law is based on the concept of elasticity, which is the ability of an object to return to its original shape after being manipulated. However, not all materials exhibit elastic behaviour. Some materials, such as rubber, are considered "non-Hookean" because their elasticity is stress-dependent and sensitive to factors like temperature and loading rate. In such cases, Hooke's Law may not accurately describe the behaviour of these materials.
Moreover, Hooke's Law assumes that the force required to extend or compress a spring is directly proportional to the distance it is extended or compressed, with the proportionality constant being the spring constant. However, this assumption may not hold true for all materials. Some materials may exhibit a non-linear relationship between force and distance, especially beyond the proportionality limit. The proportionality limit refers to the maximum stress or strain that an object can undergo before the relationship between stress and strain becomes non-linear.
Lastly, Hooke's Law is based on the assumption that the spring will always return to its equilibrium position after being displaced. However, in reality, various factors can affect the spring's ability to return to its original position, such as friction or the presence of a non-conservative force. These factors can lead to energy loss in the system, causing the spring's behaviour to deviate from the predictions of Hooke's Law.
Lemon Law: Beyond Cars?
You may want to see also
Frequently asked questions
Hooke's Law is a principle of physics that states that the force needed to extend or compress a spring is proportional to the distance it is extended or compressed.
The mathematical representation of Hooke's Law is F = -kX, where F is the force applied to the spring, X is the displacement of the spring, and k is the spring constant.
The spring constant, k, is a measure of the spring's stiffness.
No, Hooke's Law applies in many other situations where an elastic body is deformed, such as a musician plucking a guitar string or wind blowing on a tall building.
Hooke's Law applies to a variety of materials as long as the load does not exceed the material's elastic limit. However, many materials will noticeably deviate from Hooke's Law before the elastic limit is reached.







