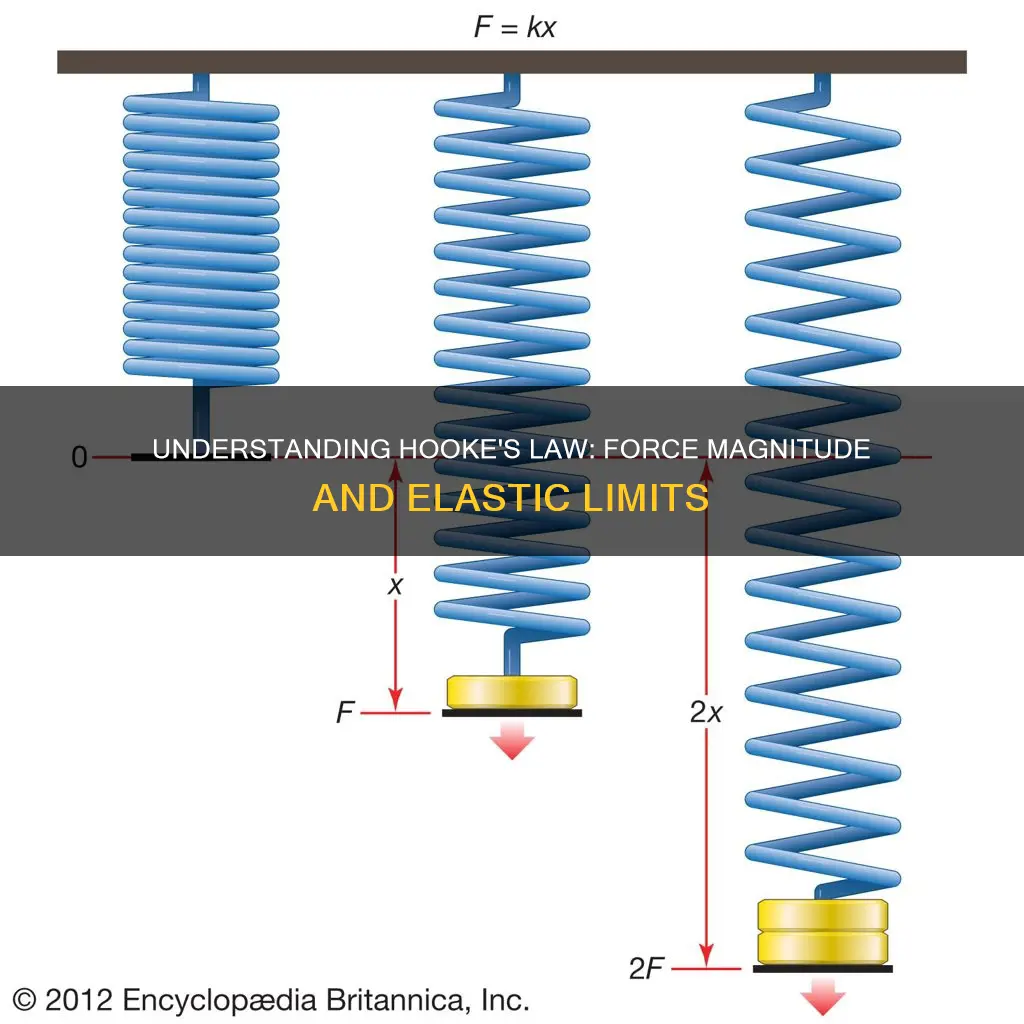
Hooke's law, F = kx, is a law of physics that states that the force (F) required to extend or compress a spring by some distance (x) is directly proportional to that distance. The law was discovered by British physicist Robert Hooke in the 17th century and states that for small deformations of an object, the displacement or size of the deformation is directly proportional to the deforming force or load. However, Hooke's law only holds true for limited amounts of force or deformation as materials can only be compressed or stretched to a certain extent without some permanent deformation.
| Characteristics | Values |
|---|---|
| Named After | 17th-century British physicist Robert Hooke |
| Equation | F = kx |
| Law | The force needed to extend or compress a spring by some distance is proportional to that distance |
| Spring Constant | k is a constant factor characteristic of the spring (i.e., its stiffness) |
| Stress | Force on unit areas within a material that develops as a result of the externally applied force |
| Strain | Relative deformation produced by stress |
| Stress-Strain Relationship | For small deformations, the stress and strain are proportional to each other |
| Elasticity | The property of an object or material which causes it to be restored to its original shape after distortion |
| Restoring Force | The ability of an elastic object to exert a force proportional to the displacement of the object and in the opposite direction |
| First Law of Thermodynamics | Any spring when compressed or extended almost perfectly conserves the energy applied to it |
What You'll Learn

Hooke's Law and the First Law of Thermodynamics
Hooke's Law is a fundamental principle of physics that states that the force required to extend or compress a spring by some distance is proportional to that distance. The law is named after 17th-century British physicist Robert Hooke, who formulated it in 1660 and published it in 1678.
Hooke's Law can be expressed mathematically as F = -kX, where F is the force applied to the spring, X is the displacement of the spring, and k is the spring constant. This law is a classical example of the explanation of elasticity, which is the property of an object or material that allows it to return to its original shape after experiencing distortion.
The First Law of Thermodynamics, also known as the Law of Conservation of Energy, states that energy cannot be created or destroyed but can only change from one form to another. This principle is closely related to Hooke's Law, as the energy stored in a spring due to its displacement is a form of potential energy, which is a fundamental concept in thermodynamics.
Hooke's Law demonstrates the conservation of energy by showing that a spring, when compressed or extended, almost perfectly conserves the energy applied to it. The only energy lost is due to natural friction. Additionally, Hooke's Law contains a wave-like periodic function, where a spring released from a deformed position will return to its original position with a proportional force in a periodic manner.
In summary, Hooke's Law and the First Law of Thermodynamics are connected through the concept of energy conservation. Hooke's Law illustrates the First Law of Thermodynamics by demonstrating that the energy applied to a spring is conserved as potential energy, apart from minor losses due to friction. This connection highlights the fundamental principles governing the behaviour of elastic objects and the conservation of energy in various physical systems.
Labor Laws: Contractors and California's Unique Rules Explained
You may want to see also

Hooke's Law and the conservation of energy
Hooke's Law, discovered by English scientist Robert Hooke in 1660, states that for small deformations of an object, the displacement or size of the deformation is directly proportional to the deforming force or load. This law is expressed mathematically as F = kx, where F is the applied force and x is the displacement or change in length. The value of k depends on the type of elastic material, as well as its dimensions and shape.
Hooke's Law is a fundamental principle in physics that describes the behaviour of elastic objects when subjected to forces. It is an empirical law, meaning it is based on observations and experiments rather than theoretical derivations. The law holds true for various elastic objects, including springs, rubber bands, and even tall buildings swaying in the wind.
The conservation of energy is a fundamental principle in physics that states that energy cannot be created or destroyed, only transformed from one form to another. In the context of Hooke's Law, the mechanical energy applied to a spring is conserved as it is compressed or extended. The potential energy stored in the spring is given by the equation U_el(x) = 1/2 kx^2, where x is the displacement and k is the spring constant. This equation demonstrates that the potential energy increases as the square of the displacement, meaning that the energy applied to the spring is conserved and transformed into potential energy within the spring.
Hooke's Law also plays a crucial role in understanding the behaviour of harmonic oscillators, such as a mass attached to a spring. When the mass is pulled and released, it exhibits oscillatory motion about the equilibrium position. The frequency of this motion is independent of its amplitude and is determined by the mass and stiffness of the spring, as given by the equation f = 1/2π * sqrt(k/m). This demonstrates that the conservation of energy is at play, as the energy applied to the system is transformed into kinetic and potential energy, with no loss of energy over time.
In summary, Hooke's Law provides a mathematical description of the relationship between force and displacement in elastic objects, while the conservation of energy ensures that the energy applied to these objects is neither created nor destroyed but merely transformed between different forms. Together, these principles form the foundation for understanding the behaviour of elastic objects and have numerous practical applications in fields such as engineering, seismology, and acoustics.
Sunshine Laws: Do They Shine on Property Owners Associations?
You may want to see also

Hooke's Law and the behaviour of springs
Hooke's law, discovered by English scientist Robert Hooke in 1660, is a fundamental principle of physics that describes the behaviour of springs and other elastic objects. It states that the force (F) required to extend or compress a spring is directly proportional to the displacement (x) of the spring from its equilibrium position. This relationship can be expressed mathematically as F = kx, where k is the spring constant, a measure of the spring's stiffness.
The law holds for relatively small deformations of a spring or other elastic object, where the object returns to its original shape and size after the load is removed. In this regime, the force exerted by the spring is known as a "restoring force" and acts to oppose the displacement, with the force and displacement having equal magnitudes but opposite directions. This means that the spring pushes or pulls with a force proportional to the displacement from its equilibrium position.
The spring constant, k, depends on the material and shape of the spring, as well as its dimensions. For a simple helical spring, the spring constant is directly proportional to its cross-sectional area and inversely proportional to its length.
While Hooke's law is a good approximation for most solid bodies, it has limitations and does not hold for all magnitudes of applied force. As the force or deformation increases beyond a certain point, the spring will deviate from Hooke's law and exhibit non-linear behaviour. This is because no material can be compressed beyond a certain minimum size or stretched beyond a maximum size without undergoing permanent deformation or a change of state. Therefore, Hooke's law only applies within the elastic limit of the material, where the relationship between force and displacement remains linear.
In summary, Hooke's law provides a useful framework for understanding the behaviour of springs and other elastic objects under relatively small deformations. However, it is essential to recognise its limitations and apply it within the context of its elastic limit to ensure accurate predictions of spring behaviour.
US Copyright Laws: Do They Apply in Russia?
You may want to see also

Hooke's Law and the behaviour of elastic materials
Hooke's Law is a fundamental principle of physics that explains the behaviour of elastic materials. It was discovered by the English scientist Robert Hooke in 1660 and states that, for relatively small deformations of an object, the displacement or size of the deformation is directly proportional to the deforming force or load.
Mathematically, Hooke's Law can be expressed as:
> F = kx
Where:
- F is the applied force
- K is a constant, known as the spring constant, which depends on the type of elastic material, its dimensions, and shape
- X is the displacement or change in length
Hooke's Law holds that the applied force is equal to the spring constant multiplied by the displacement. This means that if you double the force on an elastic object, its length will also double.
The law applies to a wide range of situations where an elastic body is deformed, such as a guitar string being plucked, a rubber band being stretched, or a tall building swaying in the wind. It also forms the basis for various inventions, including the manometer, spring scale, and the balance wheel of the mechanical clock.
However, Hooke's Law has limitations. It only holds true for relatively small deformations and within the elastic limit of the material. If the forces or deformations become too large, many materials will deviate from Hooke's Law, and permanent deformation or a change of state may occur.
In summary, Hooke's Law is a valuable tool for understanding the behaviour of elastic materials under specific conditions. It provides a linear approximation of how these materials respond to applied forces, as long as those forces do not exceed certain limits.
Hunting Season Laws: Your Yard, Their Rules?
You may want to see also

Hooke's Law and the behaviour of solid bodies
Hooke's Law is a fundamental principle of physics that explains the behaviour of solid bodies when subjected to external forces. The law was formulated by 17th-century British physicist Robert Hooke, who first stated it in 1660 as a Latin anagram and published the solution in 1678: "ut tensio, sic vis" ("as the extension, so the force" or "the extension is proportional to the force").
Hooke's Law states that the force (F) required to extend or compress a spring by some distance (x) is directly proportional to that distance. This relationship can be expressed mathematically as F = kx, where k is a constant factor known as the spring constant, which characterises the stiffness of the spring.
The law holds for relatively small deformations of an object, where the displacement or size of the deformation is directly proportional to the deforming force or load. In this regime, when the force is removed, the object returns to its original shape and size. This behaviour can be explained by the fact that small displacements of the object's constituent molecules, atoms, or ions from their normal positions are also proportional to the force causing the displacement.
The deforming force may be applied to a solid in various ways, including stretching, compressing, squeezing, bending, or twisting. For example, a metal wire exhibits elastic behaviour according to Hooke's Law because a small increase in its length when stretched by an applied force doubles each time the force is doubled.
While Hooke's Law provides a good approximation for most solid bodies, it has limitations and does not hold for all magnitudes of applied force. As the applied force increases, the deformation of the elastic material may become larger than expected based on Hooke's Law, even though the material remains elastic and returns to its original shape after the force is removed. This deviation from Hooke's Law occurs because it only describes the elastic properties of materials in the range where the force and displacement are proportional.
Beyond a certain point, known as the elastic limit, Hooke's Law ceases to be valid as materials can only be compressed or stretched to a certain extent without undergoing permanent deformation or a change of state. Many materials will deviate noticeably from Hooke's Law well before these elastic limits are reached.
In summary, Hooke's Law provides valuable insights into the behaviour of solid bodies under relatively small deformations, helping us understand how objects respond to external forces and return to their original shape. However, it is essential to recognise its limitations and consider more advanced theories, such as the modern theory of elasticity, when dealing with larger deformations or forces approaching the elastic limit of materials.
Disabled Texans and Minimum Wage Laws: Who's Exempt?
You may want to see also
Frequently asked questions
Hooke's Law is a principle of physics that states that the force needed to extend or compress a spring by some distance is proportional to that distance. It is named after 17th-century British physicist Robert Hooke, who first stated the law in 1660 as a Latin anagram.
Hooke's Law can be expressed mathematically as F = kx, where F is the applied force, x is the displacement or change in length, and k is a constant factor or "spring constant" that depends on the kind of elastic material under consideration.
Hooke's Law is important as it provides a basic understanding of the mechanics of springs, which have extensive applications in automotive suspension systems, clocks, hand shears, toys, and more. It also has applications beyond springs, as it describes the elastic behaviour of solids and is the foundation of disciplines such as seismology, molecular mechanics, and acoustics.
Hooke's Law only holds true for relatively small deformations of an object. Beyond a certain point, materials will deviate from Hooke's Law and may exhibit permanent deformation or change of state. It also does not apply to all materials, for example, rubber is considered a "non-Hookean" material.
Hooke's Law is compatible with Newton's laws of static equilibrium. Together, they allow us to deduce the relationship between strain and stress for complex objects in terms of the intrinsic properties of the materials they are made of.