Blaise Pascal, a French mathematician, physicist, and philosopher, formulated Pascal's Law in 1653, publishing it in 1663. Pascal's Law states that when there is an increase in pressure at any point in a confined fluid, there is an equal increase in pressure at every other point in the container. This principle is the foundation of hydraulics, which use incompressible fluids like oil or water to transmit forces from one location to another within the fluid. Hydraulic systems are used in a variety of applications, from car brakes to heavy-duty machinery, and understanding Pascal's Law is key to understanding how these systems function.
| Characteristics | Values |
|---|---|
| Pressure in an enclosed fluid | Uniform throughout a practical system |
| Equality of pressure | Pascal's law |
| Pressure | Force per unit area |
| Pressure change in a fluid | Transmitted undiminished to all portions of the fluid and to the walls of its container |
| Pressure at a point in a fluid | The same in all directions |
| Hydraulic systems | Used to operate automotive brakes, hydraulic jacks, and other mechanical systems |
What You'll Learn

Pressure changes in a confined fluid
Pascal's law, also known as Pascal's principle, states that when there is a change in pressure at any point in a confined fluid, there is an equal change throughout the fluid. This means that if pressure is increased at one point, it increases by the same amount everywhere in the fluid.
For example, consider a cylinder of fluid with a piston on top. If a weight is added to the piston, the pressure at the top of the fluid increases. According to Pascal's law, this pressure increase is transmitted undiminished to all parts of the fluid. So, the pressure at the bottom of the cylinder also increases by the same amount.
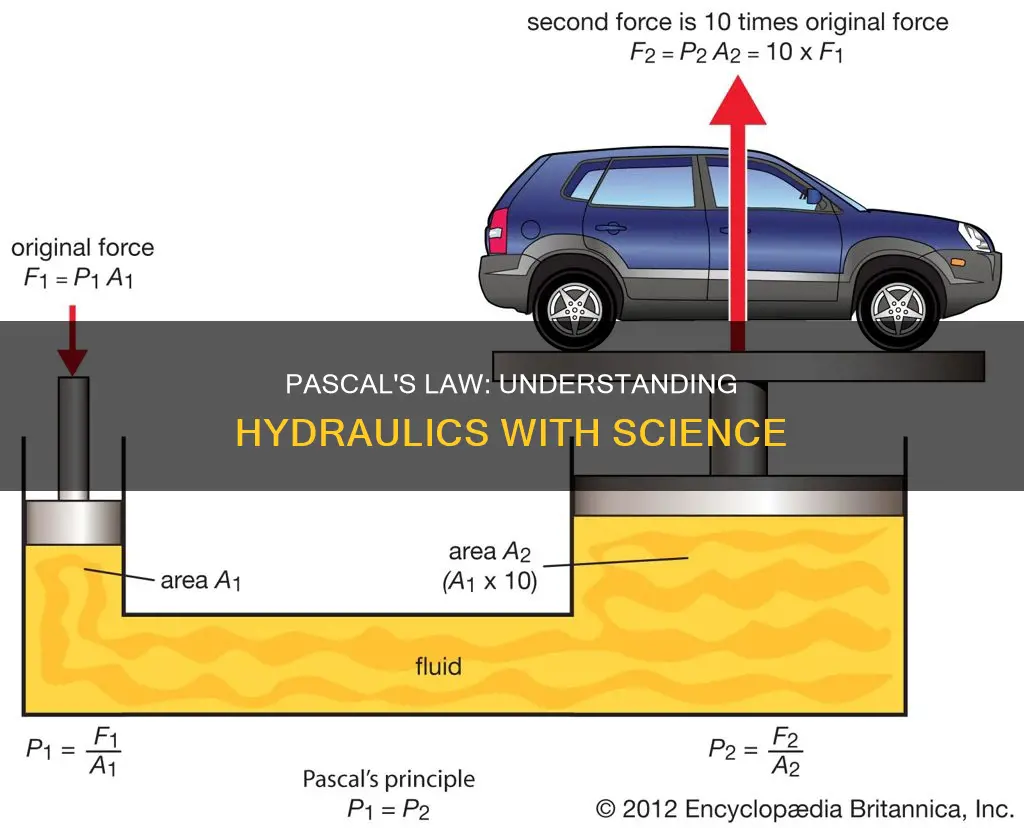
This principle can be applied to understand the functioning of hydraulic systems, which use an incompressible fluid such as oil or water to transmit forces. In a hydraulic system, a change in pressure applied to the fluid is transmitted equally in all directions. This allows for the multiplication of forces. For instance, in a hydraulic car lift, a small force acting on a small piston can generate a much larger force on a larger piston, enabling the lifting of heavy loads.
The formula for pressure change in a fluid column due to gravity is:
Δp = ρg x Δh
Where:
- Δp is the hydrostatic pressure or the difference in pressure at two points within the fluid column
- Ρ is the fluid density
- G is the acceleration due to gravity
- Δh is the height of the fluid above the point of measurement or the difference in elevation between two points
Pascal's law assumes that the fluid is incompressible, which means its density remains constant. This is important because the change in pressure between two elevations is directly related to the weight of the fluid between those elevations.
It is important to note that Pascal's law applies to confined fluids. This confinement ensures that the fluid cannot flow out and that the pressure changes are transmitted throughout the fluid. However, the specific shape of the container does not affect the application of the law.
Understanding Blue Laws: Who Does It Affect?
You may want to see also

Pressure distribution in a liquid
Pascal's Law states that any change in pressure at any point in a confined incompressible fluid is transmitted equally and undiminished in all directions throughout the fluid. In other words, if there is an increase in pressure at one point, there will be an equal increase at every other point in the container. This principle was established by French mathematician Blaise Pascal in 1653 and published in 1663.
The law can be understood through the following formula:
> {\displaystyle \Delta p=\rho g\cdot \Delta h\,} where:
- {\displaystyle \Delta p} is the hydrostatic pressure or the difference in pressure at two points within a fluid column due to the weight of the fluid.
- Ρ is the fluid density.
- G is the acceleration due to gravity.
- {\displaystyle \Delta h} is the height of the fluid above the point of measurement or the difference in elevation between two points.
This formula shows that the change in pressure between two elevations is due to the weight of the fluid between those elevations.
Pascal's Law has important implications for understanding pressure distribution in liquids. It demonstrates that pressure changes are transmitted uniformly throughout the fluid, regardless of the shape of the container. This means that if a force is applied to a confined fluid, the pressure created will act equally at right angles to the surfaces of the container.
For example, consider a U-tube filled with water and pistons at each end. If pressure is exerted on the left piston, it will be transmitted through the water and against the bottom of the right piston. The pressure exerted by the left piston will be equal to the pressure exerted by the water against the right piston.
By changing the piston's area, the force can be multiplied. If the tube on the right is made wider and a piston with a larger area is used, the pressure exerted will be the same, but the force will be greater due to the increased area. This principle allows for the multiplication of forces and is the basis for many mechanical applications, including hydraulic car lifts and jacks.
In summary, Pascal's Law describes the uniform distribution of pressure in liquids, where any change in pressure is transmitted equally throughout the fluid. This law has significant applications in hydraulics and helps explain the behaviour of liquids under pressure.
Applying Early to Penn Law: A Smart Decision?
You may want to see also

Hydraulic systems and force multiplication
Hydraulic systems use incompressible fluids, such as oil or water, to transmit forces from one location to another within the fluid. Pascal's law states that when there is an increase or decrease in pressure at any point in a confined fluid, there is an equal increase or decrease at every other point in the container. This means that any change in pressure applied to an enclosed fluid is transmitted undiminished throughout the fluid and to the walls of its container.
Pascal's law can be interpreted as saying that any change in pressure applied at any given point of the fluid is transmitted undiminished throughout the fluid. This principle is the basis of hydraulic systems, which can increase or decrease the force applied to them. For example, if a 100-N force is applied to a cylinder with a certain area and the connected cylinder has five times the area, then the output force is 500 N.
The formula for this relationship is:
> F2 = F1 * (A2 / A1)
Where:
- F1 = Force applied
- A1 = Cross-sectional area of the first piston
- A2 = Cross-sectional area of the second piston
- F2 = Resulting force
This principle is used in hydraulic car lifts, where the cylinder on the left has a smaller cross-sectional area than the cylinder on the right. A small force acting on the smaller piston can lift a much larger weight on the larger piston. The mechanical advantage of such a system can be calculated as follows:
> Mechanical Advantage (MA) = D1 / D2 = A2 / A1
Where:
- D1 = Distance moved by the smaller piston
- D2 = Distance moved by the larger piston
The larger the cross-sectional area of the second piston, the larger the mechanical advantage, and the more weight it can lift.
Hydraulic systems are used in a wide range of applications, including automotive brakes, hydraulic jacks, and numerous other mechanical systems. They are analogous to simple levers but have the advantage that pressure can be transmitted through curved lines to multiple locations simultaneously.
Florida Fertilizer Laws: Homeowner Compliance Requirements
You may want to see also

Pascal's law and mechanical advantage
Pascal's law, also known as Pascal's principle, states that any increase in pressure at a point in a confined incompressible fluid is transmitted undiminished throughout the fluid. In other words, pressure applied at any point in a contained incompressible fluid is transmitted equally in all directions throughout the entire enclosed fluid. This is true regardless of the shape of the container.
Pascal's law can be applied to understand the functioning of hydraulic systems, which use an incompressible fluid (e.g. oil or water) to transmit forces from one location to another within the fluid. For example, in a hydraulic car lift, an increase in pressure on a small piston can cause a much larger increase in pressure on a larger piston, resulting in a multiplied force that can lift a heavy load. This is known as mechanical advantage.
The mechanical advantage of a hydraulic system can be calculated using the formula:
> Mechanical Advantage (IMA) = D1/D2 = A2/A1
Where D1 and D2 are the distances moved by the smaller and larger pistons, respectively, and A1 and A2 are the cross-sectional areas of the smaller and larger pistons, respectively.
The larger the cross-sectional area of the second piston (A2) relative to the first piston (A1), the larger the mechanical advantage, and the more weight can be lifted. This is because the pressure increase is distributed equally across the larger piston's greater area, resulting in a larger force.
Pascal's law and the concept of mechanical advantage are thus fundamental to understanding the operation of hydraulic systems, allowing for the multiplication of forces and the lifting of heavy loads with relatively small input forces.
International Law: Domestic Legal Systems and Their Applications
You may want to see also

Hydraulic power transmission
There are two main types of hydraulic power transmission systems: hydrokinetic and hydrostatic. Hydrokinetic systems, such as hydraulic couplings and torque converters, utilise the kinetic energy of the fluid. A hydraulic coupling links two rotatable shafts and consists of a vaned impeller on the drive shaft and a similar vaned runner on the driven shaft, both enclosed in a casing containing a fluid, usually oil. If there is no resistance to the turning of the driven shaft, it will rotate at the same speed as the drive shaft. However, when a load is applied to the driven shaft, it slows down, and a torque is developed. A hydraulic torque converter is similar but includes a stationary vaned member between the runner and the impeller, which results in a greater torque on the driven shaft compared to the drive shaft.
On the other hand, hydrostatic systems use the pressure energy of the fluid and are commonly used in machine tools, farm machinery, coal mining machinery, and printing presses. This type of system combines hydraulic pumps and motors, which can be separated and connected by piping. An example of a hydrostatic system is one using pressurised water, built in London in 1882, which is still used to drive machinery for lifting bridges and operating hoists.
Hydraulic power systems offer greater flexibility than mechanical and electrical systems and can produce more power compared to systems of equal size. They are widely used in modern aircraft, automobiles, and heavy industrial machinery due to their ability to provide rapid and accurate responses to controls. Motors in hydraulic power systems can be classified as linear motors or rotational motors. Linear motors, or hydraulic cylinders, consist of a piston and a cylindrical outer casing, and they are useful for applications requiring high-force, straight-line motion, such as brake cylinders in automobiles. Rotational motors, or rotary hydraulic motors, produce rotary motion by using pressurised fluid to act on the surfaces of the motor's gear teeth, vanes, or pistons, creating torque on the output shaft. These motors are commonly used in digging equipment, printing presses, and spindle drives on machine tools.
Lemon Law Limitations: Florida's Focus Beyond Faulty Cars
You may want to see also
Frequently asked questions
Pascal's Law, also known as Pascal's Principle, states that any increase in pressure at a point in a confined incompressible fluid is transmitted equally throughout the fluid, resulting in an equal increase in pressure at every other point.
Hydraulic systems use incompressible fluids like oil or water. When force is applied to one piston, the fluid transmits this force uniformly and undiminished in all directions, including to the other piston, regardless of the shape of the container or connecting tubes.
A hydraulic car lift or jack is a great example. A small force applied to a small piston can lift a much heavier load on a larger piston. The force is transmitted through the fluid, and the larger piston area results in a larger force output.
Pascal's Law is used in automotive brakes, syringes, and clamps, as well as in scuba diving equipment and artesian wells.
Blaise Pascal, a French mathematician and physicist, observed that pressure in a fluid is independent of the container's shape and that pressure changes are transmitted undiminished throughout an enclosed fluid. These insights form the basis of Pascal's Law and have wide-ranging applications in hydraulics.







