Ampere's Law is a fundamental principle in electromagnetism, named after Andre-Marie Ampere. It states that the line integral of the magnetic field around a closed loop is proportional to the net electric current enclosed by that loop. In simpler terms, Ampere's Law helps us understand the relationship between magnetic fields and the electric currents that create them. This law is particularly useful for calculating magnetic fields generated by electric currents, which has practical applications in electromagnets, motors, generators, and transformers. By using Ampere's Law, we can simplify complex calculations involving symmetric systems of current elements. This law is an integral part of Maxwell's equations, which provide a comprehensive framework for understanding all electromagnetic phenomena.
| Characteristics | Values |
|---|---|
| Definition | The line integral of the magnetic field around an arbitrarily chosen path is proportional to the net electric current enclosed by the path |
| Formal Statement | For any closed loop path, the sum of the length elements times the magnetic field in the direction of the length element is equal to the permeability times the electric current enclosed in the loop |
| Integral Form | Integral(Bdl) = 0 |
| Extended Version | Contains the concept of displacement current |
| Main Usage | Calculating the magnetic field generated by an electric current |
| Other Usages | Electromagnets, motors, generators, transformers |
| Relation to Other Laws | Biot-Savart law, Gauss's law, Coulomb's law, Maxwell's equations |
What You'll Learn

Ampere's Law and its relation to Gauss's Law
Ampere's Law and Gauss's Law are both fundamental principles in electromagnetism, and they are interconnected in understanding the behaviour of electric and magnetic fields.
Ampere's Law states that the line integral of the magnetic field around an arbitrarily chosen path is proportional to the net electric current enclosed by the path. In simpler terms, it relates the magnetic field in space to the electric current that is its source, just as Gauss's Law relates the electric field in space to the charge that is its source.
Gauss's Law for electricity states that the electric flux out of any closed surface is proportional to the total charge enclosed within that surface. This law is a powerful tool for calculating electric fields, especially in cases with a lot of symmetry.
Ampere's Law is often used in conjunction with Gauss's Law for magnetism, which states that the net magnetic flux out of any closed surface is zero. This is because there is no such thing as a "magnetic monopole" or "magnetic charge". By combining these laws, one can calculate the magnetic field in cases with a high degree of symmetry.
The integral form of Ampere's Law states that the sum of the length elements along a closed loop path, multiplied by the magnetic field in the direction of that length element, is equal to the permeability times the electric current enclosed within the loop. This can be expressed mathematically as:
\[\co: 1>\oint \vec{B}\cdot \vec{d\ell}=\mu_o I_{\small THROUGH} \nonumber\]
Where:
- \(\co: 1>\oint\) indicates the closed loop integral
- \(\co: 1>\vec{B}\) is the magnetic field
- \(\co: 1>\vec{d\ell}\) is an infinitesimal length element of the closed loop
- \(\co: 1>\mu_o\) is the magnetic permeability of free space
- \(\co: 1>I_{\small THROUGH}\) is the electric current passing through the region enclosed by the loop
Ampere's Law can be applied to calculate the magnetic field generated by electric currents in various configurations, such as long straight conductors, solenoids, and toroids. By choosing an appropriate closed loop path, known as an Amperian Loop, one can use this law to determine the magnetic field at specific points or regions in space.
In summary, Ampere's Law and Gauss's Law are fundamental tools in electromagnetism that relate the electric or magnetic field to their respective sources (current and charge). Ampere's Law is particularly useful for calculating magnetic fields in symmetric systems, often in conjunction with Gauss's Law for magnetism, which accounts for the absence of magnetic monopoles.
Health and Safety Law: Charities' Legal Responsibilities
You may want to see also

The integral form of Ampere's Law
Ampere's circuital law relates the circulation of a magnetic field around a closed loop to the electric current passing through the loop. The law was discovered by André-Marie Ampère, who investigated the magnetic force between two current-carrying wires.
The direction of positive \(I_{encl}\) is the direction in which the fingers of the right hand intersect any surface \({\mathcal S}\) bordered by \({\mathcal C}\) when the thumb of the right hand points in the direction of integration.
The line integral of the magnetic field around an arbitrarily chosen path is proportional to the net electric current enclosed by the path. Ampere's Law can be used to calculate the magnetic field generated by an electric current, which has many practical applications in electromagnets, motors, generators, and transformers.
Lemon Law and Furniture: What's the Verdict?
You may want to see also

The differential form of Ampere's Law
Ampere's Law states that for any closed loop path, the sum of the length elements times the magnetic field in the direction of the length element is equal to the permeability times the net electric current enclosed in the loop.
Ampere's Law can be expressed as:
\[\oint\limits_{\textrm{loop}} \BB \cdot d\rr = \mu_0 \, I_{\textrm{enclosed}}\]
Where \(\oint\limits_{\textrm{loop}} \BB \cdot d\rr\) is the circulation of the magnetic field around any imaginary closed loop, and \(I_{\textrm{enclosed}}\) is the enclosed current.
The enclosed current is the flux integral of the current density through any surface bounded by the loop:
\[I_{\textrm{enclosed}} = \Int_{\textrm{surface}} \JJ\cdot d\AA\]
Stokes' Theorem tells us that the circulation integral can be replaced with the integral of the curl of the vector field over any surface bounded by the loop. Choosing the surface to be the same as the surface used to calculate the flux of the current:
\[\Int_{\textrm{surface}} \!\! (\grad\times\BB)\cdot d\AA = \mu_0 \Int_{\textrm{surface}} \!\! \JJ\cdot d\AA\]
Because this last relationship is true for any closed loop, we can conclude that the integrands themselves must be equal:
\[\grad\times\BB = \mu_0 \,\JJ\]
This is the differential form of Ampère's Law, and is one of Maxwell's Equations. It states that the curl of the magnetic field at any point is the same as the current density there. Another way of stating this law is that the current density is a source for the curl of the magnetic field.
Usury Laws and Overdraft Credit: What's the Verdict?
You may want to see also

Applying Ampere's Law to determine the magnetic field
Ampere's Law is a powerful tool for determining the magnetic field generated by electric currents. It states that for any closed loop path, the sum of the length elements multiplied by the magnetic field in the direction of the length element is equal to the permeability times the electric current enclosed in the loop. In simpler terms, it tells us that the line integral of the magnetic field around a closed path is proportional to the net electric current enclosed by that path.
To apply Ampere's Law, we choose an "Amperian loop", which is an imaginary loop that encloses the area where we want to calculate the magnetic field. This loop can be oriented in any direction, but it must be a closed path. The choice of the Amperian loop is crucial, just like the choice of Gaussian surfaces is important in Gauss's Law.
Once we have defined our Amperian loop, we can use the integral form of Ampere's Law:
$$\oint \vec{B}.d\vec{l} = \mu_{0} I _{encl}$$
Where:
- $\co: 3>\oint \vec{B}.d\vec{l}$ represents the line integral of the magnetic field $\co: 3>\vec{B}$ around the Amperian loop, with $\co: 3>d\vec{l}$ being an infinitesimal length element along the loop.
- $\co: 3>\mu_{0}$ is the permeability of free space, a fundamental constant in nature.
- $\co: 3>I _{encl}$ is the net electric current enclosed by the Amperian loop.
By using this equation, we can calculate the magnetic field at any point along the closed path. The direction of the magnetic field can be determined using the right-hand rule, also known as the "right-hand grip rule" or "RHR-2". Point your right thumb in the direction of the current, and your fingers will curl in the direction of the magnetic field loops created by it.
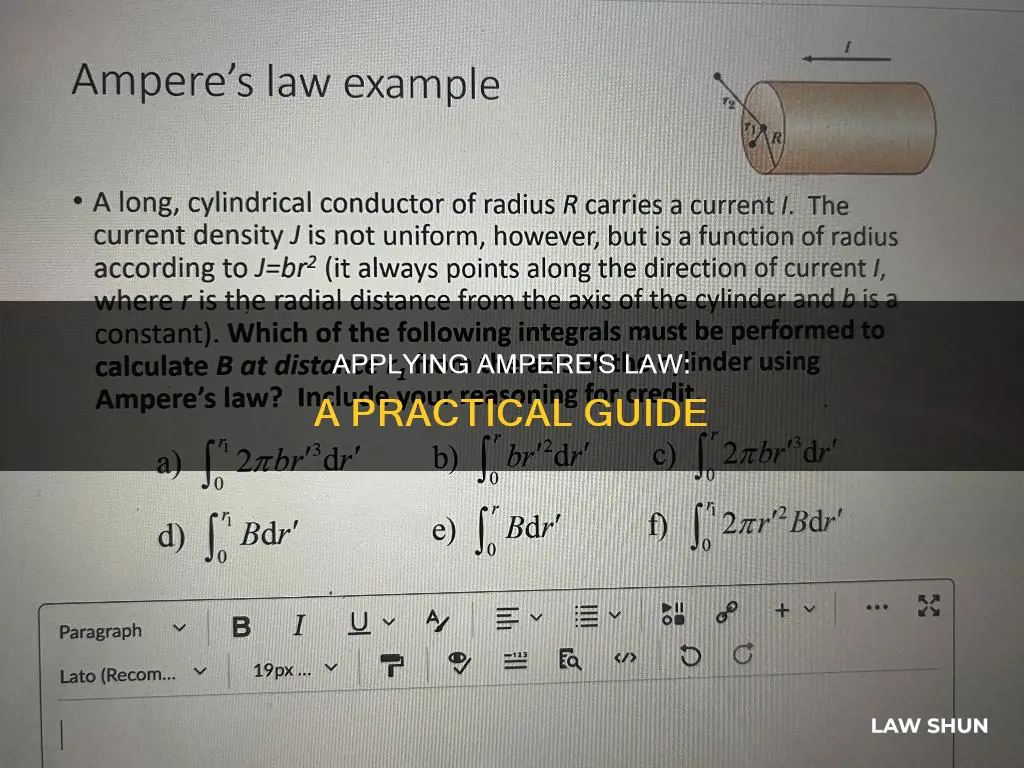
Ampere's Law is particularly useful for calculating the magnetic field generated by symmetric systems, such as long straight conductors, solenoids, and toroids. For example, consider a long straight conductor carrying a current $I$. By choosing an Amperian loop with radius $r$ centred at the wire, we can calculate the magnetic field $B$ as follows:
$$B = \frac{\mu_{0}I}{2 \pi} \frac{r}{R^{2}}$$
Where $R$ is the radius of the conductor. This calculation assumes that the current is uniformly distributed across the cross-sectional area of the conductor.
Ampere's Law also has applications beyond simple current-carrying wires. For instance, it can be used to determine the magnetic field inside a solenoid, which is a helical winding of wire on a cylinder. If the solenoid is long compared to its diameter and the coils are tightly wound, the internal magnetic field near the centre is uniform and parallel to the axis, while the external field is negligible. By applying Ampere's Law, we can show that the magnetic field inside such a solenoid is given by:
$$B = \mu_{0}nI$$
Where $n$ is the number of turns of wire per unit length, and $I$ is the current.
Generators and Idling: NYS Law Explained
You may want to see also

The limitations of Ampere's Law
Ampere's Law is a fundamental principle of electromagnetism that characterises the relationship between electric currents and the resulting magnetic fields. It is named after André-Marie Ampère, a scientist who, in the late 1820s, performed experiments with forces acting on current-carrying wires. Ampere's Law can be applied to determine the magnetic field surrounding a wire, inside a conductor, or created by a long current-carrying conducting cylinder. It can also be used to calculate the magnetic induction due to a long, straight conductor, a solenoid, or a toroid.
Despite its wide range of applications, Ampere's Law has several limitations. Firstly, it is only valid for steady, constant currents. It does not account for the effects of changing electric fields or the presence of a changing magnetic field. Ampere's Law is based on the assumption of an infinitely long, straight current-carrying wire, which may not always be the case in practical scenarios. Therefore, it cannot be used to calculate the magnetic field inside a material, as the field inside is influenced by the properties of the material.
To address these limitations, modifications have been made to Ampere's Law, such as the Ampere-Maxwell law, which includes the effects of changing electric fields, and the Biot-Savart law, which can determine the magnetic field at any point in space for a given current distribution. These modifications provide a more comprehensive understanding of the relationship between electric currents and magnetic fields, allowing for more accurate calculations and predictions.
Whistleblower Law: Can the President Be Held Accountable?
You may want to see also
Frequently asked questions
Ampere's Law is a fundamental principle in physics that relates the magnetic field around a closed loop to the electric current passing through it. It states that the magnetic field produced by an electric current is directly proportional to the intensity of the current, with the constant of proportionality being the permeability of free space.
Ampere's Law can be used to calculate the magnetic field generated by a current-carrying wire. You would first need to draw an imaginary route encircling the wire at a certain distance. The line integral of the magnetic field along this path is equal to the current enclosed in the wire. Using the formula B = (μo x I) / L, where B is the magnetic field, μo is the permeability constant, I is the current, and L is the length of the loop, you can calculate the magnetic field.
While both laws deal with electromagnetism, they focus on different aspects. Ampere's Law relates the magnetic field to the electric current, while Faraday's Law of Electromagnetism focuses on the relationship between a changing magnetic field and the electric field it induces.
Ampere's Law has various applications, including calculating the magnetic field produced by a current-carrying wire, determining the magnetic field inside a conductor or a toroid, and calculating the force between two conductors.