In 1847, Gustav Kirchhoff extended Ohm's Law by developing a concept concerning the voltages contained in a series circuit loop. Known as Kirchhoff's Voltage Law, it states that the algebraic sum of the voltages in any closed path in a circuit is equal to zero. This law is particularly useful when dealing with complex circuits that include bridges or T networks, where Ohm's Law falls short. To apply Kirchhoff's Voltage Law, one must understand the meaning of voltage polarity and follow a systematic process that involves assigning polarities to voltages, placing correct polarities on sources, and tracing the circuit loop while noting voltage amounts and polarities. This law, along with Kirchhoff's Current Law, forms the basis for analysing lumped parameter circuits and enables systematic analysis of any electrical network.
| Characteristics | Values |
|---|---|
| What it is used for | Analysing the total voltage for a complex circuit |
| When it is used | When you can't use V = IR |
| When it is used | When you can't rely solely on Ohm's Law to find the voltage or current |
| When it is used | When you are building a complex circuit that includes bridges or T networks |
| What it states | The algebraic sum of the voltages in any closed path in a circuit is equal to zero |
| What it states | The algebraic sum of all voltage differences around any closed loop is zero |
| What it states | The sum of the voltage rises around a closed loop must equal the sum of the voltage drops around the loop |
| What it states | When going around a loop, you have to get back to the same voltage you started with |
| What it states | The total voltage will always equal the sum of all the voltage drops within the loop |
| How it works | You calculate the total resistance of the circuit |
| How it works | You calculate the total current of the circuit |
| How it works | You calculate the current through each resistor |
| How it works | You calculate the voltage drop across each resistor |
| How it works | You compare the voltage source to the total voltage drop to validate the law |
What You'll Learn

Understanding Kirchhoff's Voltage Law (KVL)
Kirchhoff's Voltage Law (KVL) is a fundamental principle in electrical engineering that allows for the analysis of complex electrical circuits. KVL, along with Kirchhoff's Current Law (KCL), forms the basis for understanding and designing lumped parameter circuits.
KVL is particularly useful when dealing with circuits that include bridges or T networks, where Ohm's Law falls short. While Ohm's Law is sufficient for calculating voltage, current, or resistance in a simple series or parallel circuit, KVL comes into play when the circuit becomes more intricate.
In 1847, G. R. Kirchhoff built upon Ohm's Law by formulating a simple concept regarding the voltages in a series circuit loop. KVL states that the algebraic sum of all voltage differences around any closed loop in a circuit is zero. In other words, the total voltage rises around a closed loop must equal the total voltage drops within the loop, ensuring the Conservation of Energy.
To understand KVL, it's important to grasp the concept of a loop. A loop is any closed path through the circuit that does not pass through the same node more than once. To create a loop, start at any node and trace a path until you return to that node.
Applying Kirchhoff's Voltage Law
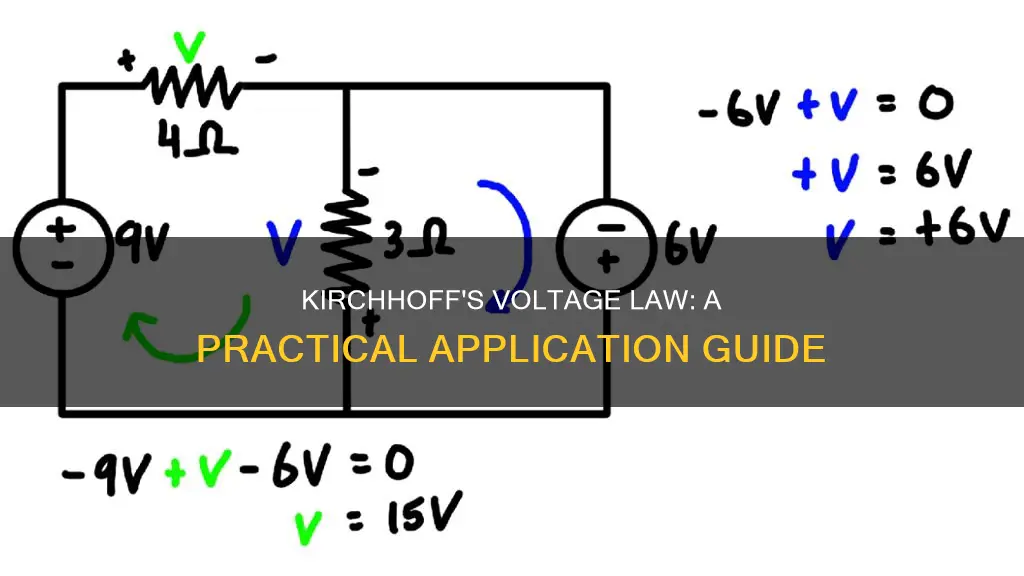
When applying KVL, it's essential to assume a direction of current flow through the circuit. This assumed direction doesn't need to be accurate, but it helps in assigning polarities to the voltages across the resistors. The positive and negative polarities are based on the direction of current flow.
Once the polarities are assigned, you can start at any point in the circuit and trace a loop. Write down the amount and polarity of the voltage across each component as you traverse the loop. The polarity of the voltage depends on whether the current passes through the component before or after reaching that point.
By placing these voltages and their polarities into an equation, you can solve for unknown values in the circuit. KVL provides a systematic approach to analysing complex electrical networks and finding voltages in circuits with both series and parallel resistance.
Example of Applying Kirchhoff's Voltage Law
Consider a circuit with three resistors connected across a 50-volt source. To find the voltage across the third resistor when the voltage drops across the first two resistors are 25 volts and 15 volts, respectively, follow these steps:
- Assume a direction of current flow and assign polarities to the resistors accordingly.
- Starting at any point, trace a loop in the circuit and record the voltage and polarity across each component.
- Write the equation for the loop, considering the amount and polarity of the voltages.
- Solve the equation to find the unknown voltage.
By applying KVL, you can analyse complex circuits and validate the law by comparing the voltage source to the total voltage drop.
Copyright Laws: Britain vs. USA
You may want to see also

Applying KVL to circuit analysis
Kirchhoff's Voltage Law (KVL) is a fundamental principle for circuit analysis. It states that for any closed-loop series path, the algebraic sum of all the voltages in a closed loop of a circuit is equal to zero. This is because a circuit loop is a closed conducting path, and as per the law of conservation of energy, no energy is lost.
Mathematically, Kirchhoff's Voltage Law can be written as ΣV = 0, where the term "algebraic sum" means taking into account the polarities and signs of the sources and voltage drops around the loop. This means that the positive and negative polarities of voltages must be assigned based on the direction of current flow.
To apply KVL to circuit analysis, follow these steps:
- Assume a direction of current flow: You can choose the direction of current flow to be either clockwise or anticlockwise. If you choose the wrong direction, the result will still be valid but will have a negative sign.
- Assign polarities to voltages: Using the assumed direction of current, assign positive and negative polarities to the voltages across all the resistors in the circuit.
- Place correct polarities on sources: Identify the voltage sources in the circuit and mark their polarities accordingly.
- Trace the circuit loop: Starting at any point in the circuit, trace around the loop in a chosen direction, noting the amount and polarity of the voltage across each component. When using arrows to indicate voltage polarities, remember that if the arrow direction matches the tracing direction, the voltage is positive; otherwise, it is negative.
- Set up the equation: Place the voltages and their polarities into an equation and solve for the desired quantity.
For example, consider a circuit with three resistors connected across a voltage source. To find the voltage across one of the resistors, you can apply KVL by assuming a current direction, assigning polarities, and then tracing the loop to write down the voltages. Substituting these values into the KVL equation will allow you to calculate the unknown voltage.
By applying KVL to circuit analysis, you can solve complex circuit problems that may be difficult or impossible to solve using Ohm's law alone. It provides a powerful tool for understanding and designing electrical circuits.
Exploring Natural Law Through the Lens of Metaethics
You may want to see also

Solving circuits with KVL
Solving circuits with Kirchhoff's Voltage Law (KVL) is a powerful tool for analysing complex circuits. KVL, developed by Gustav Kirchhoff in 1845, states that the sum of the voltages in any closed loop within a circuit is equal to zero. This law is particularly useful for series circuits.
To apply KVL, follow these steps:
- Understand Voltage Polarity: Before applying KVL, ensure you comprehend the concept of voltage polarity. In a circuit, the current flow direction determines the positive and negative polarities of the voltage. The end of a resistor where the current enters is marked positive, indicating a higher potential.
- Assume Current Direction: Assign a direction for the current flow in the circuit. While the correct direction is preferable, it is not mandatory. This step is crucial for defining voltage polarities.
- Assign Voltage Polarities: Using the assumed current direction, assign positive and negative polarities to the voltages across all components in the circuit. This step helps visualise voltage changes as the current flows.
- Trace the Circuit Loop: Starting at any point, trace the circuit loop in a chosen direction (clockwise or counterclockwise). Record the amount and polarity of the voltage across each component as you move along the loop. The voltage polarity is determined by the direction of the assumed current.
- Apply KVL Equation: Summing up the voltages around the closed loop, apply KVL's equation: the algebraic sum of voltages equals zero. Write down the equation and solve for the desired unknown values.
- Solve for Unknowns: Plug in the known voltage values and solve the equation to find the unknown voltages or currents in the circuit. This step may involve simultaneous equations and algebraic manipulations.
- Sanity Check: Review your solution to ensure the numbers make sense and are internally consistent. Check if the sum of voltage increases and decreases around the loop indeed equals zero.
By following these steps, you can effectively use KVL to solve complex circuits and determine unknown voltages and currents. KVL simplifies circuit analysis by breaking down the problem into manageable equations, making it a valuable tool in electrical engineering.
Are Churches Exempt from Accessibility Laws?
You may want to see also

KVL in AC circuits
Kirchhoff's voltage law (KVL) is a powerful tool for analysing electrical circuits, including AC circuits. KVL, along with Kirchhoff's current law (KCL), forms the basis of Kirchhoff's circuit laws, which help solve complex circuit problems by defining a set of basic network laws and theorems for voltages and currents.
KVL states that in any closed-loop network driven by a voltage source, the total voltage around the loop is equal to the sum of all the voltage drops within the same loop, which is equal to zero. In other words, the algebraic sum of all voltage sources and voltage drops within a closed loop must be zero since the algebraic sum of the voltage drops equals the algebraic sum of the voltage sources. This principle is known as the conservation of energy.
To apply KVL in AC circuits, the following steps can be followed:
- Start at any point in the loop and continue in the same direction, noting the direction of all voltage drops, whether positive or negative, and return to the starting point. Maintaining the same direction is crucial; otherwise, the final voltage sum may not be zero.
- When dealing with AC circuits, it is essential to consider the phase differences in the general equation for voltages across various components. At a particular time, regardless of the phase differences, there will be only one numeric value of voltage drop.
- By considering the series RLC circuit driven by an arbitrary voltage source, the canonical differential equation for the series current can be derived using KVL. This equation accounts for the voltage source, resistance, inductance, and capacitance in the circuit.
- KVL can be used in conjunction with Kirchhoff's Current Law (KCL) and Ohm's Law to solve complex circuit problems, especially in bridge or T networks, where Ohm's Law alone is insufficient.
- When analysing AC circuits using KVL, specific definitions and terminologies are employed, such as node, paths, branches, loops, and meshes. These terms are essential to understand as they are frequently used in circuit analysis.
- KVL assumes that the circuit follows ideal behaviour, and if this is not the case, KVL may not hold true. However, AC circuit analysis typically falls under the umbrella of ideal circuit theory, making KVL applicable.
Faraday's Law: Powering Generators with Electromagnetic Induction
You may want to see also

Practical considerations and limitations of KVL
Kirchhoff's Voltage Law (KVL) is a cornerstone of circuit analysis, but it's important to be aware of certain practical considerations and limitations that can impact its accuracy and applicability in real-world scenarios. Here are some key factors to keep in mind:
- Wire Resistance: In ideal KVL applications, wires are assumed to have zero resistance. However, in reality, wires do have resistance, and this can affect voltage measurements, especially in low-voltage or high-current circuits.
- Component Tolerances: Real-world components don't have perfect values. Resistors, capacitors, and inductors have tolerance ratings, which means their actual values can vary, leading to discrepancies in circuit analysis.
- Parasitic Elements: Components may exhibit parasitic inductance, capacitance, or resistance not accounted for in simple circuit models. These parasitic elements can significantly affect the behaviour of high-frequency AC circuits.
- Temperature Effects: The resistance of materials can change with temperature, impacting component values and circuit performance. This is particularly relevant for semiconductors and precision resistors.
- Nonlinear and Time-varying Components: KVL assumes linear and time-invariant elements within a circuit. Circuits with nonlinear components like diodes or transistors, or those with time-varying elements, require a more complex application of KVL and may demand additional analytical techniques.
- Electromagnetic Fields: KVL assumes a static magnetic field within a loop. However, in circuits with high inductance or rapid current changes, the induced voltages not accounted for by KVL can influence circuit behaviour.
- High-Frequency Circuits: At very high frequencies, the assumption of instantaneous voltage drops across components becomes less valid due to propagation delays and the wave nature of electrical signals.
- Applicability to AC Circuits: KVL is primarily designed for DC circuits. When applying it to AC circuits, you must consider reactance, impedance, and phase relationships, which introduce complexity due to the time-varying nature of AC signals.
Despite these considerations and limitations, KVL remains an essential tool in electrical engineering, especially when complemented with other analytical methods and a deep understanding of the underlying physical principles.
Applying to Harvard Law: Understanding the True Cost
You may want to see also







