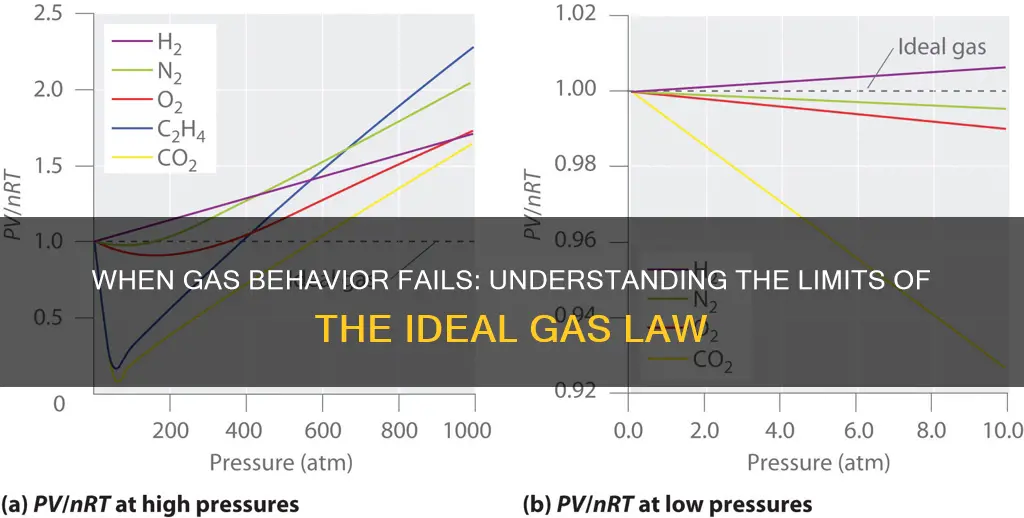
The ideal gas law is a fundamental equation in chemistry and physics that describes the behavior of gases under many conditions. However, it is essential to recognize that this law is an approximation and has limitations. When gases deviate from ideal behavior, the ideal gas law breaks down, and more complex equations of state are required to accurately describe the system. This occurs under certain conditions, such as high pressure, low temperature, or when gases contain large amounts of intermolecular forces or have a large molecular size. Understanding these conditions is crucial for accurate gas behavior predictions and the development of more sophisticated models.
| Characteristics | Values |
|---|---|
| Molecular Interactions | When gas molecules interact strongly with each other, the ideal gas law breaks down. This includes conditions where intermolecular forces become significant, such as at high pressures or low temperatures. |
| Real Gas Behavior | At high pressures and low temperatures, real gases deviate from ideal behavior. The gas molecules occupy a finite volume and have intermolecular attractions, leading to a compression factor that deviates from the ideal value of 1. |
| Condensation and Depletion | When gases condense into a liquid or solid state, the ideal gas law no longer applies. This occurs at pressures above the critical pressure and temperatures below the critical temperature. |
| Vapor Pressure and Boiling Point | The ideal gas law fails to account for the relationship between vapor pressure and boiling point. Real gases have a finite volume and intermolecular forces, which affect their phase transitions. |
| Deviations at Extreme Conditions | At extremely high pressures or low temperatures, the gas molecules are highly compressed and their kinetic energy is significantly reduced. This leads to deviations from ideal behavior, as the gas molecules occupy a smaller volume and experience stronger intermolecular forces. |
| Critical Points | The critical point is a specific temperature and pressure at which the distinction between liquid and gas phases disappears. Above this point, the gas law breaks down, and the gas cannot be liquefied, regardless of the pressure applied. |
What You'll Learn
- Molecular Interactions: When gas molecules interact strongly, the ideal gas law no longer applies
- High Pressures: At high pressures, gas molecules occupy a smaller volume, deviating from ideal behavior
- Low Temperatures: At low temperatures, quantum effects become significant, breaking the law's assumptions
- Non-Ideal Gases: Real gases deviate due to intermolecular forces, volume, and energy
- Condensation: When gases condense into liquids, the ideal gas law fails to predict this phase change

Molecular Interactions: When gas molecules interact strongly, the ideal gas law no longer applies
The ideal gas law is a fundamental equation in thermodynamics that describes the behavior of gases under certain conditions. It states that the product of the pressure (P) and volume (V) of a gas is directly proportional to the temperature (T) and the number of moles (n) of the gas, expressed as PV = nRT, where R is the gas constant. However, this law is based on the assumption that gas molecules do not interact with each other, allowing them to move freely and independently. When this assumption is violated, the ideal gas law breaks down, and the behavior of the gas becomes more complex.
Molecular interactions play a crucial role in determining when the ideal gas law fails. In an ideal gas, molecules are considered non-interacting, meaning they do not exert any significant force on each other. This allows for the assumption of point particles, where the volume occupied by the molecules is negligible compared to the volume of the container. However, in reality, gas molecules do possess volume and can interact through various forces, such as van der Waals forces or London dispersion forces.
When gas molecules interact strongly, the ideal gas law no longer holds. These interactions can lead to several deviations from ideal behavior:
- Deviations in Pressure and Volume: Strong molecular interactions can cause the gas molecules to occupy a larger volume than expected, leading to a decrease in pressure. This is because the molecules are attracted to each other, reducing their mobility and the frequency of collisions with the container walls. As a result, the gas takes up more space, and the pressure may be lower than predicted by the ideal gas law.
- Non-Ideal Enthalpy and Entropy: The enthalpy (internal energy) and entropy of a real gas can differ from those of an ideal gas. Strong interactions can lead to a more ordered arrangement of molecules, affecting the gas's entropy. Additionally, the internal energy of the gas may increase due to the potential energy associated with molecular attractions.
- Condensation and Phase Transitions: One of the most significant consequences of strong molecular interactions is the tendency for gases to condense into liquids or solids. When the intermolecular forces become dominant, the gas molecules can no longer remain in a gaseous state, leading to phase transitions. This is why the ideal gas law fails at very low temperatures or high pressures, where molecular interactions become significant.
Understanding these molecular interactions is essential in various fields, including chemistry, materials science, and engineering. It allows scientists and engineers to predict and explain the behavior of gases under different conditions, ensuring accurate calculations and predictions in real-world scenarios. By recognizing the limitations of the ideal gas law, researchers can employ more sophisticated models to describe the behavior of gases, especially in situations where molecular interactions are significant.
Ohio Child Breaks Federal Law: What's Next?
You may want to see also

High Pressures: At high pressures, gas molecules occupy a smaller volume, deviating from ideal behavior
At high pressures, the behavior of gases deviates significantly from the predictions of the ideal gas law, which assumes that gas molecules have negligible volume and exhibit no intermolecular forces. When gases are compressed to high densities, the assumptions of the ideal gas law no longer hold true. This is because, under such conditions, gas molecules are forced closer together, leading to increased interactions and a more complex behavior.
One of the key deviations at high pressures is the finite volume occupied by gas molecules. In the ideal gas law, PV = nRT, the volume (V) is considered to be the space occupied by the gas. However, at high pressures, the volume available for the molecules to move freely decreases, causing them to occupy a smaller space. This reduction in volume leads to an increase in the frequency of collisions between molecules, resulting in higher pressure than predicted by the ideal gas law.
The intermolecular forces also play a crucial role in the behavior of gases at high pressures. As the gas molecules are compressed, the attractive forces between them become more significant. These forces cause the molecules to slow down and occupy a more compact arrangement, deviating from the ideal assumption of random motion. The increased attraction can lead to a decrease in the gas's thermal energy, affecting its temperature and overall behavior.
Furthermore, at high pressures, the gas molecules may start to occupy a more ordered structure, forming a liquid-like state or even a solid-like arrangement. This is particularly true for gases with strong intermolecular forces, such as those containing hydrogen bonds or dipole-dipole interactions. The transition to a more ordered state further deviates the gas's behavior from the ideal gas law, which assumes a completely random and disordered arrangement of molecules.
In summary, at high pressures, the ideal gas law breaks down due to the finite volume occupied by gas molecules and the increased influence of intermolecular forces. These factors lead to deviations in pressure, temperature, and molecular arrangement, highlighting the limitations of the ideal gas law in describing the behavior of gases under extreme conditions. Understanding these deviations is essential for accurate predictions and calculations in various fields, including chemistry, physics, and engineering.
Steve Bannon: Legal Violations and Their Implications
You may want to see also

Low Temperatures: At low temperatures, quantum effects become significant, breaking the law's assumptions
At low temperatures, the behavior of gases deviates significantly from the predictions of the ideal gas law, which assumes that gas molecules are point masses with no volume and that their interactions are negligible. As the temperature decreases, the kinetic energy of the gas molecules diminishes, and their movement slows down. This reduction in kinetic energy leads to a decrease in the average distance between the molecules, causing them to occupy a smaller volume than what the ideal gas law predicts.
Quantum effects play a crucial role in this phenomenon. At very low temperatures, the principles of quantum mechanics become dominant, and the classical assumptions of the ideal gas law no longer hold. Quantum mechanics describes the behavior of particles at the microscopic level, where the wave-particle duality of matter becomes apparent. As the temperature approaches absolute zero, the gas molecules start to exhibit wave-like properties, and their behavior is governed by quantum wave functions.
The significant quantum effects at low temperatures include the formation of a Bose-Einstein condensate (BEC) in gases composed of bosons (particles with integer spin). Bosons can occupy the same quantum state, leading to a macroscopic quantum phenomenon. This behavior is in stark contrast to fermions (particles with half-integer spin), which cannot occupy the same quantum state due to the Pauli exclusion principle. At low temperatures, fermions form a Fermi gas, which also deviates from the ideal gas law.
The transition to a quantum state at low temperatures is a gradual process. As the temperature continues to decrease, the gas molecules occupy higher energy levels, and the quantum effects become more pronounced. This results in a decrease in the thermal conductivity and an increase in the viscosity of the gas, further deviating from the ideal gas behavior. Understanding these quantum effects is essential for accurately describing the properties of gases at extremely low temperatures, where classical physics fails to provide an accurate description.
Legal Consequences of Breaking the Law in Japan
You may want to see also

Non-Ideal Gases: Real gases deviate due to intermolecular forces, volume, and energy
The concept of non-ideal gases is crucial to understanding the limitations of the ideal gas law. Real gases deviate from ideal behavior due to various factors, primarily intermolecular forces, volume, and energy. These factors play a significant role in determining the gas's properties and behavior under different conditions.
Intermolecular forces, such as van der Waals forces, are weak attractions between gas molecules. These forces become significant when gas molecules are close together, which is more common at higher pressures or lower temperatures. At these conditions, the gas molecules experience an attractive force that reduces their kinetic energy and affects their behavior. For example, at high pressures, gas molecules are packed closer together, leading to increased intermolecular interactions and a deviation from ideal gas behavior.
Volume also contributes to the deviation from the ideal gas law. Real gases have a finite volume, meaning they occupy a specific space. In contrast, the ideal gas law assumes that gas molecules have no volume and occupy negligible space. When gas molecules have a finite volume, they can occupy the same space, leading to a phenomenon known as volume occupation. This effect becomes more pronounced at high pressures or low temperatures, where gas molecules are closer together and their volumes become more significant.
Energy considerations are another critical aspect of non-ideal gases. Real gases require more energy to be compressed or expanded compared to ideal gases. This is because intermolecular forces and volume effects require additional energy to overcome. For instance, when compressing a real gas, the gas molecules must overcome the attractive forces between them, which requires more energy than assumed in the ideal gas law. Similarly, when expanding a real gas, the molecules need to be separated, requiring additional energy to break the intermolecular interactions.
Understanding these factors is essential for accurate gas behavior predictions, especially in industrial processes and chemical engineering applications. Engineers and scientists can account for the deviations from ideal gas behavior by considering intermolecular forces, volume, and energy. This allows for more precise calculations and ensures the safe and efficient operation of various systems, such as those involving gas storage, transportation, and chemical reactions.
Coercion Tactics: Legally Threatening Someone
You may want to see also

Condensation: When gases condense into liquids, the ideal gas law fails to predict this phase change
The ideal gas law is a fundamental equation in thermodynamics, providing a simple and effective way to describe the behavior of gases under many conditions. However, it is important to recognize that this law has its limitations, and one of the key areas where it falls short is in predicting phase changes, particularly condensation. When a gas transitions into a liquid, the ideal gas law becomes inadequate, as it fails to account for the significant changes in molecular interactions and intermolecular forces.
Condensation is a process where the molecules of a gas come together and form a liquid. This phenomenon is observed when the temperature and pressure conditions are right for the gas to lose its gaseous state. As the gas molecules slow down and come into closer contact, they start to form a more ordered structure, which is characteristic of a liquid. The ideal gas law, however, assumes that gas molecules are widely spaced and move freely, with negligible intermolecular forces. When condensation occurs, the gas molecules are no longer free to move independently; they start to interact and form a more complex arrangement, which is not described by the ideal gas equation.
The breakdown of the ideal gas law during condensation can be understood through the concept of intermolecular forces. In a gas, these forces are relatively weak, allowing molecules to move freely and independently. As the gas transitions to a liquid, the intermolecular forces become stronger, leading to a more ordered and structured arrangement. This change in molecular interactions is not accounted for by the ideal gas law, which assumes a constant volume and ignores the effects of intermolecular attractions. As a result, the law fails to predict the correct behavior of the gas during condensation.
Furthermore, the ideal gas law does not consider the concept of surface tension, which plays a crucial role in the condensation process. Surface tension is the energy required to increase the surface area of a liquid, and it is influenced by the intermolecular forces between the liquid and its vapor. When condensation occurs, the gas molecules at the surface of the liquid experience an increase in intermolecular forces, leading to a reduction in the overall surface area. This phenomenon is not predicted by the ideal gas law, which treats the gas and liquid phases as separate and independent entities.
In summary, the ideal gas law breaks down when describing condensation due to its inability to account for the changes in molecular interactions and intermolecular forces. The law assumes a state of matter that is not representative of the complex and ordered structure formed during condensation. Understanding these limitations is essential for scientists and engineers to accurately predict and describe the behavior of gases and liquids in various conditions, especially when phase transitions occur.
Curbing CPS Overreach: Your Rights and Recourse
You may want to see also
Frequently asked questions
The Ideal Gas Law is a useful approximation for many gases under certain conditions, but it breaks down when gases deviate from ideal behavior. This typically occurs at high pressures and low temperatures, where the gas molecules occupy a significant volume and interact with each other, leading to deviations from the law's assumptions.
The law fails due to the effects of intermolecular forces, molecular size, and the presence of permanent dipoles or other polarizability. These factors become significant when gas molecules are close together, leading to deviations from the ideal behavior predicted by the law.
Under high-pressure conditions, the gas molecules are packed more closely together, and their interactions become more significant. This results in a deviation from the ideal gas law, as the volume occupied by the gas molecules themselves is no longer negligible, and the law's assumptions are no longer valid.
Yes, temperature plays a crucial role. At low temperatures, the kinetic energy of gas molecules decreases, and they may start to occupy a more significant volume due to quantum effects. This can lead to deviations from the ideal gas law, as the law assumes constant volume and temperature.
No, the law is most accurate for monatomic gases, which do not have intermolecular forces or molecular volume. For diatomic or polyatomic gases with permanent dipoles or other polarizability, the law may not hold, especially under conditions of high pressure and low temperature.







