Coulomb's law for magnets is an important concept in physics that describes the force of attraction and repulsion between two magnets. It is the magnetic equivalent of Coulomb's law for electric charges, formulated by 18th-century French physicist Charles-Augustin de Coulomb. Coulomb's law in the context of magnetism states that the force between two magnetic poles is directly proportional to the product of their pole strengths and inversely proportional to the square of the distance between them. This law helps explain the behaviour of magnets, which are objects that can attract other objects made of iron, steel, cobalt, and nickel, and are used in various applications such as toy trains, compasses, medical scans, and more.
What You'll Learn
- Magnets can be classified as naturally available or artificial
- The force of attraction or repulsion between two magnets is directly proportional to the product of their pole strengths
- The force is inversely proportional to the square of the distance between the magnets
- Magnetic Coulomb law is the magnetic equivalent of the electric Coulomb law
- Coulomb's law describes the force between magnetic poles

Magnets can be classified as naturally available or artificial
Magnets are objects that can attract other objects made of iron, steel, cobalt, and nickel, and they also produce a magnetic field. They are used in a variety of applications, from everyday items like toy trains and refrigerators to medical equipment such as MRI machines. Understanding the principles of magnetism is essential, and this is where Coulomb's Law comes into play.
Coulomb's Law of Magnetism describes the force of attraction and repulsion between two magnets. It states that the force between two magnetic poles is directly proportional to the product of their pole strengths and inversely proportional to the square of the distance between them. This law helps explain how magnets interact and is fundamental to understanding the behaviour of magnetic fields.
Now, magnets themselves can be classified based on two main criteria: their occurrence and their use. When it comes to occurrence, magnets can be categorized as either naturally available or artificial/man-made. Let's delve into these classifications:
Naturally Available Magnets
Lodestone, also known historically as magnetite, is the most well-known naturally occurring magnet. Other examples include pyrrhotite, columbite, and basalt. These magnets are formed through natural geological processes and were first discovered in a province in Asia called Magnetia. Naturally occurring magnets are relatively rare compared to artificial magnets, and they possess unique characteristics.
One of their distinctive features is their ability to retain magnetism indefinitely. Once magnetized, they do not require an external magnetic field to maintain their properties. This permanence is due to the alignment of their magnetic domains during formation. Additionally, natural magnets have irregular shapes, which limits their customization.
Artificial Magnets
Artificial magnets, on the other hand, are created by humans through various manufacturing processes. These include magnetization and electromagnetism. Common materials used for artificial magnets include iron, nickel, and cobalt alloys, such as neodymium magnets. By subjecting these materials to a magnetic field, they become magnetized and exhibit magnetic behaviour.
One advantage of artificial magnets is the ability to customize their shapes and sizes to suit specific applications. They can be molded into various forms, making them highly versatile. Artificial magnets are also known for their high magnetic strength, and their magnetism can be manipulated. They can be demagnetized and remagnetized by exposing them to different magnetic fields.
In summary, magnets can be classified as naturally available or artificial, each with its own distinct characteristics. Naturally available magnets, like lodestone, are formed through geological processes and retain their magnetism indefinitely. On the other hand, artificial magnets are human-made, customizable, and exhibit high magnetic strength. Understanding these classifications is essential in various scientific, technological, and industrial applications, as magnets play a crucial role in numerous aspects of our daily lives.
The Law and Black People: A Complex History
You may want to see also

The force of attraction or repulsion between two magnets is directly proportional to the product of their pole strengths
Coulomb's Law of Magnetism states that the force of attraction or repulsion between two magnets is directly proportional to the product of their pole strengths and inversely proportional to the square of the distance between them. This law is an important concept in physics, describing the interaction of magnetic poles and their resulting forces.
The mathematical representation of Coulomb's Law of Magnetism is:
F = K(m1m2) / μ0r^2
Where:
- F is the force between the magnets
- M1 and m2 are the strengths of the magnetic poles
- Μ0 is the permeability of free space
- R is the distance between the poles
This equation shows that as the product of the pole strengths increases, the force between the magnets also increases, assuming all other factors remain constant. The force decreases as the distance between the poles increases.
The force between magnets can be understood through the interaction of their magnetic fields, resulting in forces of attraction and repulsion. The magnetic field of each magnet is due to the movement of electrically charged electrons and the intrinsic magnetism of fundamental particles. These interactions can be modelled as tiny loops of current called magnetic dipoles, which produce their own magnetic fields.
The magnetic pole model further simplifies this concept by assuming that the pole surfaces of a magnet are covered in magnetic charges. In this model, the force between two magnets is predicted by Coulomb's Law, with magnetic charges instead of electric charges.
The alignment of molecular magnets within a magnet also plays a role in the force of attraction and repulsion. When two unequal magnetic poles attract, the alignment of molecular magnets in one magnet is supported by the other, resulting in a stronger force. Conversely, when two equal magnetic poles repel each other, the alignment of molecular magnets is disturbed, leading to a weaker force.
Animal Cruelty Laws: Do Farms Have Exemptions?
You may want to see also

The force is inversely proportional to the square of the distance between the magnets
Coulomb's Law of Magnetism is a fundamental concept in physics that explains the force of attraction and repulsion between two magnets. This law is similar to Coulomb's law in electrostatics, which describes the electric force between charged objects.
According to Coulomb's Law of Magnetism, the force between two magnetic poles is directly proportional to the product of their pole strengths and inversely proportional to the square of the distance between them. This relationship can be expressed mathematically as:
F = K (m1 * m2) / μ0r^2
Where F is the force, m1 and m2 are the strengths of the magnetic poles, r is the distance between the poles, K is a proportionality constant, and μ0 is the absolute permeability of free space (air or vacuum).
The inverse square relationship between force and distance means that as the distance between two magnets increases, the force between them decreases, and vice versa. In other words, the force between two magnets becomes weaker as they are moved farther apart and stronger as they are brought closer together.
This principle, often referred to as Coulomb's Inverse Square Law of Magnetism, is analogous to the behaviour of electric charges as described by Coulomb's Law in electrostatics. It is a fundamental concept in understanding the behaviour of magnetic fields and the forces between magnets.
The inverse square relationship between force and distance is a common theme in physics, appearing in various laws and equations, such as the law of universal gravitation and the intensity of light with distance. In the context of magnetism, this relationship helps explain the behaviour of magnets and their interactions, providing a quantitative framework for understanding and predicting the forces at play.
Civil Law and Private Colleges: Who Rules the Roost?
You may want to see also

Magnetic Coulomb law is the magnetic equivalent of the electric Coulomb law
Coulomb's Law, formulated by 18th-century French physicist Charles-Augustin de Coulomb, is a fundamental principle in physics that describes the electric force between charged objects. The law states that the magnitude of the attractive or repulsive force between two electrically charged particles is directly proportional to the product of their charges and inversely proportional to the square of the distance between them. This law is similar to Newton's inverse-square law of universal gravitation, but it accounts for both attraction and repulsion, depending on the charges of the objects.
The Magnetic Coulomb Law states that the force between the magnetic poles of two magnets is directly proportional to the product of their pole strengths and inversely proportional to the square of the distance between them. This law can be expressed mathematically as:
F = (μ0 / 4π) * (m1 * m2) / r^2
Where F is the force, m1 and m2 are the pole strengths, r is the distance between the poles, and μ0 is the permeability of free space.
In summary, the Magnetic Coulomb Law is a magnetic analogue of the electric Coulomb Law, with some distinctions arising from the unique characteristics of magnetic forces and the absence of magnetic monopoles in nature.
Antitrust Laws: Should NCAA Play by Different Rules?
You may want to see also

Coulomb's law describes the force between magnetic poles
Coulomb's Law, in its simplest definition, is an experimental law of physics that calculates the amount of force between two electrically charged particles at rest. The law was first published in 1785 by French physicist Charles-Augustin de Coulomb, and it states that the magnitude of the attractive or repulsive force between two charges is directly proportional to the product of the magnitudes of their charges and inversely proportional to the square of the distance between them.
Coulomb's Law can be applied to magnets. This is known as Coulomb's Law of Magnetism or the Magnetic Coulomb Law. This law describes the force of attraction and repulsion between two magnets. It states that the force of attraction or repulsion between two magnetic poles of suitable strengths (m1 and m2) held apart by a distance (r) is directly proportional to the product of their pole strengths and inversely proportional to the square of the distance between them.
The formula for Coulomb's Law of Magnetism can be expressed as:
F = K(m1m2) / μ0r^2
Where K is a constant, m1 and m2 are the strengths of the magnetic poles, r is the distance between the poles, and μ0 is the permeability of free space.
The force between the magnetic poles is also inversely proportional to the absolute permeability of the surrounding medium. This means that the force decreases as the distance between the poles increases, and the force is stronger when the poles are closer together.
It is important to note that, unlike electric charges, "magnetic charges" or magnetic monopoles do not exist in nature. However, with the use of tools like a long bar magnet, the force between the poles can be measured with reasonable accuracy.
Child Labor Laws: Volunteers Exempt or Included?
You may want to see also
Frequently asked questions
Coulomb's Law for magnets is analogous to Coulomb's Law for electric charges. It describes the force between magnetic poles and states that the force of attraction or repulsion between two magnets is directly proportional to the product of their pole strengths and inversely proportional to the square of the distance between them.
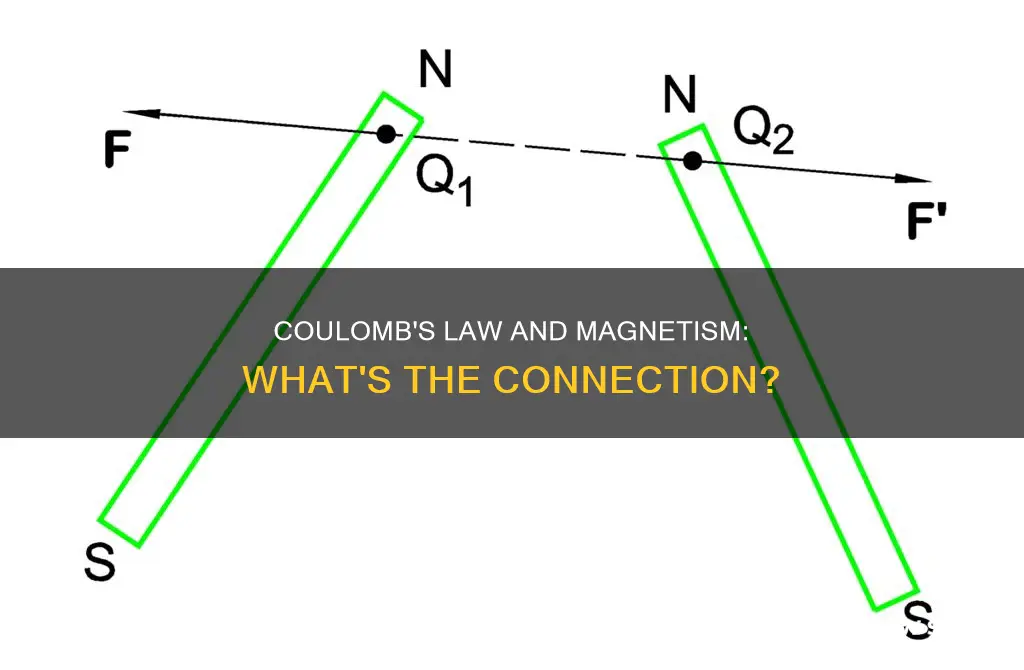
An important difference is that, unlike electric charges, "magnetic charges" (magnetic monopoles) do not exist in nature. Another difference is that there are two common measures of the "amount of magnetism" in SI units, namely the magnitudes of Q1 and Q2, due to the two vector fields giving the magnetic force.
The formula for Coulomb's Law for magnets is F = K (m1m2) / μ0r2, where K is a constant, m1 and m2 are the strengths of the magnetic poles, μ0 is the permeability of free space, and r is the distance between the poles.
A practical example of the Coulomb force in magnets is static cling. In dry winter air, garments made of synthetic material collect a charge. A plastic or rubber comb passed through the hair also becomes charged and will pick up bits of paper.







