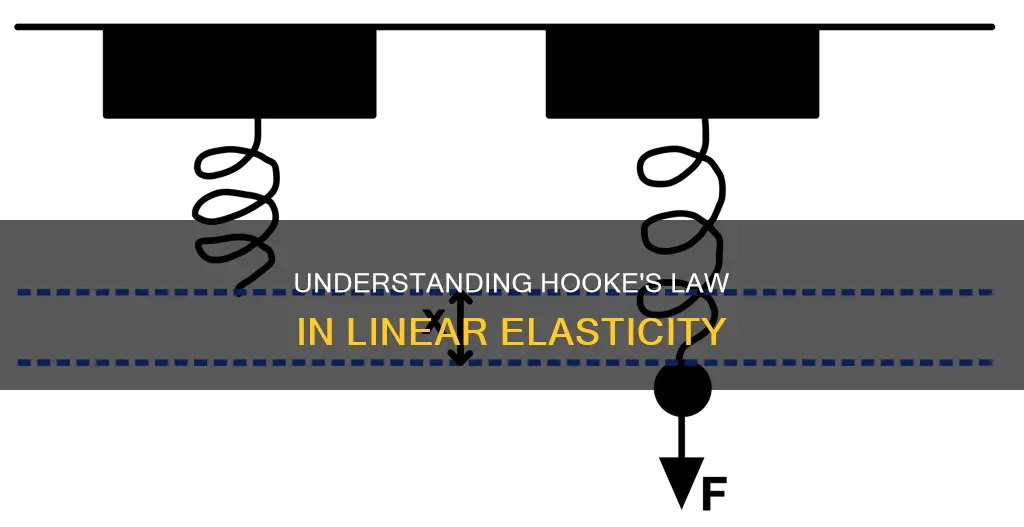
Hooke's law, an empirical law of physics, states that the force required to extend or compress a spring is directly proportional to the displacement or change in length. This principle, discovered by 17th-century British physicist Robert Hooke, is expressed mathematically as F = kx, where F is the force and k is a constant indicative of the spring's stiffness. Hooke's law is a foundational principle in various scientific and engineering fields, including seismology, molecular mechanics, and acoustics, and it is applicable to a wide range of situations beyond springs, such as the deformation of elastic bodies like rubber bands and balloons. However, it is important to note that Hooke's law is only an approximation and may deviate for certain materials or when forces exceed certain limits.
| Characteristics | Values |
|---|---|
| Law named after | 17th-century British physicist Robert Hooke |
| First stated | In 1660 as a Latin anagram |
| Published solution | In 1678 as "ut tensio, sic vis" |
| Translation | "As the extension, so the force" or "the extension is proportional to the force" |
| Equation | F = kx |
| F | Applied force |
| k | Constant or spring constant |
| x | Displacement or change in length |
| Compatibility with Newton's laws of static equilibrium | Yes |
| Compatibility with First Law of Thermodynamics | Yes |
| General form | Compatible with Newton's laws of static equilibrium |
| Modern theory of elasticity | Generalized variation of Hooke's law |
| Stress | Force on unit areas within a material |
| Strain | Relative deformation produced by stress |
What You'll Learn

Hooke's Law and linear elasticity
Hooke's law, F = kx, states that the force (F) needed to extend or compress a spring by some distance (x) is directly proportional to that distance. The law is named after 17th-century British physicist Robert Hooke, who formulated it in 1660 and published the solution in 1678. The value of the constant k depends on the type of elastic material, its dimensions, and its shape.
Hooke's law is a first-order linear approximation of how springs and other elastic bodies respond to applied forces. It holds (to some extent) in many situations where an elastic body is deformed, such as when wind blows on a tall building or a musician plucks a guitar string. An elastic body or material that follows this equation is said to be linear-elastic or Hookean.
The modern theory of elasticity generalizes Hooke's law, stating that the strain (deformation) of an elastic object or material is proportional to the stress applied to it. This generalized version of Hooke's law applies to continuous media, where the stresses and strains within a material are connected by a linear relationship.
Hooke's law is only accurate for small forces and deformations. It eventually fails when forces exceed a certain limit, as no material can be compressed beyond a minimum size or stretched beyond a maximum size without permanent deformation. Many materials will deviate noticeably from Hooke's law before these elastic limits are reached.
However, Hooke's law is a good approximation for most solid bodies, as long as the forces involved are small. It is extensively used in all branches of science and engineering and is the foundation of disciplines such as seismology, molecular mechanics, and acoustics. It also has practical applications, such as in the creation of the balance wheel, which made mechanical clocks, portable timepieces, spring scales, and manometers possible.
Black Holes: Beyond the Laws of Physics?
You may want to see also

Stress and strain
Strain, on the other hand, describes the deformation caused by stress. It is given as a fractional change in length under tensile stress, volume under bulk stress, or geometry under shear stress. Strain is a dimensionless number, meaning it does not have any units. Similar to stress, different types of strain are categorised based on the type of stress causing the deformation. For instance, tensile strain occurs when there is a fractional change in length, while bulk strain or volume strain happens when there is a change in volume.
The relationship between stress and strain is not always linear. The deformation caused by stress is directly proportional to the stress value only when the stress is sufficiently low. This proportionality constant in the relation between stress and strain is called the elastic modulus. The elastic modulus has the same physical unit as stress because strain is dimensionless.
Hooke's law, an empirical law in physics, states that the force needed to extend or compress a spring by some distance scales linearly with that distance. In other words, the applied force is proportional to the displacement or change in length. This law applies to various situations where an elastic body is deformed, such as a wind blowing on a tall building or a musician plucking a guitar string. An elastic body that follows this equation is said to be linear-elastic or Hookean.
Hooke's law can be applied to understand the stress-strain relationship in materials that exhibit linear elasticity. In the context of stress and strain, Hooke's law states that stress is proportional to strain for small deformations. This means that as long as the stress is sufficiently low, the deformation of the material will be directly proportional to the applied stress.
However, it is important to note that Hooke's law is only a first-order linear approximation and may not hold for larger forces or deformations. Many materials may deviate from Hooke's law even before reaching their elastic limits. Therefore, Hooke's law accurately describes the stress-strain relationship in the linear elastic region, where the material undergoes only elastic deformation and returns to its original shape when the force is removed.
Grahams Law: Ideal Gases and Beyond
You may want to see also

Elastic behaviour of solids
Elastic behaviour in solids refers to the ability of a solid body to return to its original shape and size after deforming forces are removed. This is also known as the body's elasticity.
Elasticity is an idealisation, as no material is perfectly elastic. All materials have an elastic limit, beyond which they will start to lose their ability to exhibit perfect elastic behaviour and undergo plastic deformation. Plastic deformation is non-reversible and permanent.
At the atomic level, solids are made up of atoms or molecules surrounded by other atoms or molecules, which are held in a state of equilibrium by interatomic forces. When an external force is applied, these particles are displaced, resulting in the deformation of the solid. The displacement causes fixed points to vary, resulting in changes in interatomic and intramolecular distances. This can be observed in the example of a slingshot, which deforms when stretched but returns to its original shape when the force is removed.
The elastic limit varies depending on the type of solid. For example, a steel bar or wire may only be stretched by around 1% of its original length, whereas certain rubber-like materials can be stretched by up to 1,000%.
The elastic behaviour of solids is critical in engineering design. For example, understanding the elastic properties of materials such as steel and concrete is essential when designing buildings, bridges, automobiles, and other structures.
There are three mechanical properties that explain the elastic behaviour of solids: deformation, deforming force, and restoring force. Deformation refers to the change in the solid's shape due to force or stress. The deforming force is the outside force responsible for this change. The restoring force acts in the opposite direction to the deforming force and helps the solid to restore its shape once the outside force is removed.
In summary, the elastic behaviour of solids depends on several factors, including the deforming force, the solid's elastic limit, and its mechanical properties.
Laws and Regulations for PWC Operators: What You Need Know
You may want to see also

The spring constant
For example, in the design of a car suspension system, the spring constant is crucial for determining the force a spring can withstand and the amount of deflection expected under a given weight. A higher value of k indicates a stiffer spring, which requires more force to produce a given displacement. This characteristic is essential when control over motion and force is necessary, such as in shock absorbers.
In summary, the spring constant is a fundamental concept in understanding and designing spring-based systems. It provides a quantitative measure of spring stiffness and enables engineers to optimise and troubleshoot mechanical systems that rely on springs to function effectively and safely.
HIPAA Laws: Do They Apply to Veterinary Practices?
You may want to see also

The modern theory of elasticity
The theory of elasticity is concerned with the mechanics of deformable bodies and how they respond to applied forces. It treats the relationship between the forces exerted on an object and the resulting deformations. In practice, this often involves studying simple deformations, such as uniaxial elongation, simple shear, and uniform compression, to determine the corresponding elastic constants.
Elasticity is the ability of a body to resist distortion and return to its original state once the force is removed. This is in contrast to plasticity, where the object remains in its deformed state. The theory of elasticity helps us understand this behaviour and predict how objects will respond to applied forces, making it a valuable tool in engineering and design.
The elasticity of a material can be quantified using elastic moduli such as Young's modulus, the bulk modulus, or the shear modulus. These moduli measure the amount of stress needed to achieve a unit of strain, with higher moduli indicating that the material is harder to deform.
While Hooke's law provides a good approximation for most solid bodies when the forces and deformations are small, the modern theory of elasticity offers a more comprehensive understanding of elastic behaviour by generalising Hooke's law and applying it to more complex situations.
Retroactive Law Application: Litigation's Impact Explored
You may want to see also
Frequently asked questions
Hooke's Law is a principle of physics that states that the force required to extend or compress a spring by a certain distance is proportional to that distance. The law was formulated by 17th-century British physicist Robert Hooke, who aimed to demonstrate the relationship between the force applied to a spring and its elasticity.
The equation for Hooke's Law is F = kx, where F is the force applied to the spring, x is the displacement of the spring, and k is the spring constant, which indicates the stiffness of the spring.
Hooke's Law has numerous applications. It is used in the creation of automotive suspension systems, pendulum clocks, mechanical clocks, portable timepieces, spring scales, manometers, and pressure gauges. It also serves as a foundation for various scientific disciplines, including seismology, molecular mechanics, and acoustics.







