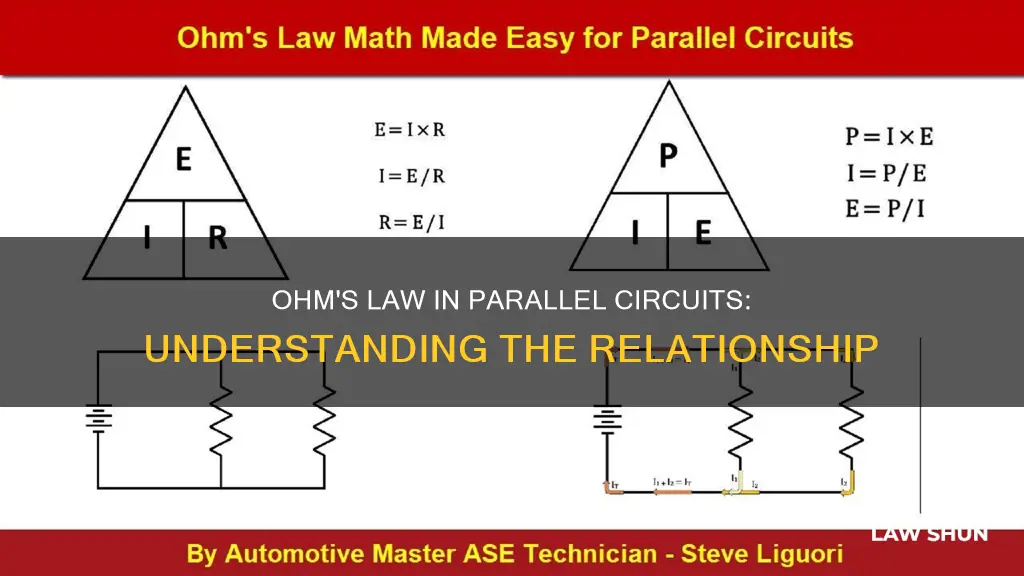
Ohm's Law is a formula used to determine how voltage, current, and resistance in an electrical circuit relate to one another. It was named after Georg Ohm, who discovered that current flow through a conductor is directly related to voltage and resistance. The formula is expressed as V = I x R, R = V/I, and I = V/R, where V stands for voltage, I for current, and R for resistance. When applying Ohm's Law to complex series and parallel circuits, it is important to remember that the variables used in the equations must be common to the same two points in the circuit under consideration. This is a common mistake made by beginners, who might mix the contexts of voltage, current, and resistance.
| Characteristics | Values |
|---|---|
| Voltage | The voltage is the same for all components in a parallel circuit |
| Current | The total parallel circuit current is the sum of the individual branch currents |
| Resistance | The total resistance of a parallel circuit is less than any of the individual branch resistances |
What You'll Learn

Ohm's Law and voltage in parallel circuits
Ohm's Law is a formula used to determine how voltage, current, and resistance in an electrical circuit relate to one another. It was named after Georg Ohm, who discovered that current flow through a conductor is directly related to voltage and resistance.
Ohm's Law can be applied to both series and parallel circuits, but it is important to understand the differences between the two types of circuits. In a series circuit, the total resistance is the sum of the individual resistances and is, therefore, always greater than any of the resistors individually.
In contrast, a parallel circuit has several different paths for electricity to travel, and the total resistance is not equal to the sum of the resistors. Instead, the total resistance in a parallel circuit is always less than any of the individual branch resistances. As more parallel resistors are added to the circuit, the total resistance decreases, and the total current increases because Ohm's Law states that lower resistance results in higher current.
The voltage in a parallel circuit is the same across each component, and the total current is the sum of all the individual branch currents. To calculate the total resistance in a parallel circuit, the formula is:
$R_{total} = \frac{1}{\frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}}$
This formula demonstrates that the total resistance in a parallel circuit is inversely proportional to the sum of the reciprocals of the individual resistances.
When applying Ohm's Law to complex series and parallel circuits, it is important to remember that the variables used in the equations must be common to the same two points in the circuit under consideration. Mixing the contexts of voltage, current, and resistance is a common mistake that can lead to incorrect results.
By following these guidelines and using the appropriate formulas, Ohm's Law can be effectively applied to parallel circuits to determine voltage, current, and resistance values.
Lease-Option Transactions: Confirmation Laws Applicable?
You may want to see also

Ohm's Law and current in parallel circuits
Ohm's Law is a formula used to determine how voltage, current, and resistance in an electrical circuit relate to one another. The law is named after Georg Ohm, who discovered the direct relationship between current flow in a conductor and voltage and resistance.
Ohm's Law can be applied to both series and parallel circuits, but it is important to understand the differences between the two types of circuits. A parallel circuit has two or more paths for the electricity to flow, and the loads are parallel to each other. If one of the parallel paths is broken, the current will continue to flow through the other paths.
In a parallel circuit, the voltage is the same across all components, and the total current is the sum of all the individual branch currents. This can be calculated using the equation:
$$I_{total} = I_{R1} + I_{R2} + I_{R3} + ...$$
Where $I_{total}$ is the total current and $I_{R1}$, $I_{R2}$, etc. are the currents in each branch.
The total resistance in a parallel circuit is less than any of the individual branch resistances. As more parallel resistors are added, the total resistance decreases. The formula for calculating the total resistance in a parallel circuit is:
$$R_{total} = \frac{1}{\frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + ...}$$
Where $R_{total}$ is the total resistance and $R_1$, $R_2$, etc. are the resistances in each branch.
It is important to note that when applying Ohm's Law to complex series and parallel circuits, the variables used in the equations must be common to the same two points in the circuit under consideration. This means that when calculating a variable for a single component, the voltage, current, and resistance values must be specific to that component only.
By following these principles and using Ohm's Law, we can analyze and solve for unknown values in parallel circuits.
Marsy's Law: Rights for Victims of Impaired Driving Accidents?
You may want to see also

Ohm's Law and resistance in parallel circuits
Ohm's Law states that the voltage across a conductor is directly proportional to the current flowing through it, provided that the physical conditions and temperature remain constant. In other words, it defines the relationship between voltage, current, and resistance in a circuit.
Now, in a parallel circuit, there are multiple paths for the current to flow through. Each path, or branch, has its own individual resistance, and these resistors are said to be connected in parallel. The key principles of a parallel circuit are:
- Voltage: The voltage is equal across all components in a parallel circuit.
- Current: The total circuit current is the sum of the individual branch currents.
- Resistance: The total resistance of a parallel circuit is less than any of the individual branch resistances.
Ohm's Law can be applied to each branch of a parallel circuit to determine the current flowing through it, given that the voltage and resistance are known.
To calculate the total resistance of a parallel circuit, the reciprocal of the individual resistances are added together, and the inverse of this sum gives the equivalent resistance.
Mathematically, the relationship between total resistance and individual resistance in a parallel circuit is:
$$R_{total} = \frac{1}{\frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}}$$
This formula demonstrates that the total resistance of a parallel circuit is always less than the smallest individual resistance in the circuit.
In summary, Ohm's Law can be applied to each branch of a parallel circuit to determine the current, and it can also be used to calculate the total resistance of the entire parallel circuit.
Laws of Motion: Space Edition
You may want to see also

Ohm's Law and conductance in parallel circuits
Ohm's Law is a formula used to determine how voltage, current, and resistance in an electrical circuit relate to one another. It is named after Georg Ohm, who discovered that current flow through a conductor is directly related to voltage and resistance.
Ohm's Law can be applied to both series and parallel circuits, but it is important to understand the differences between these two types of circuits. A parallel circuit has two or more paths for the electricity to flow, and the loads are parallel to each other. If one of the parallel paths is broken, the current will continue to flow through the other paths.
The voltage in a parallel circuit is the same across each component, and the total current is the sum of all the individual branch currents. The total resistance of a parallel circuit is less than any of the individual branch resistances, and it can be calculated using the following formula:
$$R_{total} = \frac{1}{\frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}}$$
This formula shows that the total resistance of a parallel circuit is not simply the sum of the individual resistors, as it is in a series circuit. Instead, each parallel resistor added to the circuit reduces the total equivalent resistance.
When applying Ohm's Law to a parallel circuit, it is important to remember that the variables used in the equations must be common to the same two points in the circuit under consideration. This means that when calculating a variable for a single component, you must ensure that the voltage, current, and resistance values are specific to that component only.
Additionally, when calculating the total power in a parallel circuit, it is important to sum the power dissipated by all the components. This can be done using the formula:
$$P_{total} = P_1 + P_2 + P_3$$
By following these guidelines and using the correct formulas, Ohm's Law can be effectively applied to parallel circuits to determine the voltage, current, resistance, and power in the circuit.
Zoning Laws: Do They Affect Your Web Store?
You may want to see also

Ohm's Law and power in parallel circuits
Ohm's Law states that the voltage across a conductor is directly related to the current and resistance. In other words, the voltage can be found by multiplying the current and resistance in a circuit or component.
Now, when it comes to applying Ohm's Law to parallel circuits, it's important to understand the fundamental characteristics of such circuits. In a parallel circuit, all components share the same electrical nodes. As a result, the voltage across each component remains the same. However, the total current in the circuit is the sum of the individual branch currents. This is because, in a parallel circuit, the total resistance is less than any of the individual branch resistances.
Let's consider an example to illustrate this. Suppose we have a parallel circuit with three resistors, R1, R2, and R3, connected to a single battery. If the voltage across the battery is 9V, and the resistances of the three resistors are 10kΩ, 2kΩ, and 1kΩ, respectively, we can use Ohm's Law to find the current through each resistor:
- For R1: I_R1 = V/R1 = 9V/10kΩ = 0.9mA
- For R2: I_R2 = V/R2 = 9V/2kΩ = 4.5mA
- For R3: I_R3 = V/R3 = 9V/1kΩ = 9.0mA
Now, to find the total current in the circuit, we sum up the individual branch currents:
Itotal = I_R1 + I_R2 + I_R3 = 0.9mA + 4.5mA + 9.0mA = 14.4mA
So, the total current in the parallel circuit is 14.4mA.
To calculate the total power in a parallel circuit, we can use the formula:
Ptotal = Vtotal Itotal
Where Vtotal is the total voltage, and Itotal is the total current.
It's important to note that when applying Ohm's Law, the variables of voltage, current, and resistance must be specific to the component or set of components under consideration. Mixing contexts can lead to incorrect results.
Agency Law: Slip and Fall Incidents - Who's Liable?
You may want to see also
Frequently asked questions
Ohm's Law states that the voltage across a circuit is equal to the product of the current flowing through it and the resistance it encounters. In a parallel circuit, the voltage is the same across all components, and the total current is the sum of all individual branch currents. The total resistance of a parallel circuit is less than that of any individual branch resistance.
The total resistance (Rt) in a parallel circuit can be calculated using the formula:
1/Rt = 1/R1 + 1/R2 + 1/R3 + ...
Where R1, R2, etc. are the resistances of the individual branches.
To calculate the total current in a parallel circuit, first, find the total resistance (Rt) using the formula above. Then, apply Ohm's Law:
Itotal = Voltage/Rt