Kirchhoff's Voltage Law, also known as Kirchhoff's Second Law, is a fundamental principle in circuit analysis. This law, formulated by German physicist Gustav Kirchhoff in 1845 (or 1847, according to some sources), states that the algebraic sum of all voltage differences around any closed loop in a circuit is equal to zero. In other words, the sum of the voltage rises around a closed loop is equal to the sum of the voltage drops, and you end up back at the same voltage you started with. This principle is based on the concept of a loop, which is any closed path through the circuit that does not pass through the same node more than once. Kirchhoff's Voltage Law can be applied to series circuits to analyse and calculate the voltages and currents within the circuit.
| Characteristics | Values |
|---|---|
| What Kirchhoff's Voltage Law States | The algebraic sum of all voltage differences around any closed loop is zero. |
| Another Way to State Kirchhoff's Voltage Law | The sum of the voltage rises around a closed loop must equal the sum of the voltage drops around the loop. |
| The Direction of Current Flow | The direction of current flow around a closed circuit can be assumed to be either clockwise or anticlockwise. |
| The Importance of Direction | It is important to maintain the same direction (either clockwise or anti-clockwise) or the final voltage sum will not be equal to zero. |
| Application of Kirchhoff's Voltage Law | Kirchhoff's Voltage Law can be applied to analyse series circuits. |
What You'll Learn

Understanding Kirchhoff's Voltage Law (KVL)
Kirchhoff's Voltage Law (KVL) is a fundamental principle in circuit analysis, discovered by German physicist Gustav Kirchhoff in 1847. KVL is particularly useful when dealing with series circuits and voltage divider circuits.
The Law
KVL states that the algebraic sum of all voltage differences around any closed loop in a circuit is zero. In other words, the sum of the voltage rises around a closed loop is equal to the sum of the voltage drops, and this property of Kirchhoff's law is known as the conservation of energy.
Applying KVL
When applying KVL, it is important to understand voltage polarity. The direction of the polarity and the sign of the voltage drop across a resistive element depend on the direction of the current flowing through it. As a general rule, you will lose potential in the same direction as the current across an element and gain potential as you move in the direction of an EMF source.
When using KVL, you can choose the direction of the current flow around a closed circuit as either clockwise or anticlockwise. If the chosen direction is different from the actual direction of the current flow, the result will still be correct but will have a negative sign.
Example
Let's consider a simple example of a series circuit with a 45-volt battery and three resistors. We will number the points in the circuit for voltage reference.
If we connect a voltmeter between points 2 and 1, the meter will register +45 volts. Now, if we measure the voltage drop across each resistor, stepping around the circuit in a clockwise direction, we will obtain the following readings:
- Between points 2 and 3: -15 volts
- Between points 3 and 4: -15 volts
- Between points 4 and 1: -15 volts
The sum of the voltage drops across the resistors equals 45 volts, which is the same as the battery's output. However, the polarity of the battery's output is opposite to that of the resistor voltage drops, resulting in a net voltage of 0 volts measured across the entire circuit.
KVL in Complex Circuits
Kirchhoff's Voltage Law can also be applied to complex circuits to determine unknown voltages. For example, consider two series circuits joined by a single wire. If we want to find the voltage between points 3 and 4, we can set up a KVL equation and step around the loop, recording the voltage drop figures.
By solving the KVL equation, we can determine the unknown voltage between points 3 and 4.
HIPAA Laws: Do They Apply to the Deceased?
You may want to see also

Applying KVL to a series circuit
Kirchhoff's Voltage Law (KVL) is a fundamental principle in circuit analysis, stating that the algebraic sum of all voltage differences around any closed loop in a circuit is zero. This law is based on the concept of a loop, which is any closed path through a circuit that does not pass through a node more than once.
When applying KVL to a series circuit, it is crucial to understand the direction of the current and the polarity of the voltage drops across the circuit elements. Here are the steps to apply KVL to a series circuit:
- Understand the Direction of Current: Determine the direction of current flow in the circuit. This can be assumed to be either clockwise or anticlockwise. While the chosen direction may differ from the actual current flow, it will not affect the validity of the result, only the algebraic sign.
- Assign Polarities: Assign positive and negative polarities to the voltages across the circuit elements, such as resistors, based on the direction of current flow. The voltage drop across a resistor will depend on the direction of current flow relative to the resistor terminals.
- Consider Voltage Sources: If there are any voltage sources in the circuit, such as batteries, assign the appropriate polarities to them as well.
- Choose a Starting Point: Select any point in the circuit as the starting point for your loop.
- Trace the Loop: Starting from the chosen point, trace a path through the circuit, encountering each node only once, and return to the starting point. Pay attention to the direction of traversal and note all voltage drops and their polarities along the way.
- Apply KVL Equation: Write down the KVL equation by summing up all the voltage differences around the loop, considering their polarities. The sum of these voltages should equal zero.
- Solve for Unknowns: If there are unknown voltages or currents in the circuit, you can set up and solve equations using KVL to determine their values.
By following these steps, you can apply KVL to analyse series circuits and calculate unknown values. KVL is a powerful tool for understanding and solving complex circuit problems, providing insights into the conservation of energy within the circuit.
The Physics of Other Worlds Explained
You may want to see also

The algebraic sum of voltages in a loop
Kirchhoff's Voltage Law (KVL) is a fundamental principle in circuit analysis, stating that the "algebraic sum of all voltages in a loop must equal zero". This law was formulated by German physicist Gustav Kirchhoff in 1845 or 1847 and is particularly useful for analysing series circuits.
The "algebraic sum" refers to accounting for both the magnitudes and polarities (or signs) of the voltages. A "loop" refers to any path traced from one point in a circuit to other points and back to the initial point. This can be understood as a closed loop or circuit, where you end up back at the same point with the same initial potential, and no energy or voltage loss.
To apply KVL, you can start at any point in the circuit and move in any direction, as long as you return to the starting point. The polarities of the voltages are based on assumed voltage difference polarities, and as long as these directions are consistent, the final result will reflect the actual voltage polarities in the circuit. This is because, while the direction chosen might differ from the actual direction of current flow, the result will still be correct, but with the algebraic answer having a minus sign.
For example, in a simple series circuit, you can measure the voltage drop across each resistor, stepping around the circuit in a clockwise direction. The polarities of the resistor voltage drops will be opposite to that of the battery. This is because the resistors are resisting the flow of electric charge being pushed by the battery. So, the "push" exerted by the resistors is in the opposite direction of the electromotive force.
In a more complex circuit, KVL can be used to determine an unknown voltage when all other voltages around a particular "loop" are known. For instance, in a circuit with two series circuits joined by a single wire, you can set up a KVL equation to find the voltage between two points by stepping around the loop and writing down the voltage drop figures.
Understanding ADA Laws: Private Business Obligations
You may want to see also

Tracing a loop in a circuit
To trace a loop, begin at any node in the circuit and follow a path through the circuit until you return to the starting node. This path can be traversed in either a clockwise or anticlockwise direction, but it is crucial to maintain consistency in the chosen direction to ensure accurate calculations.
For example, let's consider a simple circuit with nodes labelled a, b, c, d, and e. There are three possible loops in this circuit: a-b-e-d-a, a-b-c-e-d-a, and b-c-e-b. By applying KVL to each of these loops, we can analyse the voltage differences and polarities within the circuit.
When applying KVL, it is important to assign polarities to the voltage differences in the loop. The assumed directions of the voltages should be consistent from loop to loop to ensure accurate results. By following this convention, we can determine the voltage polarities and calculate the algebraic sum of voltage differences around each loop, which should always equal zero according to KVL.
In conclusion, tracing a loop in a circuit involves starting at any node and following a closed path back to the same node while considering the direction and voltage polarities to accurately apply Kirchhoff's Voltage Law.
Jones Law: Understanding Its Application in USVI
You may want to see also

Using KVL to find unknown voltages
Kirchhoff's Voltage Law (KVL) is a fundamental principle in circuit analysis, discovered by German physicist Gustav Kirchhoff in 1847. It states that the algebraic sum of all voltages in a closed loop series path is equal to zero. This is because a circuit loop forms a closed conducting path, and therefore, no energy is lost.
When applying KVL, it is crucial to consider the polarities and signs of the voltage sources and drops around the loop. The direction of the loop can be chosen arbitrarily, but it must be maintained consistently throughout the analysis. The voltage polarities in the loop are based on assumed directions, and as long as these assumptions are consistent, the final result will reflect the actual voltage polarities.
To find unknown voltages using KVL, we can set up equations that represent the closed loop and solve for the unknown voltage. Here's a step-by-step guide:
- Identify the Loop: Start at any node in the circuit and trace a path through the circuit until you return to the starting node. This forms a closed loop.
- Assign Polarities: Assign positive and negative polarities to the voltage sources and drops around the loop. This can be done based on the assumed directions of the voltages.
- Apply KVL Equation: Write the KVL equation for the loop, summing up all the voltages around it. The algebraic sum of these voltages must equal zero.
- Solve for Unknown Voltage: If there is an unknown voltage in the loop, you can set up an equation with that voltage as the unknown and solve for its value.
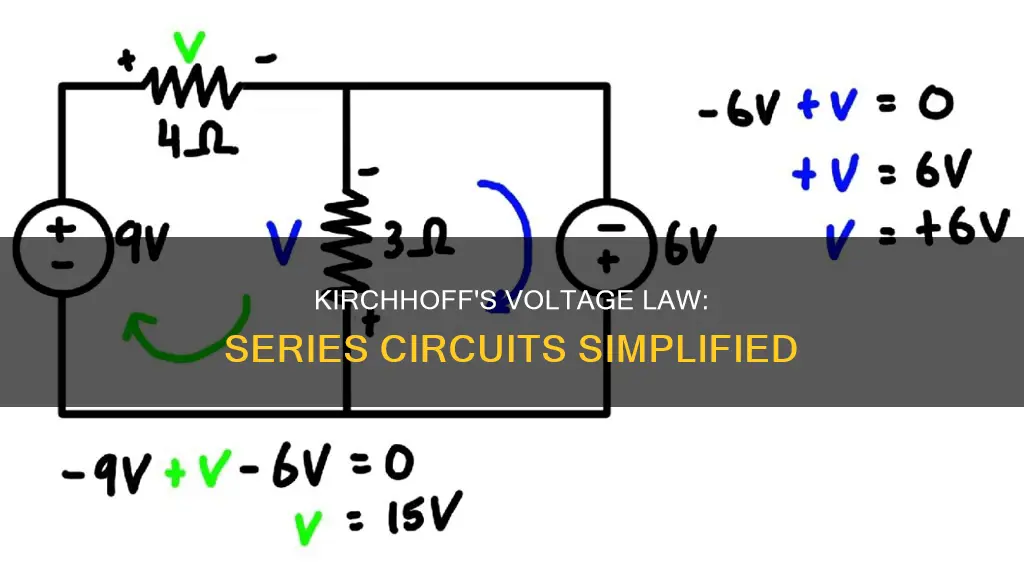
For example, consider the following series circuit:

To find the unknown voltage drop across the 4-ohm resistor, we can apply KVL to the loop:
- Assign positive polarity to the left side of the voltage source and negative polarity to the right side.
- The voltage drop across the 2-ohm resistor is negative since current flows from positive to negative.
- The voltage drop across the 4-ohm resistor is unknown and denoted as 'V'.
- The voltage drop across the 6-ohm resistor is positive since current flows from negative to positive.
Applying KVL, we set up the equation:
12V - V - 6V = 0
Now, we can solve for the unknown voltage 'V':
V = 12V - 6V = 6V
So, the voltage drop across the 4-ohm resistor is 6V.
By using KVL and following these steps, you can find unknown voltages in a series circuit by setting up and solving equations based on the voltages around a closed loop.
Jewish Law and Shavuot: What You Need to Know
You may want to see also
Frequently asked questions
Kirchhoff's Voltage Law (KVL) is a principle that states that the "algebraic sum of all voltages in a loop must equal zero". In other words, the sum of the voltage rises around a closed loop must equal the sum of the voltage drops around the loop.
To apply KVL to a series circuit, you start by assuming a direction of current flow through the circuit. This direction doesn't need to be correct, but it is desirable. Next, you assign polarities of voltages to all the resistors through which the current flows. Then, you place the correct polarities on any sources included in the circuit. Starting at any point in the circuit, you trace a closed loop in a chosen direction, noting the amount and polarity of the voltage across each component in succession. Finally, you place these voltages, with their polarities, into an equation and solve for the desired quantity.
Kirchhoff's Voltage Law, along with his Current Law, forms the basis for analysing lumped parameter circuits. These laws, along with the voltage-current characteristics of the circuit elements, enable us to systematically analyse any electrical network. KVL is particularly useful for series circuits, as they also act as voltage dividers.