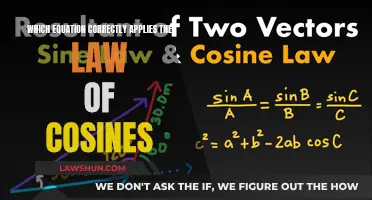
The law of sines, also known as the sine rule, is a formula used to find unknown angles and sides in triangles. The formula is:
a/sin A = b/sin B = c/sin C
Where a, b, and c are the lengths of the sides of a triangle, and A, B, and C are the opposite angles. The law of sines is one of the most useful tools in trigonometry, allowing us to make calculations based on the angles of triangles rather than their sides.
| Characteristics | Values |
|---|---|
| What is it? | An equation relating the lengths of the sides of any triangle to the sines of its angles. |
| When to use it | When two sides and the angle opposite one of them are specified, or when two sides and one non-enclosed angle are known. |
| What it can be used for | Finding unknown sides and angles. |
| Other names | Sine Rule, Sine Formula, Sine Law. |
What You'll Learn

Finding unknown sides
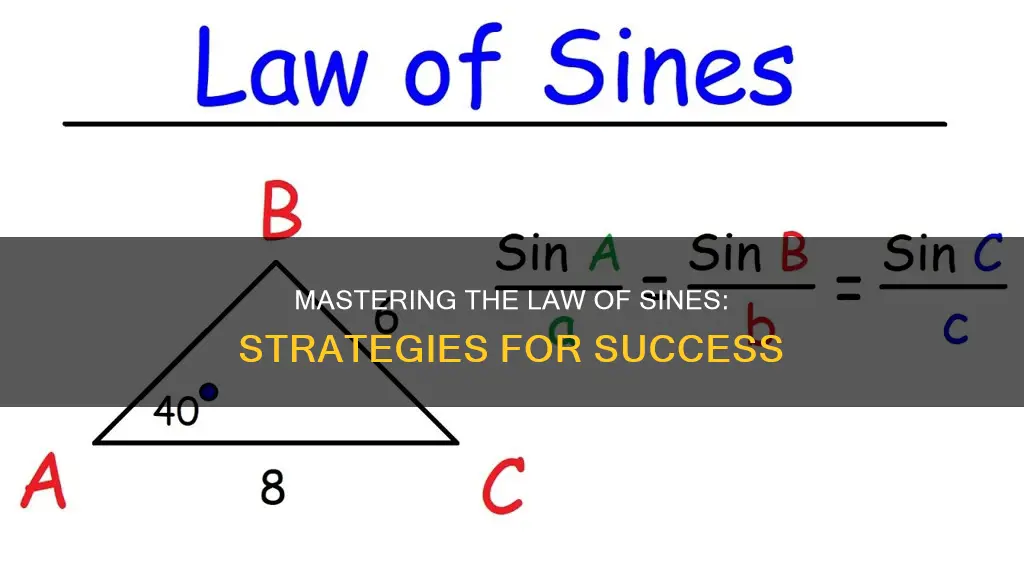
The Law of Sines, or Sine Rule, is a formula that relates the lengths of the sides of any triangle to the sines of its angles.
The formula is:
For finding unknown sides:
A/sin A = b/sin B = c/sin C
Where:
- A, b, and c are the lengths of the sides of a triangle
- A, B, and C are the angles
- A is the side across from angle A, b is across from angle B, and c is across from angle C
Example:
Calculate side "c"
A/sin A = b/sin B = c/sin C
Put in the values we know: a/sin A = 7/sin(35°) = c/sin(105°)
Ignore a/sin A (it's not useful to us): 7/sin(35°) = c/sin(105°)
Now, rearrange and solve: c/sin(105°) = 7/sin(35°)
Multiply both sides by sin(105°): c = (7 / sin(35°)) x sin(105°)
Calculate: c = (7 / 0.574...) x 0.966...
C = 11.8 (to 1 decimal place)
The Law of Sines can be used to find unknown sides when two angles and one side are known, or when two sides and one non-enclosed angle are known.
It's important to note that in some cases, the triangle is not uniquely determined by this data, leading to an ambiguous case with two possible solutions. This occurs when:
- The only information known about the triangle is angle α and sides a and c
- Angle α is acute (less than 90°)
- Side a is shorter than side c
- Side a is longer than the altitude h from angle β, where h = c sin α
The Law of Definite Composition: Elements' Essential Rule
You may want to see also

Finding unknown angles
The Law of Sines is a useful formula that can be applied to any triangle, not just a right triangle. It can be used to find an unknown angle or an unknown side of a triangle.
The Law of Sines states that:
> If a, b and c are the lengths of the legs of a triangle opposite to the angles A, B and C respectively; then the law of sines states:
>
> a/sin(A) = b/sin(B) = c/sin(C)
This can be rearranged to solve for any unknown angle or side. For example, to find angle A, the formula becomes:
> A = sin^-1 [ a * sin(B) / b]
To find an unknown angle, follow these steps:
- Substitute the known values into the formula.
- Remove the fraction that is unhelpful.
- Solve the remaining equation.
For example, if we are given a triangle with sides measuring 4 in, 5 in, and 3 cm, and we want to find angle B, we would substitute the given information into the Law of Sines formula:
> sin(B)/5 = sin(A)/4
We can then eliminate the unhelpful fraction, leaving us with:
> sin(B) = (sin(A) * 5)/4
Finally, we can solve for B by cross-multiplying and solving the equation.
The Law of Sines can also be used to calculate unknown sides of a triangle. To do this, simply enter the opposite angle and another angle-side pair, such as the angle A and side a, or angle C and side c.
Antitrust Laws: Private Companies and Legal Boundaries
You may want to see also

Using the Sine Rule
The Sine Rule, also known as the law of sines, is a rule of trigonometry that relates the sides of a triangle and its angle measurements. It can be used to find the unknown angle or side of an oblique triangle (a triangle that is not right-angled). The rule is as follows:
The Law of Sines Formula
The law of sines formula is used for relating the lengths of the sides of a triangle to the sines of consecutive angles. It is the ratio of the length of the side of the triangle to the sine of the angle thus formed between the other two remaining sides. The formula is:
A/*sin A = b/*sin B = c/*sin C
Where:
- A, b, and c are the lengths of the sides of a triangle
- A, B, and C are the angles of the triangle
This formula can be represented in three different forms:
A/*sin A = b/*sin B = c/*sin C
Sin A/a = sin B/b = sin C/c
A/b = sin A/sin B; a/c = sin A/sin C; b/c = sin B/sin C
To use the Sine Rule, you must know the measurements of at least two angles and one side, or two sides and one angle. In either case, you must have at least one pair that consists of a side and its opposite angle.
For example, the following combinations would be sufficient for the law of sines to apply:
- Side A, Side B and angle α
- Side A, Side C, and angle γ
- Sides B and C, and angle α
The following combinations are examples that would NOT be sufficient to apply the law of sines:
- Side A, Side B and Side C (this doesn't work because there are no angle measurements)
- Side A, Side B and angle γ (this doesn't work because the known angle is not opposite either of the known sides)
- Sides A and B, and angle γ (this doesn't work because the known side is not opposite either of the known angles)
Once you have the required information, you can use the law of sines to find the unknown angle or side. For example, if you know sides A and B and angle α, then you need the portion of the law of sines that says:
A/*sin α = B/*sin β
You can then fill in the numbers that you know and rearrange the equation to solve for the unknown information.
The Sine Rule can also be used to find the unknown angle or side of a right-angled triangle.
Understanding Photo Copyright Laws and Their Applications
You may want to see also

Finding the area of a triangle
The law of sines, also known as the sine rule, defines the ratio of sides of a triangle and their respective sine angles. It is used to find the unknown angle or side of an oblique triangle (any triangle that is not a right triangle).
The law of sines is defined as the ratio of side length to the sine of the opposite angle. It holds for all three sides of a triangle, regardless of their sides and angles. The formula is:
\begin{equation*}
\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}
\end{equation*}
This can also be written as:
\begin{equation*}
\sin A/a = \sin B/b = \sin C/c
\end{equation*}
The law of sines can be used to find the area of a triangle. The general formula for the area of a triangle is:
\begin{equation*}
\text{Area} = \frac{1}{2} \times \text{base} \times \text{height}
\end{equation*}
Using the law of sines, we can express the height of the triangle in terms of the sine of one of its angles. Let's assume we have a right triangle with sides a, b, and c, and angles A, B, and C. The height, h, of the triangle can be expressed as b sin C. Substituting this expression into the general formula for the area of a triangle, we get:
\begin{equation*}
\text{Area} = \frac{1}{2} \times ab \sin C
\end{equation*}
This formula allows us to find the area of a triangle without having to rely on finding the altitude (height) of the triangle. Instead, we can use this formula when we know two sides and the included angle of the triangle.
For example, let's say we have a triangle with sides a = 7 cm, b = ?, and angle A = 60°. Using the law of sines, we can find the length of side b:
\begin{equation*}
\frac{7}{\sin 60^{\circ}} = \frac{b}{\sin 45^{\circ}}
\end{equation*}
Solving for b, we get:
\begin{equation*}
B = \frac{7 \times \sin 45^{\circ}}{\sin 60^{\circ}} \approx 14/\sqrt{6} \ \text{cm}
\end{equation*}
Now that we have the lengths of two sides and the measure of the included angle, we can use the formula for the area of the triangle:
\begin{equation*}
\text{Area} = \frac{1}{2} \times ab \sin C \approx \frac{1}{2} \times 7 \times \frac{14}{\sqrt{6}} \times \sin 60^{\circ} \approx \text{34.64 cm}^2
\end{equation*}
So, the area of the triangle is approximately 34.64 square centimetres.
Applying De Morgan's Law to Gates: A Comprehensive Guide
You may want to see also

Application to vector quantities
The law of sines is used to find the angles of a triangle. When used in conjunction with the law of cosines, it can help find the third side of a triangle when two sides and the angle opposite one of them are known.
The law of sines can be applied to vector quantities in the following ways:
- Finding the difference between two vectors: The law of cosines can be used to find the difference between two vectors, as in the case of a glancing collision.
- Calculating the heading angle of an aircraft: The law of sines and the law of cosines can be used together to calculate the heading angle of an aircraft in the wind. By finding the difference between the wind direction and the desired bearing, the offset angle for the aircraft can be obtained using the law of sines. Then, the law of cosines can be applied to calculate the resultant ground speed.
- Solving complex problems: The laws of sines and cosines can be used to solve complex problems involving vectors, such as calculating the total distance travelled by a boat with a strong wind blowing at a specific angle.
Strategies for Securing 3L Big Law Positions
You may want to see also