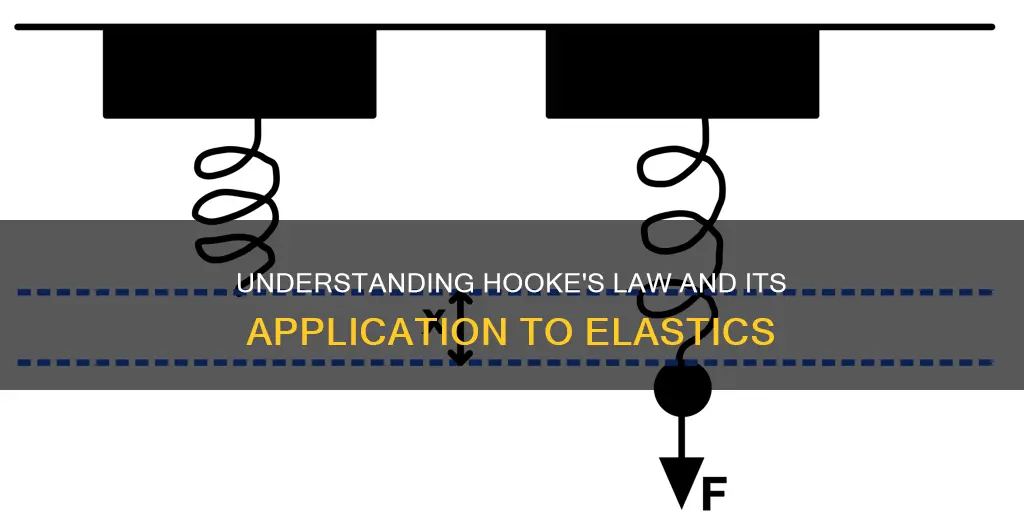
Hooke's Law, also known as the law of elasticity, was discovered by English scientist Robert Hooke in 1660. It states that the force required to extend or compress a spring is directly proportional to the resulting extension or compression. This principle can be applied to any elastic object, and is used extensively in the fields of science and engineering.
| Characteristics | Values |
|---|---|
| Named After | 17th-century British physicist Robert Hooke |
| First Stated | 1660, as a Latin anagram |
| Published Solution | 1678, as "ut tensio, sic vis" ("as the extension, so the force" or "the extension is proportional to the force") |
| Equation | F = kx |
| F | Force |
| k | Spring constant |
| x | Displacement |
| Compatibility with Newton's Laws | Compatible with Newton's laws of static equilibrium |
| Scope | Applicable to any elastic object of arbitrary complexity |
| Disadvantages | Only applies within the elastic limit of a material |
| Only accurate for solid bodies if the forces and deformations are small | |
| Not a universal principle |
What You'll Learn

Hooke's Law and Elasticity
Hooke's Law, also referred to as the law of elasticity, was formulated by 17th-century British physicist Robert Hooke. Hooke's Law is a principle of physics that states that the force required to extend or compress a spring is proportional to the distance of that extension or compression. This can be expressed as:
F = kx
Where F is the force, and x is the displacement, and k is the spring constant, or the stiffness of the spring.
Hooke's Law is a linear relationship, and it only applies within the elastic limit of the material. The elastic limit is the maximum amount a material can be stretched or compressed before it reaches plastic deformation and does not return to its original shape.
Hooke's Law is a useful approximation for solid bodies, as long as the forces and deformations are small. It is used extensively in science and engineering, and is the foundation of disciplines such as seismology, molecular mechanics, and acoustics.
Elasticity is the property of an object to return to its original shape after experiencing some form of distortion. This ability to return to its original shape is known as a "restoring force", and Hooke's Law explains that this force is proportional to the amount of stretch experienced.
Hooke's Law applies to many situations where an elastic body is deformed, such as a guitar string being plucked, or wind blowing on a tall building. It also applies to materials other than springs, such as rubber blocks, which can be deformed by shearing.
Limitations of Hooke's Law
Hooke's Law only applies within a limited frame of reference. It does not apply beyond the elastic limit of a material, and many materials will deviate from Hooke's Law before that limit is reached. It is also not a universal principle and only applies when the amount of stretch or compression is relatively small.
Applications of Hooke's Law
Hooke's Law is applied in many everyday situations, especially in the use of springs, which are used in engineering and medical science. It is also used in car suspension systems, breathing (lungs), skin, spring beds, and diving boards.
Hooke's Law is a fundamental principle of physics that explains the relationship between force and displacement for elastic objects. It has many practical applications and is essential for understanding the behaviour of elastic materials.
Does God Contradict the Law of Noncontradiction?
You may want to see also

Hooke's Law and Stress-Strain Relationship
Hooke's Law, also known as the law of elasticity, was formulated by English scientist Robert Hooke in the 17th century. Hooke's Law states that the force required to extend or compress a spring is directly proportional to the resulting extension or compression. This principle can be applied to any elastic object, and it is expressed mathematically as:
F=kx
Where:
- F is the force
- K is the spring constant (a measure of stiffness)
- X is the displacement or change in length
Hooke's Law can be understood as a special case of the stress-strain relationship. Stress refers to the force acting on a unit area within a material, and it is caused by an externally applied force. Strain is the resulting deformation produced by stress. For small deformations, Hooke's Law states that stress and strain are directly proportional to each other. This means that the material behaves elastically, and it will return to its original shape once the load is removed.
The stress-strain relationship can be expressed mathematically as:
Stress = Young's Modulus of Elasticity x Strain
Here, Young's Modulus of Elasticity (also known as the modulus of elasticity) is a property of the material and depends on its dimensions and shape.
Hooke's Law is a fundamental principle in several fields, including engineering, seismology, molecular mechanics, and acoustics. It is also applied in everyday objects such as springs, breathing lungs, skin, spring beds, diving boards, and car suspension systems.
However, it is important to note that Hooke's Law has limitations. It only applies within the elastic limit of a material and for small deformations. Once the forces exceed a certain threshold, the material may undergo permanent deformation or a change of state, and Hooke's Law will no longer hold true.
Thermodynamics Laws: Governing Energy Conversions and Efficiency
You may want to see also

Hooke's Law and Springs
Springs are a marvel of human engineering, with many varieties serving different functions, such as compression, extension, and torsion springs. The applications of springs are extensive, from automotive suspension systems to watches and clocks. Understanding the laws of elasticity, torsion, and force is essential before putting springs to use, and these laws are collectively known as Hooke's Law.
Hooke's Law is a principle of physics that describes the relationship between the force applied to a spring and its subsequent displacement. It was formulated by 17th-century British physicist Robert Hooke, who first stated the law in 1660 as a Latin anagram and later published the solution in 1678 as "ut tensio, sic vis," which translates to "as the extension, so the force" or "the extension is proportional to the force."
Mathematically, Hooke's Law can be expressed as F = -kX, where F is the force applied to the spring, X is the displacement of the spring, and k is the spring constant, indicating its stiffness. This law applies when the deformation and stress on an elastic object can be expressed by a single number, which can be either positive or negative.
The law is not universally applicable and has certain limitations. It only holds true for solid bodies when the forces and deformations are small. Additionally, Hooke's Law fails beyond the elastic limit of a material, and many materials may deviate from it even before reaching that limit.
Despite its limitations, Hooke's Law is a valuable tool in various fields. It is extensively used in science and engineering and serves as the foundation for disciplines such as seismology, molecular mechanics, and acoustics. It is also essential in creating devices like the spring scale, manometer, and the balance wheel of a mechanical clock.
Suppressor Self-Manufacture: Legal or Not?
You may want to see also

Hooke's Law and Elastic Limit
Hooke's Law, also known as the law of elasticity, was formulated by English scientist Robert Hooke in the 17th century. Hooke's Law states that the force required to extend or compress a spring is directly proportional to the displacement of the spring. This relationship can be expressed by the equation:
F = kx
Where F is the force applied, x is the displacement, and k is the spring constant. The spring constant represents the stiffness of the spring and depends on the material and shape of the spring.
Hooke's Law applies to a wide range of situations beyond just springs, including any instance where an elastic body is deformed. For example, it can be applied to a balloon being inflated, a rubber band being stretched, or a building swaying in the wind.
However, Hooke's Law only holds true within the elastic limit of the material. The elastic limit is the maximum amount a material can be stretched or compressed before it deviates from Hooke's Law and experiences permanent deformation or a change of state. Many materials will start to deviate from Hooke's Law well before reaching their elastic limits.
Hooke's Law is a foundational principle in several fields, including seismology, acoustics, and molecular mechanics. It is also essential for understanding the behaviour of elastic materials and has practical applications in engineering and everyday life.
US Law and International Students: What's the Deal?
You may want to see also

Applications of Hooke's Law
Hooke's Law, discovered by English scientist Robert Hooke in 1660, has a wide range of applications in various fields. Here are some examples of how Hooke's Law is applied in everyday life and different areas of science and engineering:
Everyday Applications
- Spring-based Shock Absorbers: In automotive suspension systems, coil springs are used to absorb shocks and vibrations from the road. According to Hooke's Law, the force applied by the spring is directly proportional to the displacement, allowing the vehicle to maintain a smooth and controlled ride.
- Mechanical Watches and Clocks: The balance wheel in watches and clocks is fitted with a balance spring or hairspring, typically made of highly elastic material. As the balance wheel oscillates, the spring stretches and contracts, applying a restoring force in accordance with Hooke's Law, ensuring precise and timely timekeeping.
- Sports Equipment: Trampolines utilize Hooke's Law to provide elasticity and bounce. The trampoline's surface, made of stretchable fabric or synthetic material, is supported by coiled springs. When someone jumps on the trampoline, the springs distort, absorbing and releasing the jumper's kinetic energy, resulting in an enjoyable bouncing experience.
- Breathing, Skin, Spring Beds, Diving Boards, and Car Suspension Systems: Hooke's Law is relevant in understanding the behaviour of elastic materials in these everyday objects and body functions.
Scientific and Engineering Applications
- Seismology, Acoustics, and Molecular Mechanics: Hooke's Law serves as the foundation for these scientific disciplines, helping us understand the behaviour of elastic materials and the relationship between stress and strain.
- Manometer, Spring Scale, and Balance Wheel of a Clock: Hooke's Law is the fundamental principle behind these devices, ensuring accurate measurements and precise timekeeping.
- Elasticity and Restoring Force: Hooke's Law describes the property of elasticity, which is the tendency of an object to return to its original shape after distortion. This "restoring force" is proportional to the stretch experienced, as explained by Hooke's Law.
- Engineering and Construction: Hooke's Law is crucial for understanding the strength and behaviour of materials used in various engineering and construction projects.
- Understanding Stretchy Objects: Hooke's Law helps us predict how stretchy objects will behave when compressed or extended, making it valuable for designing and working with elastic materials.
Coulomb's Law: Understanding IMS Interactions
You may want to see also
Frequently asked questions
Hooke's Law is a principle of physics that states that the force required to extend or compress a spring is proportional to the distance of that extension or compression.
The equation for Hooke's Law is F = kx, where F is the force, and x is the displacement or change in length. k is a constant factor known as the spring constant.
Hooke's Law is significant as it helps us understand how elastic objects behave when stretched or compressed. It also serves as the foundation for many scientific disciplines, such as seismology, acoustics, and molecular mechanics.
Hooke's Law only applies within a limited frame of reference. It does not hold true when the forces exceed a certain limit, and the material reaches its minimum compression or maximum stretch. Additionally, it is accurate only for solid bodies and small forces and deformations.
Hooke's Law is applied in various everyday objects, such as springs, breathing lungs, skin, spring beds, diving boards, car suspension systems, and musical instruments like guitars.







